3.2. Моделирование производных случайных последовательностей с заданным законом распределения

В основу моделирования производных случайных последовательностей положен метод обратной функции, основная идея которого заключается в следующем.

Как известно, под интегральным законом распределения случайного процесса понимается вероятность появления его значений в интервале . При этом отыскание значения случайного процесса , соответствующего заданной величине вероятности , может быть произведено по формуле:

, (8)

где – функция, обратная функции (рис.4).

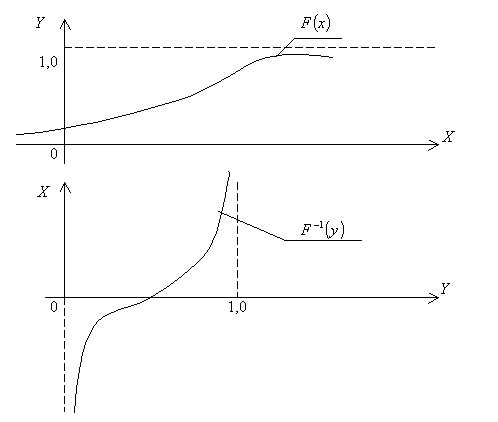
Суть моделирования случайного процесса с заданным методом обрат

Суть моделирован

Рис. 4

Суть моделирования случайного процесса с заданным законом распределения методом обратной функции распределения заключается в том, что каждому значению базисной последовательности , равномерно распределенной в интервале , ставится в соответствие значение случайной последовательности , определенное по формуле:

.

Блок–схема программы, предназначенной для воспроизведения случайных последовательностей по описанным выше алгоритмам и оценки качества этого воспроизведения, приводится в следующем разделе данных методических указаний.

3.3. Блок–схема подпрограммы воспроизведения псевдослучайных последовательностей с заданными свойствами.

. БЛОК–СХЕМА ПРОГРАММЫ ВОСПРОИЗВЕДЕНИЯ ПСЕВДОЫХ ОВАТЕЛЬНОСТЕЙ

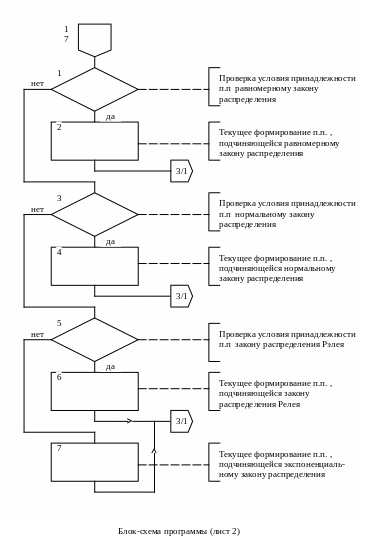
Блок-схема программы (лист 2)

3.4. Контроль и оценка качества имитируемых псевдослучайных последовательностей на эвм

Оценка качества воспроизведения псевдослучайной последовательности может производиться путем сравнения статистических характеристик получаемого процесса и процесса, подлежащего имитации (заданного). В данной курсовой работе в качестве таких характеристик используются математическое ожидание, дисперсия и дифференциальный закон распределения (гистограмма).

Вычисление оценок математического ожидания и дисперсии воспроизведенной псевдослучайной последовательности производится по формулам:

,

(9)

.

Для построения гистограммы производится переход от смоделированной случайной последовательности к последовательности

.

Область определения функции плотности вероятностей этой последовательности , где под и понимаются ее минимальное и максимальное значения, подразделяется на ряд равновеликих интервалов

.

Под значением ординаты гистограммы , соответствующей –тому из указанных интервалов, принимается отношение числа узлов псевдослучайной последовательности , попавших в этот интервал, к произведению , т.е.

Плотность вероятностей процесса, подлежащего воспроизведению, считается заданной, а соответствующее ей математическое ожидание и вычисляются по формулам:

, (10)

. (11)

Контроль точности воспроизведения имитируемого случайного процесса может быть произведен по формулам:

, (12)

, , (13)

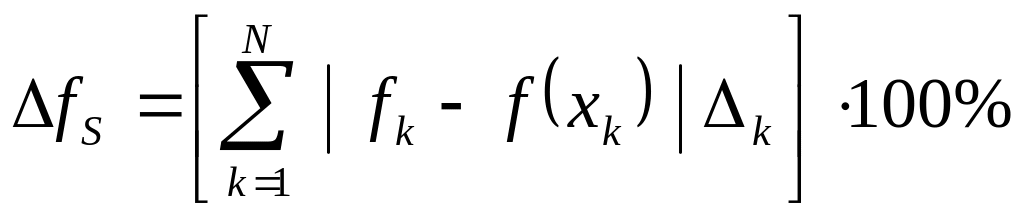. (14)

где под понимается координата середины интервала , а под – среднеинтегральное рассогласование между гистограммой и теоретической функцией плотности вероятностей.