
Краткая теория
Теоретический
анализ броуновского движения, произведённый
Смолуховским и Эйнштейном, показал, что
целесообразно находить на опыте средние
квадратичные смещения
![]() броуновских частиц или их проекции
броуновских частиц или их проекции
![]() на какое-нибудь произвольное направление
х. Чертой сверху мы обозначим операцию
усреднения величины
на какое-нибудь произвольное направление
х. Чертой сверху мы обозначим операцию
усреднения величины
![]() по многим её значениям, измеренным через
равные промежутки времени
по многим её значениям, измеренным через
равные промежутки времени
![]() .
В результате полной беспорядочности
теплового движения частиц среднее
значение величины
.
В результате полной беспорядочности
теплового движения частиц среднее
значение величины
![]() равно нулю.
равно нулю.
Оказывается, что для случая беспорядочного теплового движения частиц связь этих величин с промежутками времени , в течение которых происходили смещения , очень проста. Именно
= 2D , (1)
где D — коэффициент диффузии частицы в жидкости или в газе. Полученные на опыте многочисленные подтверждения этого соотношения явились доказательством молекулярно-кинетической природы броуновского движения. Изучение броуновского движения послужило основанием к исследованиям в дальнейшем ряда флуктуационных явлений.
Рассмотрим принадлежащий А.Эйнштейну элементарный вывод соотношения (1), экспериментальная проверка справедливости которого составляет предмет данной задачи.
 Пусть
в некотором объёме однородной жидкости
или газа находятся посторонние взвешенные
частицы или молекулы и концентрация их
меняется только в направлении некоторой
координаты х. Обозначим их концентрацию
(число частиц в единице объёма) буквой
n.
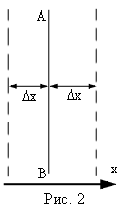
Проведём мысленно плоскость АВ
перпендикулярно к оси х
(рис. 2).
Пусть
в некотором объёме однородной жидкости
или газа находятся посторонние взвешенные
частицы или молекулы и концентрация их
меняется только в направлении некоторой
координаты х. Обозначим их концентрацию
(число частиц в единице объёма) буквой
n.
Проведём мысленно плоскость АВ
перпендикулярно к оси х
(рис. 2).
В результате
теплового движения частицы будут
изменять свою координату х,
причём смещения частиц в направлении
+х и
–х будут
равновероятны. Пусть среднее квадратичное
смещение частицы вдоль оси х
за время
будет
![]() .
В таком случае не представляет труда
подсчитать поток частиц, который за
время
продиффундирует сквозь плоскость АВ.
Если
концентрация частиц влево от плоскости
в среднем на отрезке
будет
.
В таком случае не представляет труда
подсчитать поток частиц, который за
время
продиффундирует сквозь плоскость АВ.
Если
концентрация частиц влево от плоскости
в среднем на отрезке
будет
![]() ,
а вправо от плоскости — соответственно
,
а вправо от плоскости — соответственно
![]() ,
то искомый поток частиц N
за время
через 1 см2
нашей
плоскости слева направо выразится
соотношением
,
то искомый поток частиц N
за время
через 1 см2
нашей
плоскости слева направо выразится
соотношением
![]() .
(2)
.
(2)
С другой стороны, макроскопическое изучение диффузии показывает, что число продиффундировавших через 1 м2 плоскости частиц N за время пропорционально градиенту концентрации диффундировавшего вещества и времени , т.е. можно записать
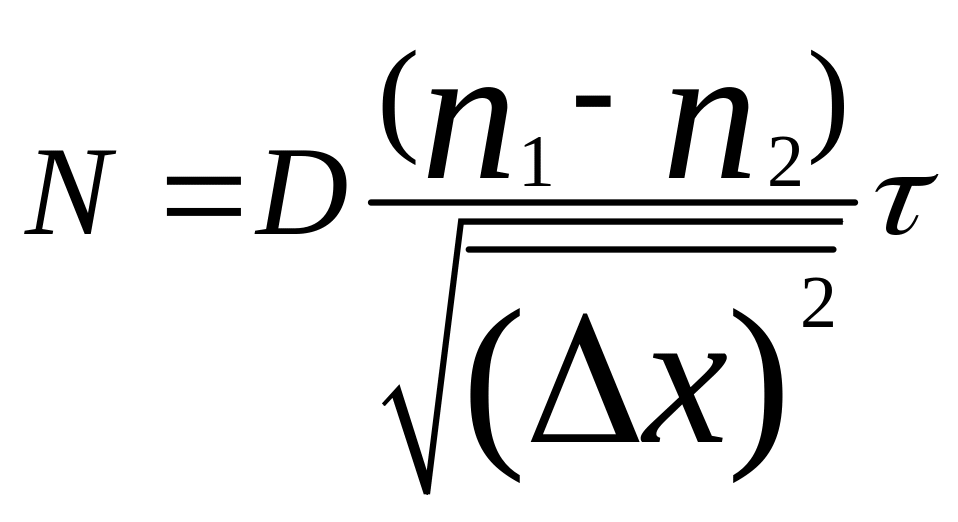 ,
(3)
,
(3)
где D — коэффициент диффузии. Размерность коэффициента диффузии м2/с, а его физический смысл таков: это — количество вещества (частиц), прошедшее через 1 м2 плоскости АВ в 1 с при градиенте концентрации частиц, равном единице.
Приравнивая друг другу полученные выражения для N, находим
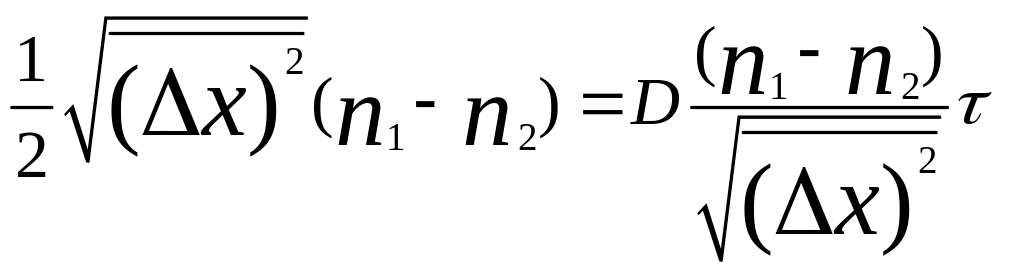 ,
,
откуда получается искомое соотношение
= 2D .
Хотя проведённый нами расчёт и опирался на рассмотрение процесса диффузии, однако полученный результат для связи между и временем не зависит от числа диффундировавших частиц, а следовательно, он справедлив и для перемещений отдельной броуновской частицы.
Если частицы имеют сферическую форму, то формула Смолуховского-Эйнштейна может быть представлена в виде
![]() ,
(4)
,
(4)
где R — универсальная газовая постоянная,
Т — абсолютная температура,
![]() — коэффициент
вязкости среды,
— коэффициент
вязкости среды,
r — радиус частицы,
NA — постоянная Авогадро,
— величина промежутка времени, за который происходит перемещение частицы.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
На рис. 3 изображён микроскоп с камерой для визуального наблюдения броуновского движения частиц дыма:
1 — окуляр;
— окуляр;
2 — объектив;
3 — камера для дыма;
4 — винт грубой наводки на резкость;
5 — винт тонкой наводки на резкость.
Наблюдательная камера, наполненная дымом, (рис.3) помещается на столик микроскопа, так, чтобы удобно было использовать объектив с небольшим увеличением. Рядом с микроскопом ставится источник света – проектор, подсвечивающий дым в камере. Окуляр микроскопа при необходимости может быть заменён web-камерой на микрофотонасадке.
ИЗМЕРЕНИЯ
Упражнение 1. Рис. 3. Микроскоп с камерой для дыма
Пучок света от осветителя направьте так, чтобы свет проходил через оба окна камеры. С одного из штуцеров камеры снимите трубку-заглушку и с помощью шприца с иглой вдуйте через штуцер в камеру дым от ароматизированной палочки, после чего наденьте на штуцер заглушку. Перед наблюдением в отражённом свете необходимо некоторое время выждать, чтобы успокоилось турбулентное движение частиц дыма, возникшее в процессе вдувания.
Частицы дыма под действием ударов молекул воздуха приходят в беспорядочное броуновское движение, которое и наблюдается в микроскоп.
Запишите результаты наблюдения.
Упражнение 2.
На столик микроскопа поместите предметное стекло с лункой, которая заполнена сильно разбавленным молоком. Осторожно накройте лунку покровным стеклом. Толщина этого стекла около 0.1 мм, поэтому соблюдайте особую осторожность при обращении с ним!
Наблюдение проводите в проходящем свете, для чего на микроскопе включите тумблер его осветителя. С помощью винтов микроскопа 4 и 5 аккуратно сфокусируйте микроскоп на шариках жира, поле зрения в окуляре при этом не должно быть очень ярким. Перед наблюдением необходимо некоторое время выждать, чтобы успокоилось направленное движение броуновских частиц, возникшее из-за того, что столик микроскопа расположен не горизонтально. При наблюдении не следует облокачиваться на стол, на котором стоит микроскоп.
Наблюдайте за движением этих частиц. Шарики жира имеют различные размеры. Запишите наблюдаемую разницу в их движениях. Проведите наблюдение с другим объективом.
Упражнение 3
Замените окуляр микроскопа web-камерой на микрофотонасадке. Осторожно разместите на ровном участке предметного стекла объект-микрометр — стеклянную пластинку с делениями: 100 делений на 10 мм и получите чёткое их изображение. Измерьте миллиметровой линейкой на экране монитора наименьшее расстояние между делениями объект-микрометра и вычислите увеличение микроскопа. Запишите его.
Упражнение 4.
П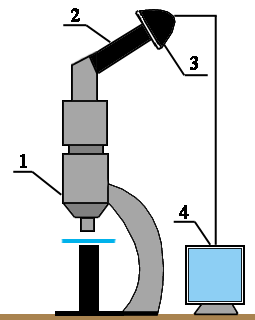 оместите
под объектив микроскопа область
предметного стекла с препаратом. На
экране монитора наблюдайте броуновское
движение частиц (рис.4). Система микроскопа
вполне подготовлена к наблюдениям,
возможно, понадобится только немного
подфокусировать изображение броуновских
частиц на экране монитора вращением
ручки тонкой фокусировки микроскопа.
Следует иметь в виду, что различные
частицы расположены на разных уровнях.
оместите
под объектив микроскопа область
предметного стекла с препаратом. На
экране монитора наблюдайте броуновское
движение частиц (рис.4). Система микроскопа
вполне подготовлена к наблюдениям,
возможно, понадобится только немного
подфокусировать изображение броуновских
частиц на экране монитора вращением
ручки тонкой фокусировки микроскопа.
Следует иметь в виду, что различные
частицы расположены на разных уровнях.
Рис. 4. Схема установки: 1 — микроскоп с препаратом; 2 — микрофотонасадка; 3 — web-камера; 4 — монитор компьютера |
Поэтому, как правило, нельзя одновременно хорошо видеть все броуновские частицы. Их надо выбирать и отдельно на них фокусировать микроскоп. |
Выполняющие упражнение должны внимательно рассмотреть движение частиц, убедиться в хаотичности их движений, в том, что маленькие частицы движутся быстрее крупных.
В опыте предстоит исследовать зависимость среднего квадрата перемещения броуновских частиц от времени их движения.
Эту часть работы необходимо проводить вдвоём. Наложите на экран монитора половину прозрачного файла. Из-за явления электризации файл будет хорошо держаться на экране. Выберите для наблюдений не очень крупную частицу и измерьте линейкой размеры её изображения, результаты измерений запишите. Один из наблюдающих должен следить за частицей и гелиевой ручкой ставить на файле точки, отмечающие положение частицы через определённые промежутки времени tизм (5 — 30) с, последовательно нумеруя эти положения (важно не перепутать последовательность точек). Второй должен «держать» частицу в фокусе и следить за временем, отдавая команды, когда необходимо ставить точки. Для одной и той же частицы надо зафиксировать не менее десяти точек. Если частица уходит из поля зрения, то для наблюдения следует выбрать другую частицу примерно тех же размеров и начать зарисовку заново. Не забудьте снова измерить размеры изображения частицы на экране монитора. Запишите температуру в помещении во время измерений.
Затем, наблюдающие меняются местами и проводят измерения для второго экспериментатора, фиксируя их на другой половине файла.
