Тема 1.5. Построить сложные таблицы по подлежащему и сказуемому

(ЗАДАЧА 1.8.).

Тема 1.6. Построить линейный график, радиальный график сезонности, знаки Варзара по урожайности и картограмму плотности населения по 5 районам области

(ЗАДАЧА 1.9. )

Тема 1.7. Вариации в массовых явлениях.

ЗАДАЧА 1.10. Расчет квартилей распределения.

Дано: По данным статистического наблюдения о периоде функционирования (х_i - лет) 100 банков (n = 100) построен ранжированный интервальный ряд распределения из 8 интервалов (длина интервала и_н = 1 год) (х_i : 1-2; 2-3; 3-4; 4-5; 5-6; 6-7; 7-8; св. 8 лет) с соответствующим количеством (частотой - f_i) банков в каждом интервале (f_i: 10; 15; 21; 25; 12; 7; 5; 5 банков) и накопленной частотой (кумулятой – S_i) (S_i : 10; 25; 46; 71; 83; 90; 100 банков). При разделении всей совокупности банков на 4 равные части номер 2-го квартиля (Q₂) равен N_Q2 = [(100+1) / 4] * 3 = 50,5 ( который находится в объеме кумуляты S_Q4 = 71 4-го интервала c пределами х_i = 4 - 5 лет).

Номер 3-го квартиля (Q₃) равен N_Q3 = [(100+1) / 4] * 3 = 75,75 ( который находится в объеме кумуляты S_Q5 = 83 5-го интервала c пределами х_i = 5 - 6 лет).

(К_в = N_сп ; f_{i вар} = f_i + К_в ). Определить: Величину 2-го и 3-го квартилей.

Решение: Общая фрмула расчета i-го квантиля при разделении совокупности на j равных частей имеет вид: Q_ij = х _{min Qij} + и_н * (∑ f i * j / к – S _{Qij – 1} ) / f _Qij;

1. Второй квартиль или Медиана (Ме): Q₂ = х _{min Q2} + и_н * (∑ f i * 2 /4 – S _{Q2 – 1} ) /f_Q2) = 4 + 1 *[ (100 * 2 /4) - 46]/25 =4 + (4/25) = 4 + 0,16 = 4,16 г.

2. Третий квартиль: Q₃ = х _{min Q3} + и_н * (∑ f i * 3 /4 – S _{Q3 – 1} ) / f_Q3) = 5 + 1 *[ (100 * 3 /4) - 71]/12 =5,33 г.

Выводы:

1. Первые 50% банков (первая половина) имеет средний «срок жизни» (жизненный цикл - ЖЦ) 4,16 г и менее, вторая половина банков имеет ЖЦ более 4,16 г.

2. 75% банков (первые 3/4) имеет ЖЦ 5,3 г. и менее, а последние 25% банков имеет ЖЦ более 5,33 г.

Тема 1.8. Расчет показателей вариации.

ЗАДАЧА 1.11. Расчет показателей вариации. Построение графиков рядов распределения.

Дано: Имеются данные статистического наблюдения об объемах реализации продукции (не ранжированный ряд Q_piнр = х_iнр, млн. руб., табл. 1, гр. 2) на конец года по 20 предприятиям города (i = 1,n; n = 20).

Необходимо: 1) Определить показатели вариации ряда распределения предприятий по объему реализованной продукции и сделать выводы. Данные статистического наблюдения и результаты статистической сводки и группировки оформить статистическими таблицами и графиками.

2) Ранжировать исходный ряд распределения по рангу возрастания величины признака (Qi_р = x_ip табл.1, гр.3).

3) Рассчитать и построить группы и интервалы (табл.1, стр.4) распределения (при Кгр = 4) и определить частоты (f i) по интервалам (табл.1, стр. 5).

4) Построить сложную (по подлежащему) таблицу (табл.2)

5) Рассчитать показатели вариации: R_в– размах вариации; d_ср – среднее линейное отклонение; σ² – дисперсию; σ - среднее квадратическое отклонение; К _осц - коэффициент осцилляции; К_dср - коэффициент среднего линейного отклонения; V _в - коэффициент вариации; М_о - моду; М_е - медиану.

6) Построить графики распределения по вариантным значениям f_i: гистограмму (Рис. – графическое изображение интервального ряда (f_i –х_i); кумуляту – графическое распределение концентрации производства (S_i - х_i); полигон распределения - графическое изображение характера (вида) кривой распределения.

№	хiнр	хiр	игр	fi	№	хiнр	хiр	игр	fi
1	2	3	4	5	1	2	3	4	5
1	4	1	1-3	f 1	11	5,8	5,7	5-7	f 3
2	2	2			12	5,7	5,8
3	1	2			13	7,5	6
4	2	3,1	3-5	f 2	14	6,3	6
5	3,1	3,4			15	6	6,2
6	4	4			16	5,4	6,3
7	3,4	4			17	9	6,4
8	6.4	4,8			18	6,2	6,8
8	4.8	5,3	5-7	f3	19	6	7,5	7-9	f 4
10	6,8	5,4			20	5.3	9

Таблица 1.3. Объем реализации продукции и группировка по интервалам

Примечание к таблице 1.3.: 1) х_min = 1 млн. руб; х_max = 9 млн. руб.; и_гр – величина группового интервала f_i - частоты распределения по интервалам;

х_iнр единицы не ранжированного ряда; - х_iр – единицы ранжированного ряда по величине признака – по объему реализованной продукции (Qi_р = x_ip ) предприятия

Решение: Расчёт и построения групп, интервалов и показателей вариации.

1) Размах вариации признака (объема реализации) R_в = х_max – х_min = 9 – 1 = 8 млн. руб. Оптимальное количество групп (формула Стеджерсса):

K_гр.опт = 1 + 3.32 * lg N (n); lg 20 = 1,3; K_гр = 1 + 3.32 * 1.3 = 5.3; принимаем K_гр = 4. Величина группового интервала: и_гр = R_в /K_гр = 8/4 =2 млн. руб.

2) Расчёт интервалов:

1. х_min1 – х_max1; х_min1 = х_min = 1 млн. руб.; х_max1 = х_min1 + и_гр = 1 + 2 =3 млн. руб.

2. х_min2 - х_max2; х_min2= х_max1=3 млн. руб.; х_max2= х_min2+и_гр=3+2=5 млн. руб.

Тоже для 3 и 4 интервала: (1-3), (3-5), (5 – 7), (7 -9) (табл. 2, гр. 2).

3)Построение аналитической таблицы и расчет ее показателей вариации.

Таблица1.4. Расчетная таблица для определения показателей вариации,млн. руб.

№ п/п	Игр	fi	Si	xiс	xiּfi	÷xi – ÷	÷xi - ÷ּfi	(xi- )2	(xi- )2* fi	Fчi %	Прi
1	2	3	4	5	6	7	8	9	10	11	12
1	1-3	3	3	2	6	(-)3	9	9	27	15	1,5
2	3-5	5	8	4	20	(-)1	5	1	5	25	2,5
3	5-7	10	18	6	60	1	10	1	10	50	5,0
4	7-9	2	20	8	16	3	6	9	18	10	1,0
-	Итог	20	-	-	102	-	30	-	60	100	-

(К_в = N_сп ; f_{i вар} = f_i + К_в )

_{ср. ариф. взвеш.}= млн. руб. Принимаем: =5 млн. руб.;

S_i - кумулята – накопленная частота (S₁=f₁=3; S₂=S₁+f₂=3+5=8 и т. д.; гр. 4);

x_{i с} – серединные значения интервалов.

4) Расчет частостей (процентное выражение частоты):

f_чi=f_чּ%_{1предпр}. Процент одного предприятия: %_{1предпр}= ;

f_ч1=f₁ּ%_{1предпр} = 3 ּ 5 = 15% и т. д. (графа 11).

5) Расчет показателей плотности распределения – количества предприятий на величину интервала:

Пр_i = ; Пр₁ = и т. д. (графа 12).

6. R _в = X_max - X_min= 9 – 1 = 8 млн. руб. 6. 2. 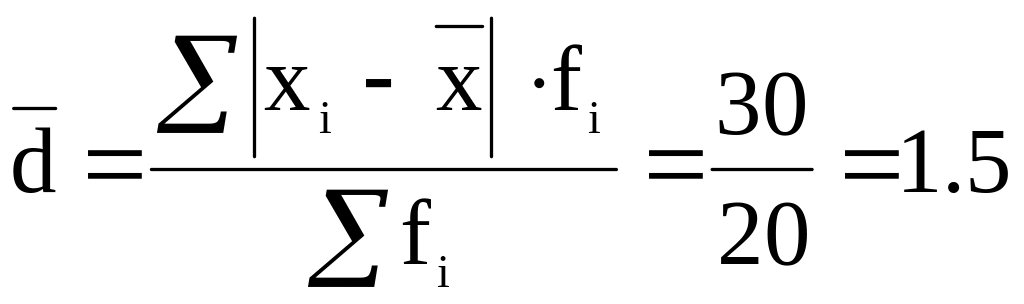млн. руб.

7) (σ²).

8) 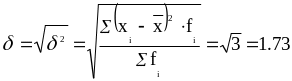млн. руб.

9) K_осц= . 9.1. .

10) Коэффициент вариации: .

V_в < 40% , следовательно, является типичной величиной распределения, отражающей основную закономерность изучаемого массового явления – распределения предприятий по объему реализации продукции.

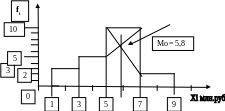
1. Рис. 1.1. Гистограмма распределения: f_i – x_i, при И_гр = 2.

Мода Мо = 5,8 млн.руб.

(Построить гистограмму по полученным индивидуальным значениям частот f_i по варианту)

11) Мода:

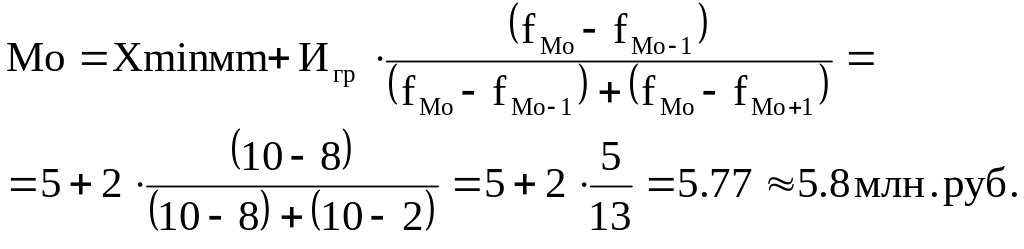
5

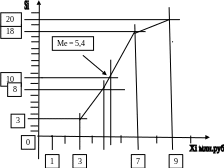
Рис. 1.2. Кумулята распределения: Si – x_i (подставить индивидуальные значения Si по концам интервалов). Медиана (Ме) – 10-я варианта в ряду распреления: Ме = 5,4 млн.руб.

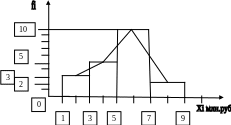
Рис.1.3. Полигон (форма) распределения: ломаная линия соединяющая середины интервалов распределения x_i на уровне частот f_i (подставить индивидуальные частоты по варианту f_{i вар})

12) Медиана: Ме = x_minМе+И_гр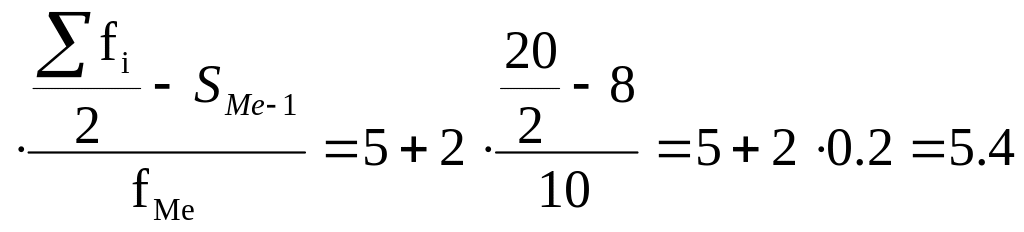 млн. руб.

Вывод: _ср=5.1< Ме=5.4< Мо=5.8.

Фактическая кривая распределения имеет асимметричный характер. Величина и знак асимметрии (смещения центра распределения) определяется по формуле: As= .Асимметрия (-) левосторонняя. (σ ).