Основные методические положения, используемые при решении задач на пересечение кривой поверхности (конуса) плоскостью

При пересечении конуса плоскостью могут быть получены следующие фигуры сечения: окружность, если секущая плоскость перпендикулярна оси вращения; эллипс, если секущая плоскость пересекает все образующие конуса; парабола, если секущая плоскость параллельна только одной образующей поверхности; гипербола, если секущая плоскость параллельна двум образующим поверхности; две прямые, если секущая плоскость проходит через вершину конуса. Простейшими сечениями конуса являются окружность и две прямые.

Если секущая плоскость проецирующая, то перечисленные фигуры сечения будут проецироваться на одну из плоскостей проекций в линию, а на вторую – в проекцию фигуры сечения. В этом случае решение задачи сводится к построению проекций ряда точек фигуры сечения конуса как точек, расположенных на образующих или направляющих линий заданного конуса.

Для решения задачи 2 требуется знать способы преобразования чертежа: замена плоскостей проекций, вращения вокруг осей, перпендикулярных плоскостям проекций, плоскопараллельного перемещения и совмещения.

При изучении способа замены плоскостей проекций необходимо иметь ввиду, что фигура не имеет своего положения в пространстве, плоскость же проекций П₁ или П₂ заменяют новой плоскостью соответственно П₅ и П₄. Такую замену проводят последовательно, сначала заменяют одну плоскость, потом другую.

При построении проекции фигуры на новой плоскости проекций необходимо помнить, что происходит переход от одного эпюра к другому, на котором соответственные проекции точек также расположены на линиях связи. Координата точки на новой плоскости проекций равна координате точки на заменяемой плоскости проекций.

При использовании способа вращения или плоскопараллельного перемещения меняется положение фигуры относительно плоскостей проекций; сами же плоскости проекций своего положения не меняют. Это приводит к построению новых проекций на тех же плоскостях. Вращение (в зависимости от характера задачи) выполняют в два этапа – вначале вращение производят вокруг одной оси, затем вокруг другой плоскости.

При вращении фигур вокруг осей, перпендикулярных плоскостям проекций, необходимо учитывать следующее:

1. Линия перемещения точки (траектория) представляет собой окружность. Так как плоскость траектории параллельна плоскости проекций, то проекции точки перемещаются: одна по окружности, другая по прямой параллельной оси проекций.

2. Горизонталь или фронталь преобразуется в прямую, перпендикулярную плоскости проекций, одним вращением.

3. Прямую общего положения можно преобразовать в прямую, перпендикулярную какой-либо плоскости проекций, в результате двух вращений: вначале вокруг одной оси, а затем вокруг второй. Эти оси взаимно перпендикулярны.

4. Проекция фигуры на ту плоскость проекций, на которой ось вращения проецируется в точку, не изменяется ни по величине, ни по форме, изменяется только её положение относительно оси проекций

5. Ось проекций не участвует в решении задач (как это имеет место при замене плоскостей проекций), поэтому на чертеже она может быть не проведена.

Применяя способ плоскопараллельного перемещения, перемещают фигуру так, что все её точки перемещаются в плоскостях, параллельных какой-либо одной плоскости проекций. Поэтому проекции траекторий точек на вторую плоскость проекций представляют собой прямые линии, параллельные оси проекций. Как при вращении вокруг осей, перпендикулярных плоскостям проекций, при плоскопараллельном перемещении одна проекция фигуры не меняется ни по величине, ни по форме.

При вращении вокруг осей, параллельных плоскостям проекций, плоскость фигуры совмещается с плоскостью, параллельной одной из плоскостей проекций. Проекция траектории точки на эту плоскость представляет собой отрезок прямой линии, перпендикулярной проекции оси вращения. При этом радиус вращения точки проецируется в натуральную величину, так как становится параллельным плоскости проекций.

В частном случае ось вращения может лежать в плоскости проекций (след плоскости).

При решении метрических задач способами преобразования проекций следует исходить из следующих основных положений:

1. Плоская фигура проецируется в натуральную величину на ту плоскость проекций, которой она параллельна;

2. Отрезок, определяющий расстояние между двумя параллельными прямыми, проецируется в натуральную величину в случае, если плоскость, в которой лежат прямые, параллельна плоскости проекций или, когда прямые перпендикулярны плоскости проекций и проецируются на эту плоскость в точки;

3. Расстояние от точки до плоскости проецируется в действительную величину на ту плоскость проекций, которой перпендикулярна заданная плоскость;

4. Спроецировать фигуру, лежащую в плоскости общего положения, в отрезок прямой линии можно одним перемещением (поворотом) или одной заменой плоскости проекций. Для этого нужно горизонталь или фронталь плоскости фигуры расположить перпендикулярно плоскости проекций или плоскость проекций расположить перпендикулярно одной из этих линий;

5. Чтобы фигура, лежащая в плоскости общего положения, стала параллельна плоскости проекций, нужно дважды переместить фигуру (повернуть её) или дважды заменить плоскость проекций. Вначале плоскость фигуры нужно сделать проецирующей, а затем параллельной плоскости проекций. Вращая фигуру вокруг оси, параллельной или лежащей в плоскости проекций (т.е. вокруг горизонтали, фронтали или одного из следов плоскости), можно найти её величину в результате одного вращения.

В решении некоторых задач возможно сочетание различных способов.

Для решения задачи 3 необходимо выполнить следующее: на ортогональном изображении конуса выбрать направления осей координат для построения аксонометрии, затем в правой половине листа вычертить аксонометрические оси координат, соответствующие изометрии (см. рис. 21), построить вторичные проекции основания конуса (эллипса) и фигуры сечения, используя при этом ортогональные проекции конуса и систему осей координат, к которой отнесён конус для построения аксонометрии. После этого для каждой точки проекции фигуры сечения откладывают их высоту и полученные точки последовательно соединяют линиями. Завершают построения вычерчиванием двух крайних образующих конуса, которые являются касательными к основанию конуса и фигуры сечения. Основной сплошной линией обводят видимый контур конуса, штриховой – невидимый, вторичные проекции и построения оставляют в тонких линиях.

Образец выполнения задачи приведён в рис.24. При этом нужно помнить о том, что окружности в аксонометрии перерождаются в эллипсы. Величины их большой и малой осей зависят от типа аксонометрии. При построении прямоугольной аксонометрии обратите внимание на то, что во всех трёх плоскостях прямоугольной изометрической и диметрической аксонометрии большая ось эллипса должна быть направлена перпендикулярно оси, отсутствующей в данной плоскости. Построение эллипса следует начинать с определения его центра, затем определить вершины эллипса (концы большой и малой осей) и четыре точки, принадлежащей диаметрам, параллельным аксонометрическим осям.

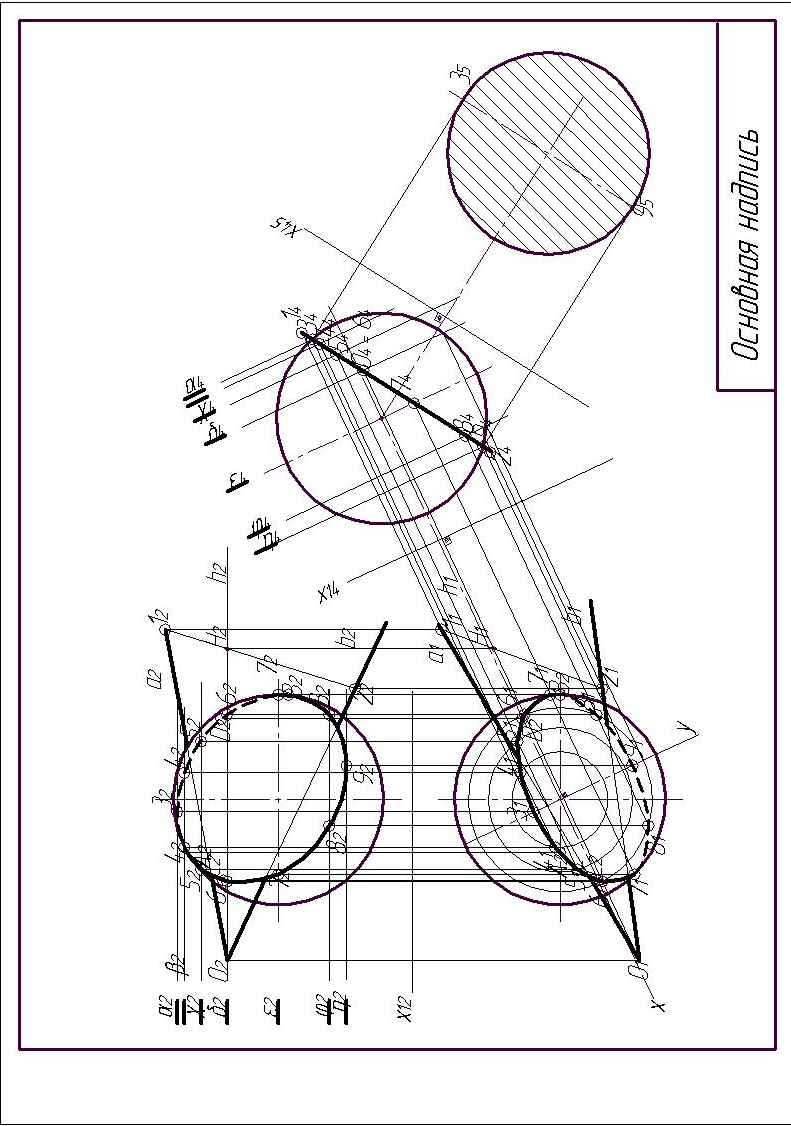
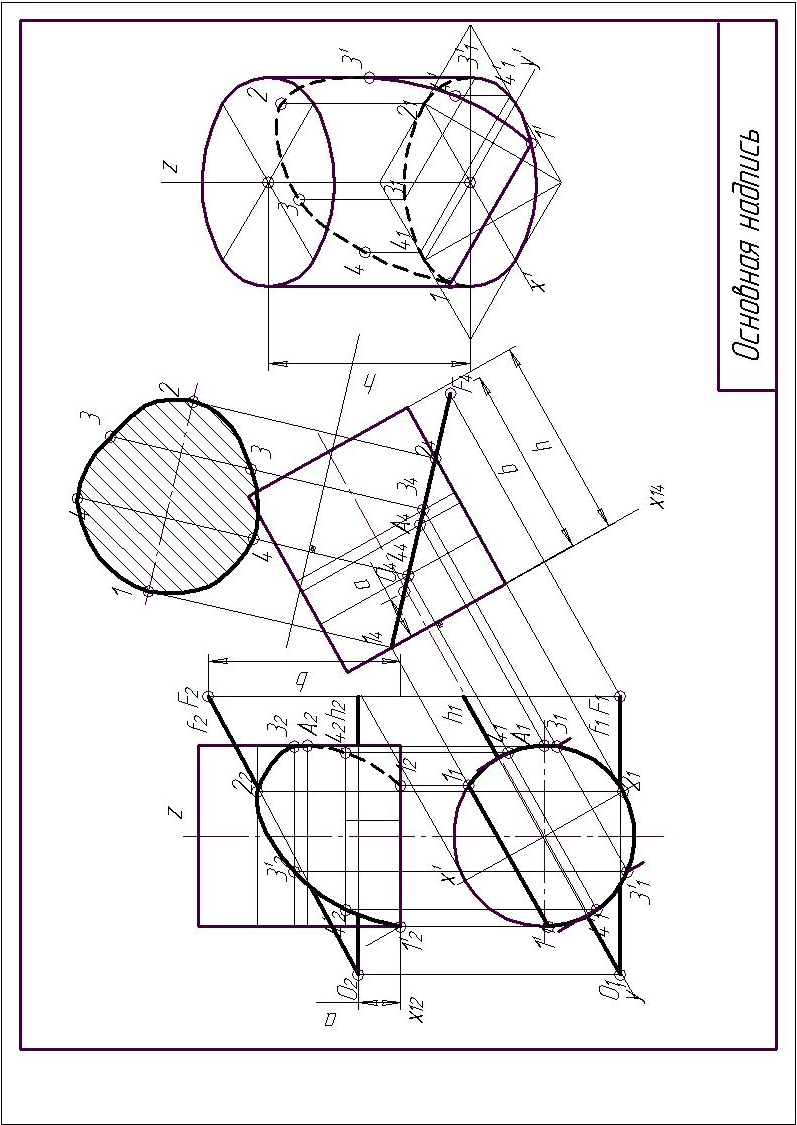
На рис. 25 и рис. 26 показан другой образец выполнения эпюра №3 «Пересечение сферы плоскостью общего положения», а на рис. 27 показан третий пример – «Пересечение цилиндра плоскостью общего положения». И в том, и в другом случае ход построения сечения такой же, как и описанный выше, но имеет свои особенности, так как плоскость сечения представлена не проецирующей, а общего положения.