
- •Введение
- •Тема 1 Жидкости и газы, их свойства
- •Определение жидкости
- •Основные свойства жидкостей и газов
- •Силы, действующие в жидкости
- •Тема 2 Гидростатика
- •2.1 Гидростатическое давление и его свойства
- •2.2. Основное уравнение гидростатики
- •2.3 Закон Паскаля и его техническое применение
- •2.4 Дифференциальные уравнения Эйлера равновесия жидкости
- •2.5 Абсолютное и избыточное давление. Вакуум
- •2.6 Приборы для измерения давления в жидкости
- •2.7 Сообщающиеся сосуды
- •2.8 Сила давления жидкости на плоские стенки
- •2.9 Закон Архимеда и его приложение
- •2.10. Поверхности равного давления
- •2.11 Сила давления жидкости на криволинейную стенку
2.11 Сила давления жидкости на криволинейную стенку
Возьмем криволинейную поверхность АВ с образующей, перпендикулярной к плоскости чертежа (рисунок 23), и определим силу давления жидкости на эту поверхность.
В ыделим
объем жидкости, ограниченный рассматриваемой
поверхностью АВ,
вертикальными
поверхностями, проведенными
через границы этого участка, и свободной
поверхностью жидкости,
т. е. объем АА/В/В,
и
рассмотрим условия его равновесия в
вертикальном и горизонтальном
направлениях. Если жидкость действует
на стенку АВ
с
силой F,
то
стенка АВ
действует
на жидкость с силой F,
направленной
в обратную сторону. На рисунке 23 показана
эта сила реакции, разложенная на две
составляющие: горизонтальную
FГ
и
вертикальную FB.
ыделим
объем жидкости, ограниченный рассматриваемой
поверхностью АВ,
вертикальными
поверхностями, проведенными
через границы этого участка, и свободной
поверхностью жидкости,
т. е. объем АА/В/В,
и
рассмотрим условия его равновесия в
вертикальном и горизонтальном
направлениях. Если жидкость действует
на стенку АВ
с
силой F,
то
стенка АВ
действует
на жидкость с силой F,
направленной
в обратную сторону. На рисунке 23 показана
эта сила реакции, разложенная на две
составляющие: горизонтальную
FГ
и
вертикальную FB.
Условие равновесия объема АА/В/В в вертикальном направлении имеет вид
![]() (30)
(30)
где р0 — давление на свободной поверхности жидкости;
SГ — площадь горизонтальной проекции поверхности АВ,
G=gV — вес тела давления (вес выделенного объёма жидкости).
Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности А/К и В/В взаимно уравновешиваются и остается лишь сила давления на площадь АК, т. е. на вертикальную проекцию поверхности А В — SB. Тогда
![]() (31)
(31)
Определив по формулам (31) и (32) вертикальную и горизонтальную составляющие полной силы давления F, найдем
![]() (32)
(32)
И направлена под углом к горизонту
![]() (33)
(33)
Тело давления — это объём, ограниченный криволинейной стенкой АВ, вертикалями, проведёнными через её контуры АА/ и ВВ/ и свободной поверхностью жидкости А/В/ или её продолжением. Тело давления считается реальным, если оно заполнено жидкостью (Рв при этом направлена вниз), и фиктивным — если жидкостью не заполнено (Рв при этом направлена вверх).
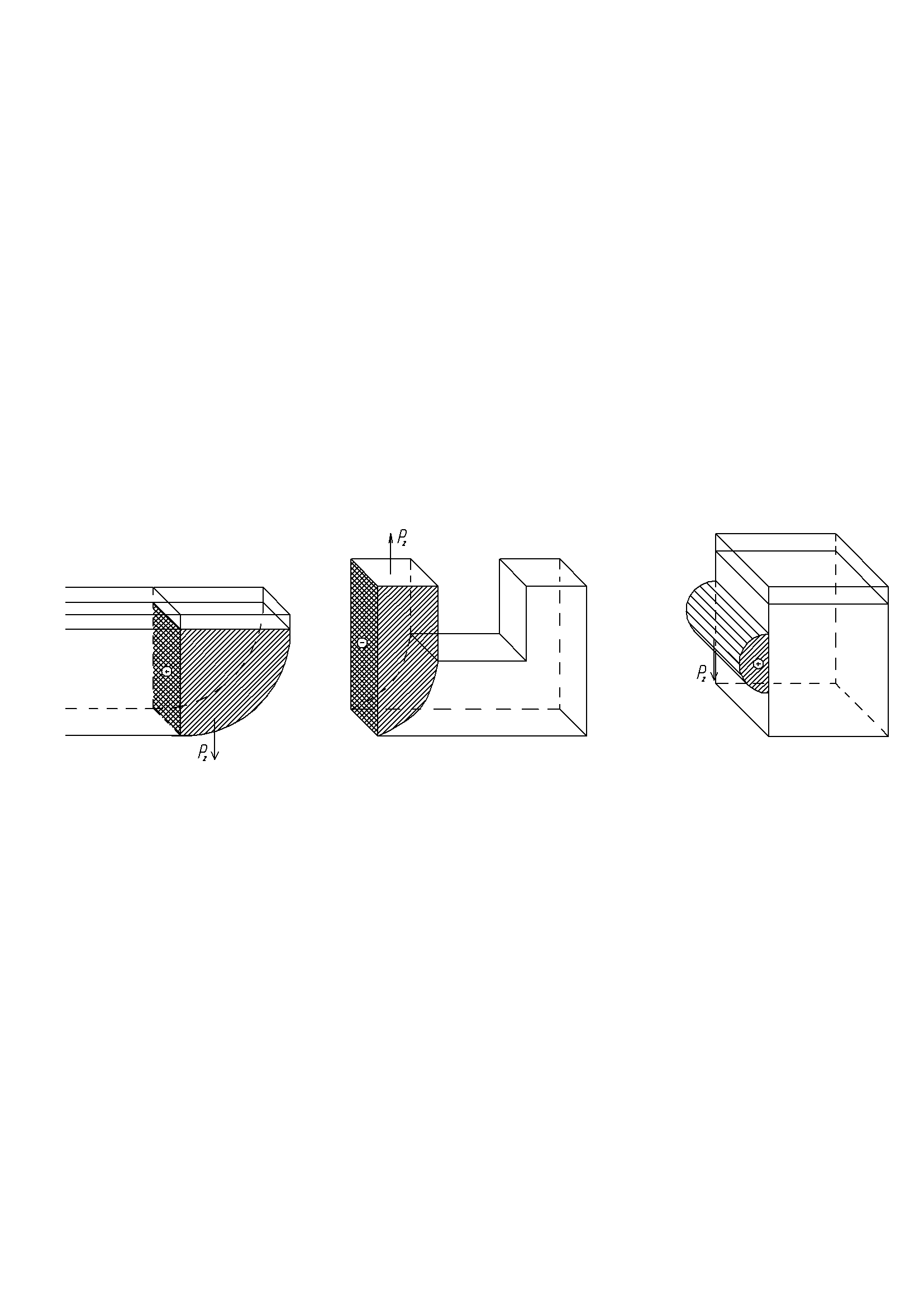
Рис. 24 тела давления а, в – реальные; б - фиктивное
Задача:
Определим
силу давления нефти Р на цилиндрическую
стенку резервуара и угол наклона
линии действия этой силы к горизонту
,
если радиус R=0,8
м; ширина стенки В=3 м, высота нефти в
резервуаре Н=2 м. Относительная плотность
нефти н=0,9.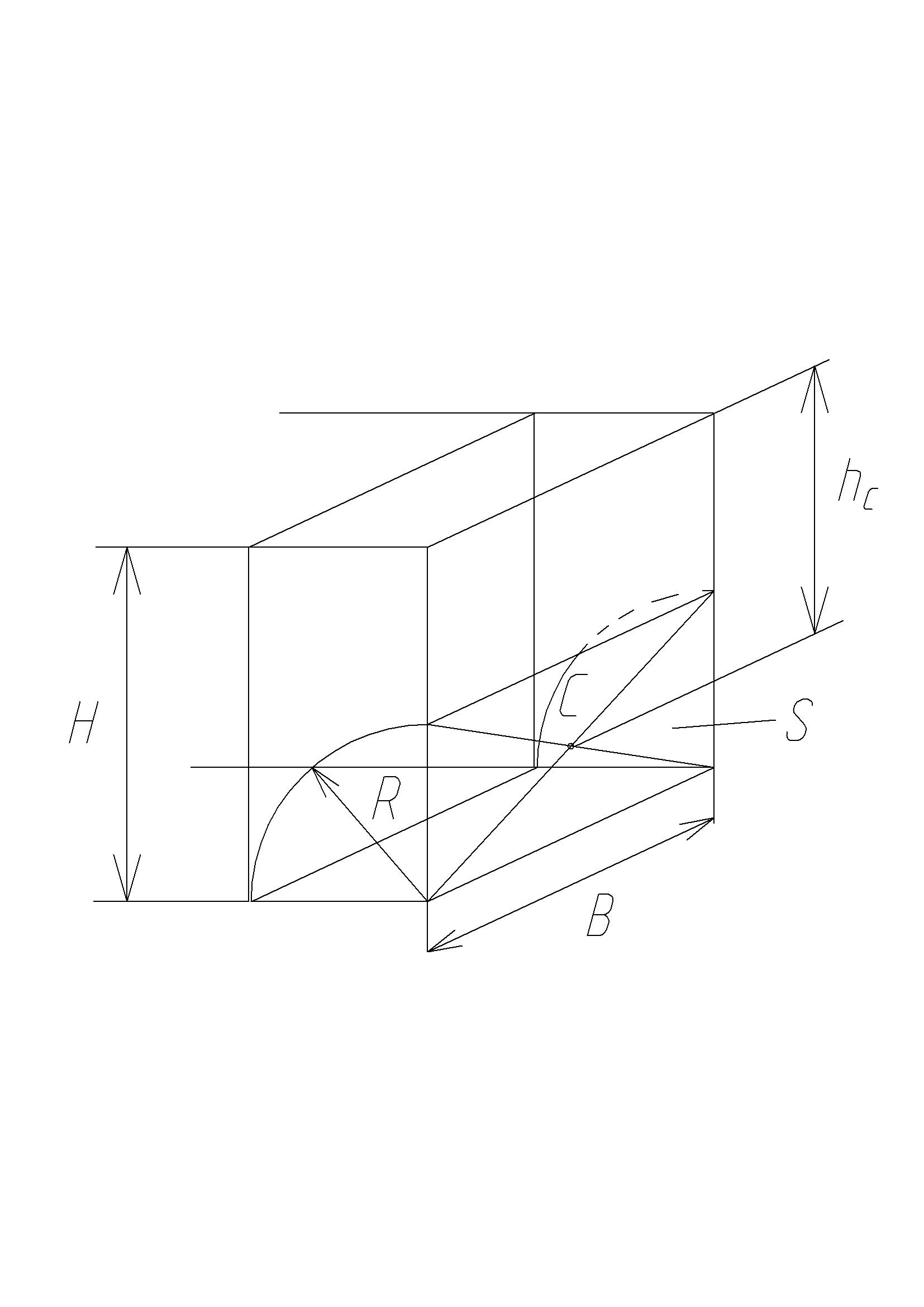
Решение:
Вертикальная
проекция криволинейной стенки представляет
собой прямоугольник, площадь которого
равна
![]()
Расстояние центра тяжести S от свободной поверхности нефти равно
![]()
Тело давления представляет собой разность объемов параллелепипеда высотой Н, шириной В, и длиной R и четверти цилиндра с радиусом R и шириной В.
![]()
Таким
образом, по уравнениям
![]() ,
,
![]() ,
,
![]()
![]()
![]()
Угол наклона линии действия силы давления к горизонту определим из уравнения
![]()
