
- •Введение
- •Методические вопросы лабораторного практикума
- •Методические вопросы контрольной работы
- •Содержание и объем контрольной работы
- •Теоретические вопросы контрольной работы
- •Алгоритм выбора задания контрольной работы
- •Содержание описательной части контрольной работы:
- •Оформление контрольной работы
- •Защита контрольной работы и сдача зачета
- •Методические указания к решению задач
- •Работа 1. Интерполяция и аппроксимация таблично заданных функций
- •Содержание и порядок выполнения работы
- •Краткие сведения из теории
- •Определение коэффициентов аппроксимирующей функции с помощью надстройки «Поиск решения»
- •Технология подбора аппроксимирующей функции в среде эт путем построения линий тренда
- •Работа 2. Методы решения систем линейных алгебраических уравнений
- •Содержание и порядок выполнения работы
- •Краткие сведения из теории и компьютерной технологии
- •Метод Гаусса решения слау
- •Матричный метод решения слау
- •Технология работы с матричными функциями
- •Методика решения слау с помощью надстройки «Поиск решения»
- •Решение слау методом простой итерации
- •Вычисляем первое приближение по формулам (12), подставляя в них начальное приближение (13).
- •Решение слау методом Зейделя
- •Итерационный процесс поиска решения системы завершается, если выполняются условия (10).
- •Решение обыкновенного дифференциального уравнения первого порядка методом Эйлера
- •Модифицированный метод Эйлера
- •Методы Рунге-Кутта
- •Решение обыкновенных дифференциальных уравнений в среде электронных таблиц
- •Продолжение таблицы 9
- •Краткие сведения из теории
- •Задача оптимизации производственного плана предприятия
- •Математическая модель задачи
- •Математическая модель
- •Графический метод решения задачи лп
- •Решение задачи лп в среде электронных таблиц
- •Технология работы с надстройкой «Поиск решения»
- •Работа 5. Транспортная задача Цель работы. Освоить методику составления математической модели транспортной задачи и методы ее решения. Содержание и последовательность выполнения работы
- •Краткие сведения из теории
- •Математическая модель транспортной задачи
- •Виды моделей транспортной задачи
- •Математическая модель задачи
- •Методы решения транспортной задачи
- •Метод потенциалов
- •Алгоритм метода потенциалов
- •Решение транспортной задачи в среде эт
- •Задания Работа 1. Интерполяция и аппроксимация таблично заданных функций
- •Работа 2. Методы решения систем линейных алгебраических уравнений
- •Работа 3. Численные методы решения обыкновенных дифференциальных уравнений
- •Работа 4. Задача оптимизации производственной программы выпуска продукции
- •Работа 5. Транспортная задача
- •Список рекомендуемой литературы
Метод потенциалов
В теории линейного программирования доказывается, что любая транспортная задача имеет оптимальный план. Возникает вопрос: как проверить план на оптимальность и будет ли единственным оптимальный план?
Существует простая методика проверки
планов на оптимальность. В основу ее
положен метод потенциалов. Смысл его
заключается в следующем. Каждому заводу
поставщику присваивают некоторую
величину
![]() которую называют потенциалом завода,
а каждому строительному объекту –
величину
которую называют потенциалом завода,
а каждому строительному объекту –
величину
![]() -
потенциал строительного объекта. Эти
величины связаны между собой соотношениями:
-
потенциал строительного объекта. Эти
величины связаны между собой соотношениями:
для переменных
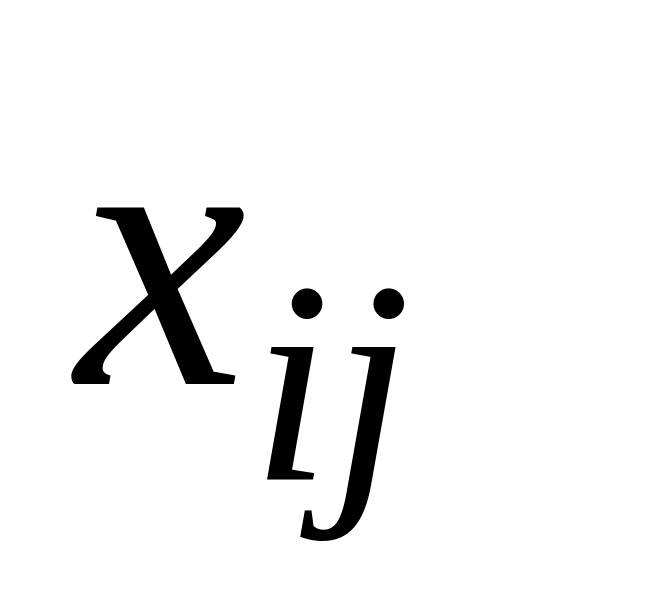 заполненных клеток (базисных переменных)
заполненных клеток (базисных переменных)
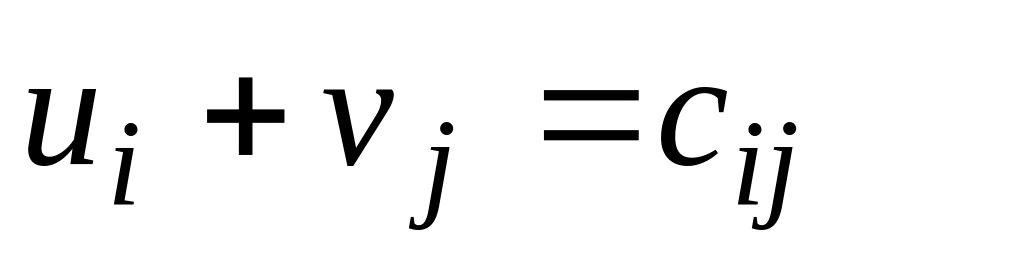 (5)
(5)для переменных
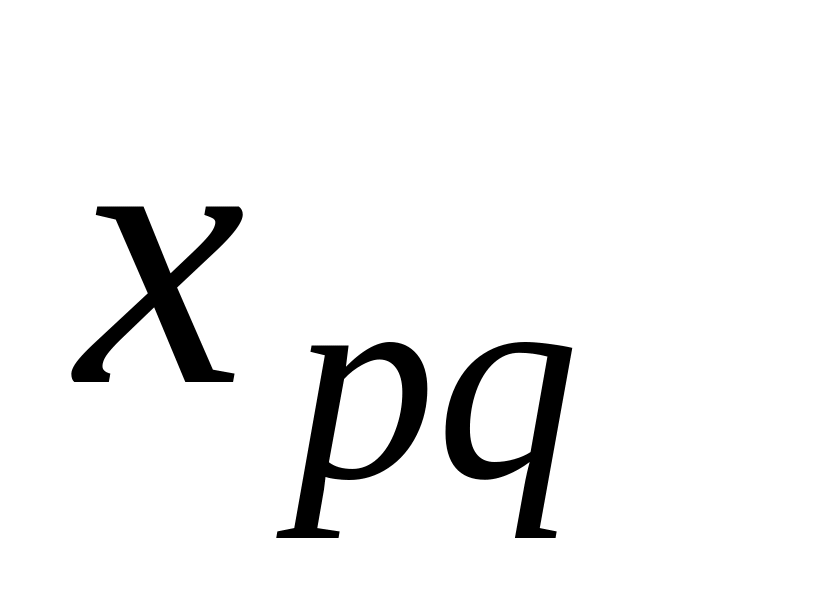 незаполненных клеток (свободных
переменных)
незаполненных клеток (свободных
переменных)
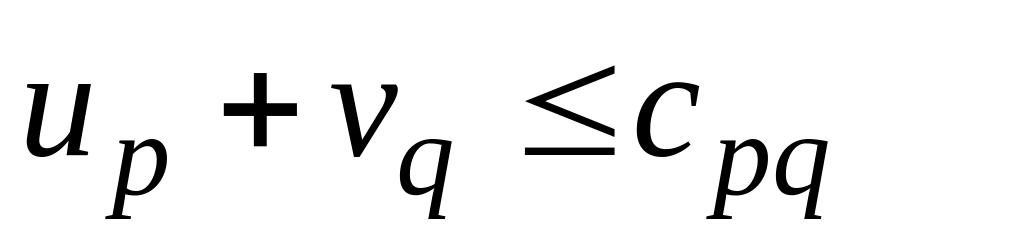 (6)
(6)
Здесь
![]() -
стоимость доставки единицы продукции
от
-го завода к
- му строительному объекту заполненных
клеток,
-
стоимость доставки единицы продукции
от
-го завода к
- му строительному объекту заполненных
клеток,
![]() -
стоимость доставки для незаполненных
клеток.
-
стоимость доставки для незаполненных
клеток.
Алгоритм метода потенциалов
Устанавливают вид модели транспортной задачи (открытая или закрытая). При необходимости делают модель закрытой.
Определяют первый опорный план с учетом стоимости доставки продукции.
Проверяют опорный план на вырожденность. При необходимости вводят нулевые поставки.
Проверяют опорный план на оптимальность. Для чего определяют потенциалы поставщиков и потребителей по выражениям (5) для базисных переменных и анализируются неравенства (6) для свободных переменных:
если хотя бы одно из неравенств не выполняется, то план неоптимальный и для его улучшения изменяют значение свободной переменной невыполняемого неравенства;
если все неравенства выполняются и среди неравенств имеются равенства, то план оптимальный и не единственный.
Проверим алгоритм метода на примере 1. Исходная модель транспортной задачи является закрытой. В качестве первого опорного плана возьмем вариант 2 (таблица 5).
Вариант 2. Базисные переменные (заполненные клетки):
![]()
Количество заполненных клеток на единицу меньше суммы количества поставщиков и потребителей, т.е. опорный план невырожденный. Для нахождения значений потенциалов составляем систему равенств:
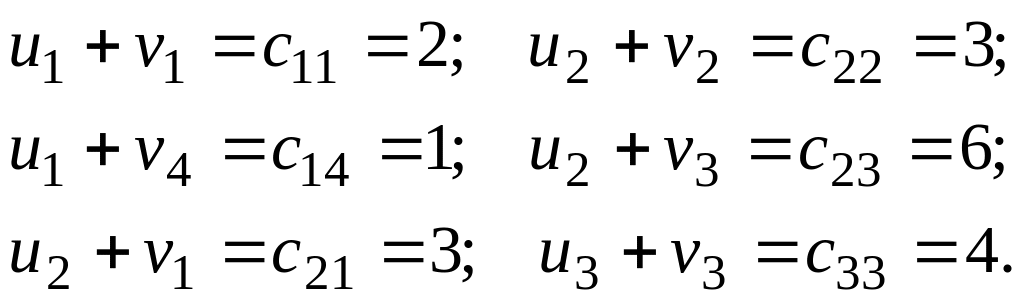
Так как равенств 6, а неизвестных 7, то
система является неопределенной. Поэтому
для определенности системы считаем
значение одного из потенциалов известным,
например,
![]() ,
тогда:
,
тогда:
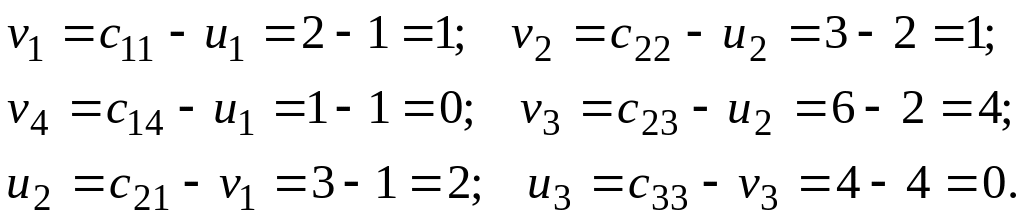
Составляем неравенства для незаполненных клеток и анализируем их
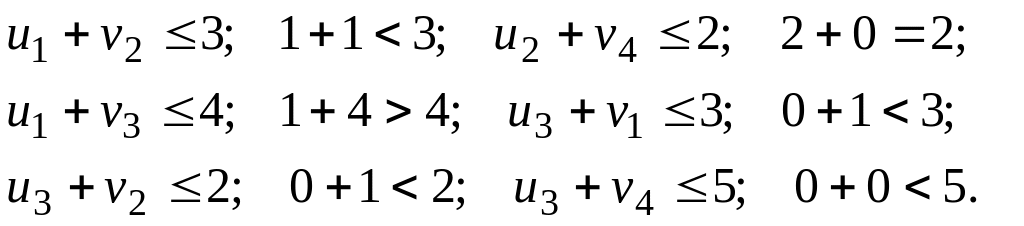
Одно
из неравенств не выполняется, следовательно,
план неоптимальный. Это неравенство
соответствует переменной
![]() т.е.
для улучшения плана необходимо эту
переменную ввести в басис, присвоив ей
некоторую величину
т.е.
для улучшения плана необходимо эту
переменную ввести в басис, присвоив ей
некоторую величину
![]() Переход к новому базису осуществляется
с помощью построения цикла и
перераспределения перевозимой продукции.
Строим цикл с вершинами в занятых клетках
(1,1), (2,1), (2,3) и незанятой клетки (1,3), в
которой не выполняются условия
оптимальности. Для определения величины
Переход к новому базису осуществляется
с помощью построения цикла и
перераспределения перевозимой продукции.
Строим цикл с вершинами в занятых клетках
(1,1), (2,1), (2,3) и незанятой клетки (1,3), в
которой не выполняются условия
оптимальности. Для определения величины
![]() в незанятую клетку (1,3) поставим знак
«+», а другие вершины цикла отметим
чередованием знаков «-» и «+» (см. таблицу
5). Затем определяем
в незанятую клетку (1,3) поставим знак
«+», а другие вершины цикла отметим
чередованием знаков «-» и «+» (см. таблицу
5). Затем определяем
![]() где
где
![]() -
количество продукции в клетках вершин
цикла, отмеченных знаком «-»:
-
количество продукции в клетках вершин
цикла, отмеченных знаком «-»:
![]()
Так как суммы значений неизвестных по строкам и столбцам должны оставаться неизменными, то следует произвести балансовый перерасчет (см. таблицу 5). В итоге перерасчета приходим к варианту 1 (см. таблицу 4).
Выполним анализ варианта 3 (таблица 6).
Вариант 3. Базисные переменные:
![]()
Опорный план невырожденный. Составляем систему равенств, определяемых базисными переменными:
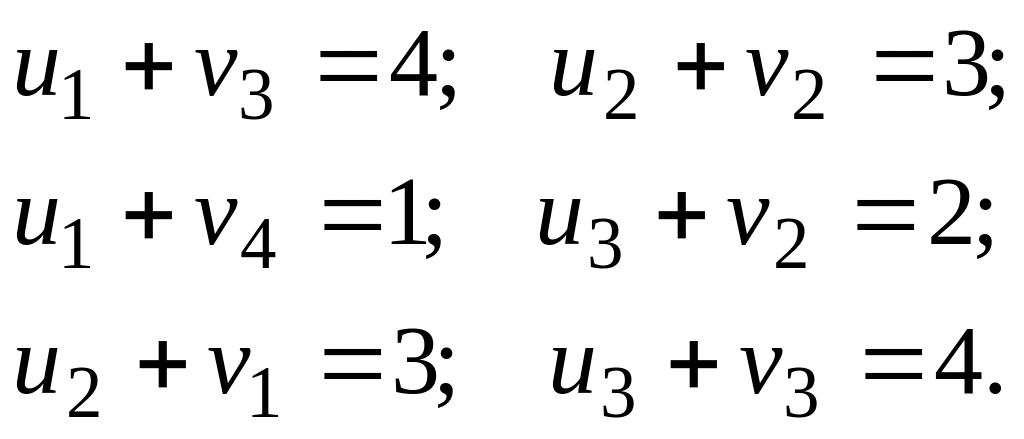
Так как равенств 6, а неизвестных 7, то полагаем , тогда:
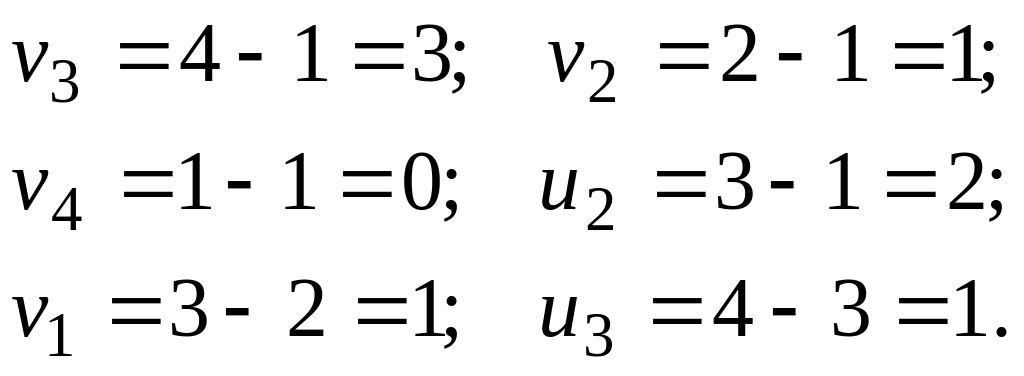
Составляем неравенства для незаполненных клеток
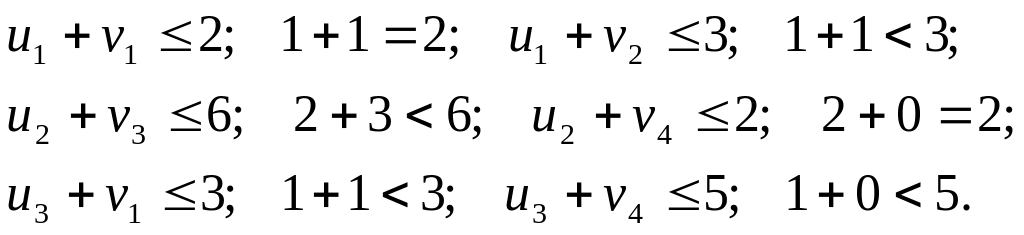
Все
неравенства выполняются и среди
неравенств имеются равенства,
следовательно, план оптимальный и не
единственный. Равенства соответствуют
переменным
![]() Изменяя
значения этих переменных, можно получить
новые оптимальные планы. Один из них
приведен в таблице 4.
Изменяя
значения этих переменных, можно получить
новые оптимальные планы. Один из них
приведен в таблице 4.
