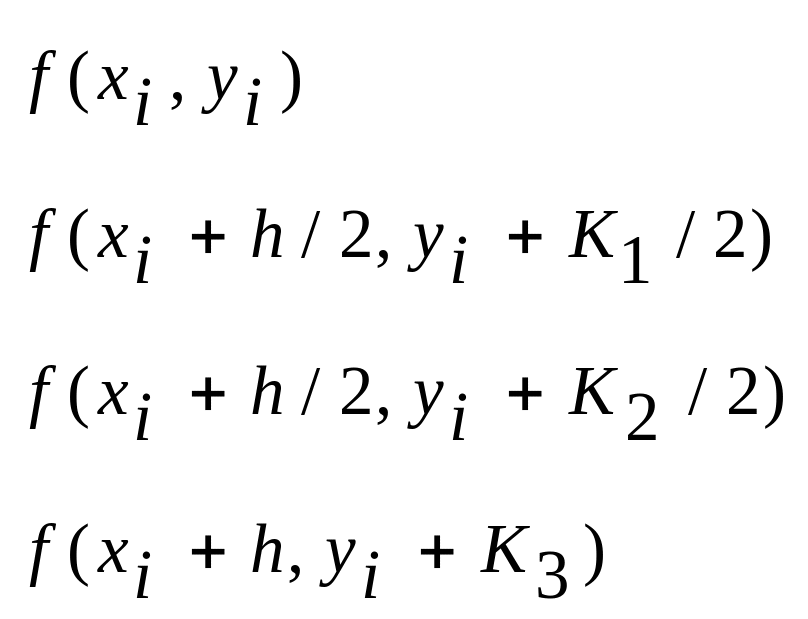Методы Рунге-Кутта

Для получения более высокой точности необходимо добиться лучшей аппроксимации производной. Эта идея заложена в основу методов Рунге-Кутта, отличающихся друг от друга схемами расчета координат внутренних точек, в которых вычисляются значения производных. Так как существуют различные способы выбора расположения внутренних точек и относительных весов для найденных производных, методы Рунге-Кутта, по существу, объединяют целое семейство методов решения дифференциальных уравнений. Наиболее распространен метод, в котором удерживаются составляющие разложения решения в ряд Тейлора (2), включая содержащую Это метод четвертого порядка точности, для него погрешность вычислений на каждом шаге интегрирования имеет порядок Расчеты выполняются по формуле

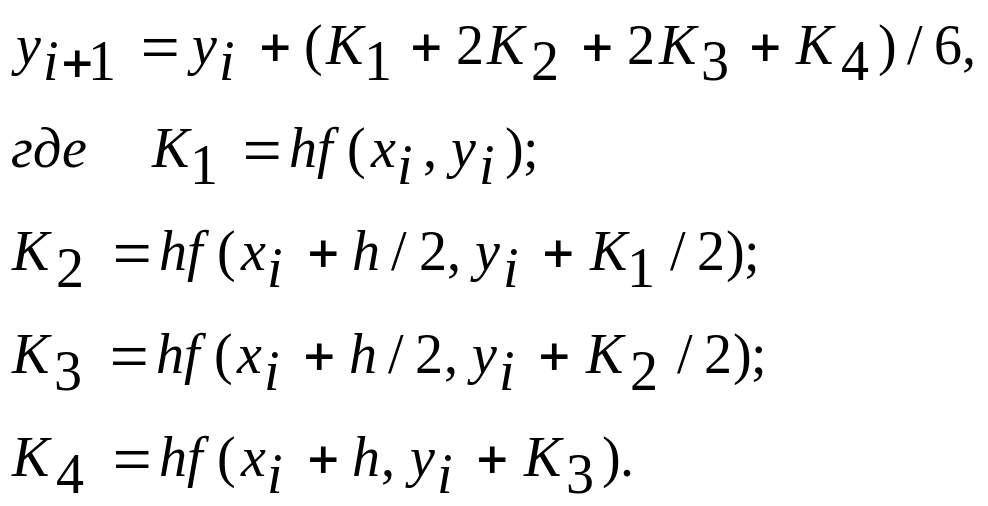(8)

По сравнению с методом Эйлера метод Рунге-Кутта имеет важное преимущество, так как обеспечивает более высокую точность, что позволяет увеличить шаг интегрирования и, следовательно, уменьшить количество вычислений. Все вычисления удобно выполнять в таблице 3.

Таблица 3.Табличный алгоритм метода Рунге-Кутта IV порядка точности

Пример 3. Методом Рунге-Кутта IV порядка точностинайти решение уравнения при начальном условии на отрезке [0; 0,2], приняв шаг интегрирования = 0,2.

Точное решение уравнения .

Решение. Результаты расчета представим в таблице 4.

Таблица 4. Итоговая таблица расчетов методом Рунге-Кутта

	х
0	0 0,1 0,1 0,2	1 1,1 1,09182 1,181728	1 0,9182 0,90864 0,843238	0,2 0,18364 0,181728 0,168647	0,2 0,36728 0,363456 0,168647	1
1	0,2	1,18323	…			1,18322

Пояснения к таблице 4

При =0:

• Записываем в первой строке

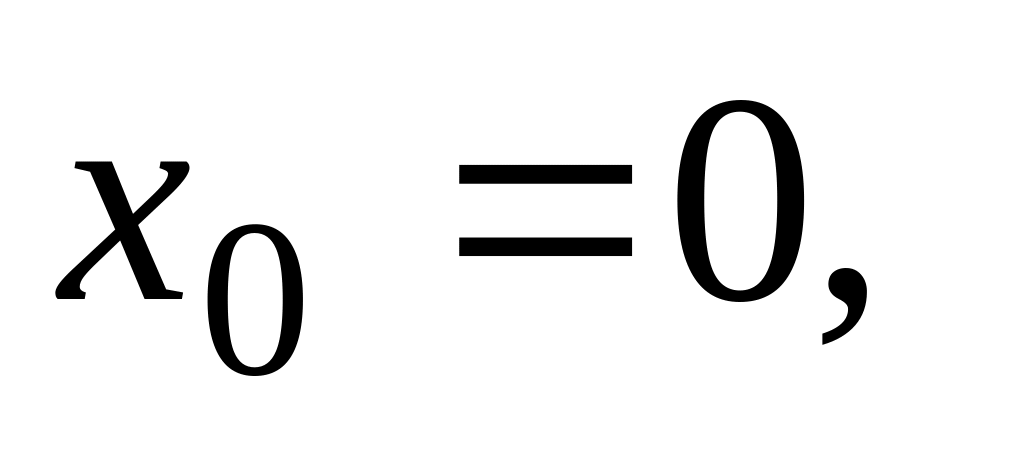
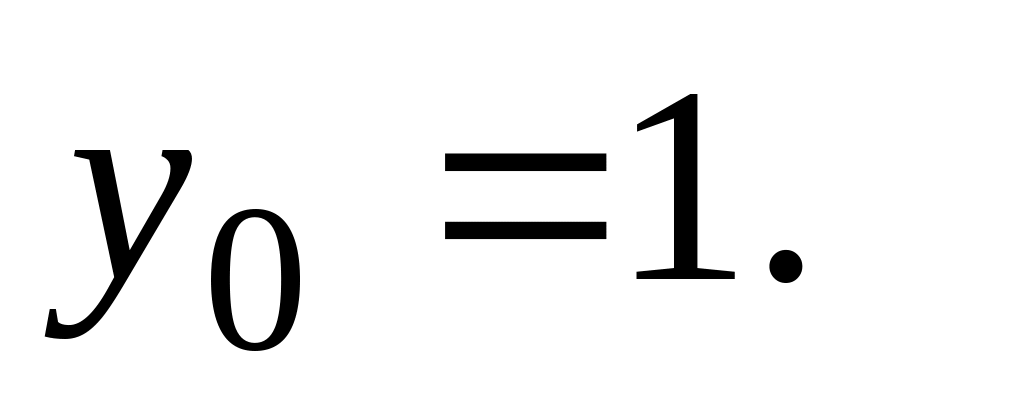
• Вычисляем 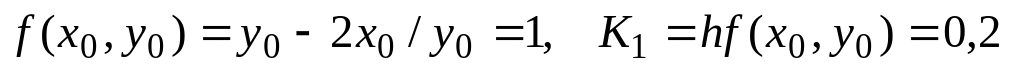и заносим полученные значения в первую строку.

• Записываем во второй строке

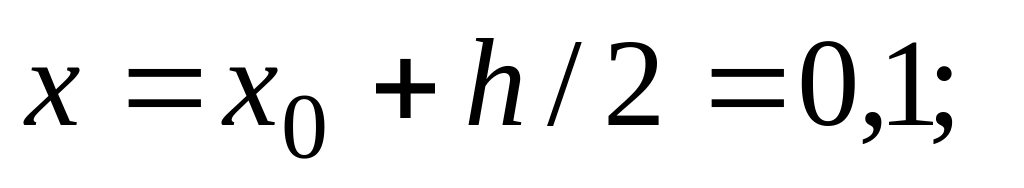
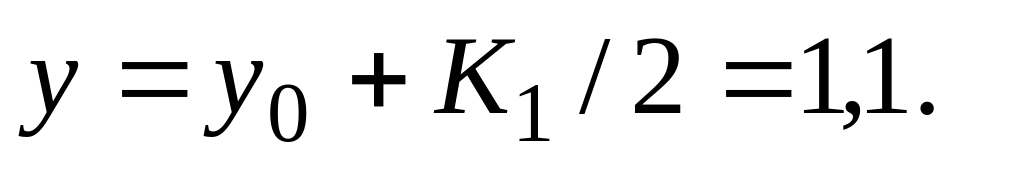
• Вычисляем

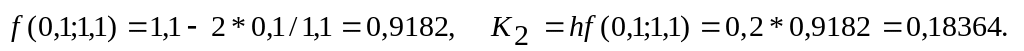
• В третью строку записываем

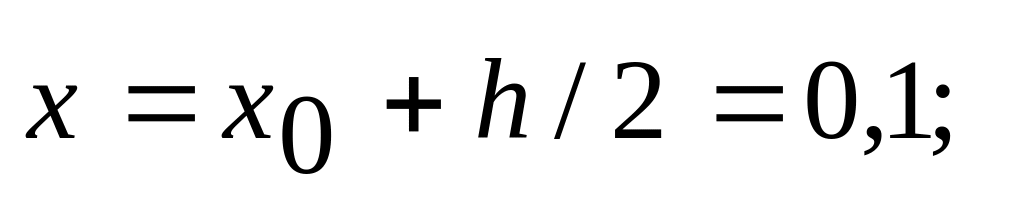
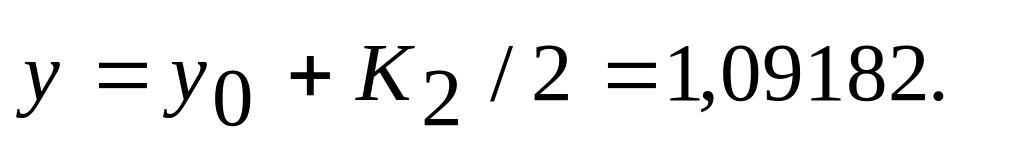
• Определяем

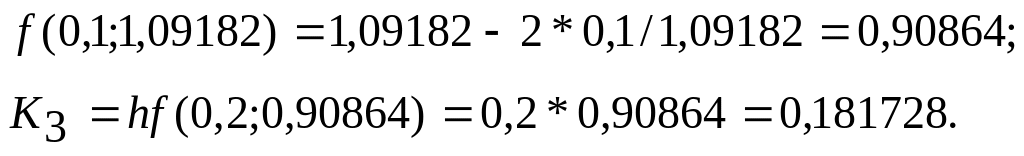
• Записываем в четвертой строке таблицы

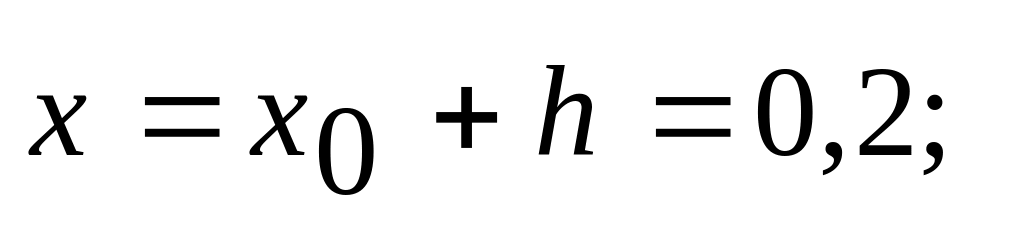
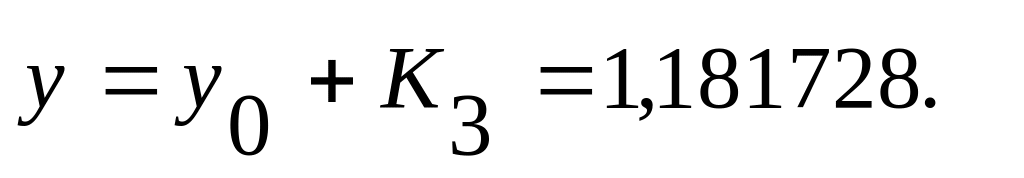
• определяем

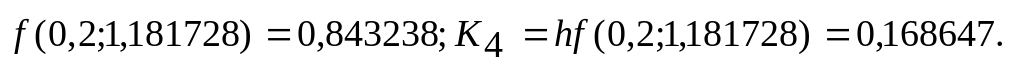
• В столбце записываем числа .

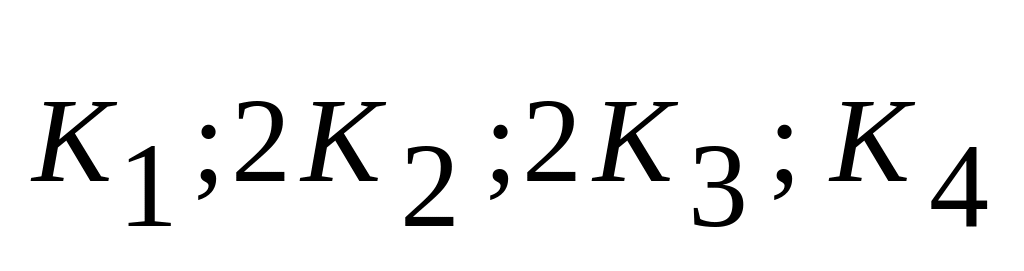• Определяем

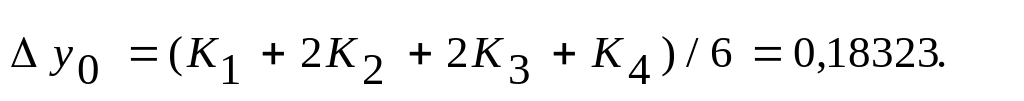
• Получаем

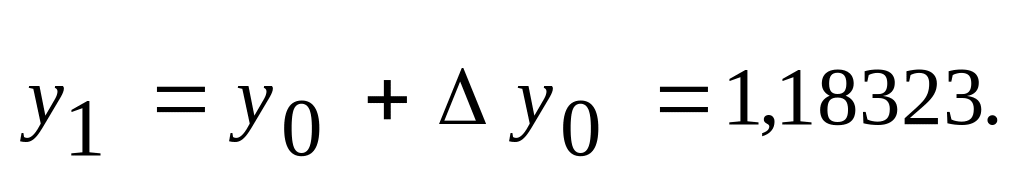
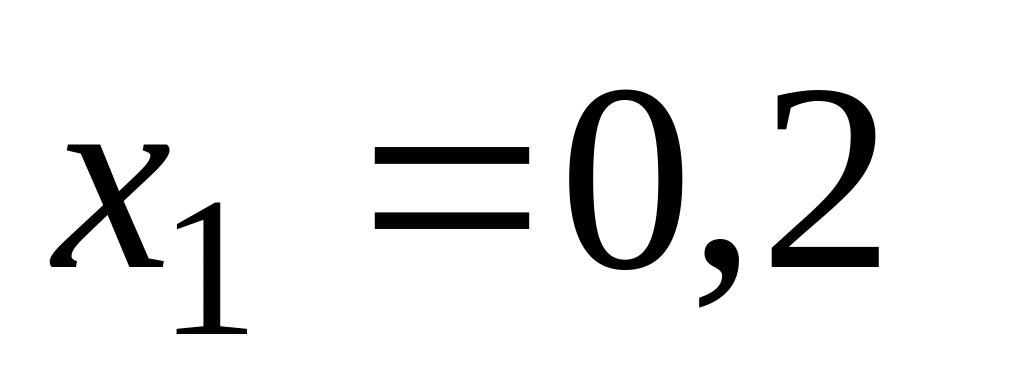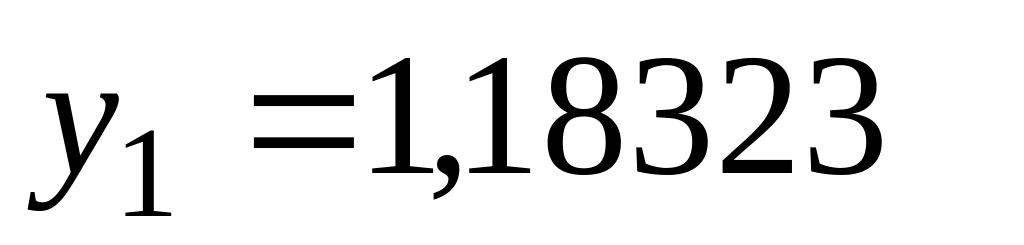• Значения и заносим в строку, отмеченную индексом =1, и проводим аналогичные вычисления.

Сравнивая с точным решением, находим, что абсолютная погрешность составляет  = 0,00001. Заметим, что это достигнуто при интегрировании с шагом = 0,2. Следовательно, точность метода Рунге-Кутта IV порядка точности намного превышает точность методов Эйлера. Собственно, методы Эйлера могут рассматриваться как частные случаи метода Рунге-Кутта с первым и вторым порядком точности.

К важным преимуществам схем Рунге-Кутта, кроме хорошей точности, следует отнести возможность расчетов с переменным шагом, что особенно важно при расчетах на ЭВМ и реализовано во всех алгоритмах и стандартных программах метода.

В алгоритмах решения дифференциальных уравнений с автоматическим выбором шага интегрирования оценка погрешности определяется по правилу Рунге: при переходе от к расчет производится дважды (с шагом и шагом ). Если при расчете точность  окажется больше заданной погрешности , то шаг уменьшается вдвое и процедура повторяется. Если  значительно меньше , то шаг увеличивается вдвое при переходе к точке . Шаг интегрирования не изменяется, если  незначительно меньше .

где - порядок точности метода.

Как получить требуемую точность расчетов, если неизвестно точное решение дифференциального уравнения?

На практике обычно используют правило Рунге. Если есть численные решения на двух сетках с шагом т.е. то погрешность вычислений в точке равна:

где - порядок точности метода; - точное решение в точке .

Для оценки погрешности расчетов любым методом поступают следующим образом:

• разбивают отрезок интегрирования 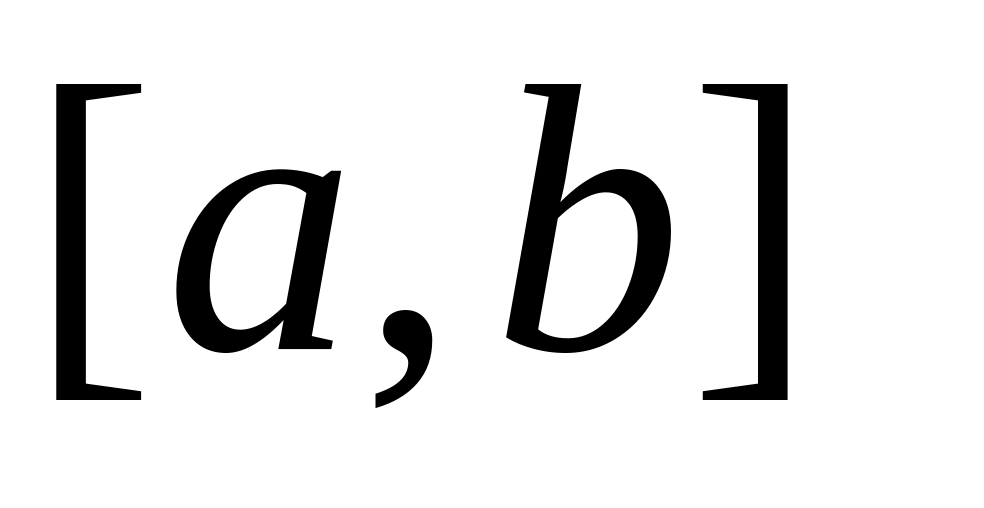на частей;

• вычисляют приближенное решение дифференциального уравнения на сетке 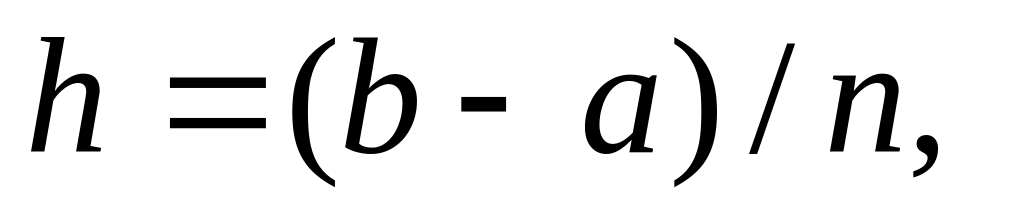которое обозначают

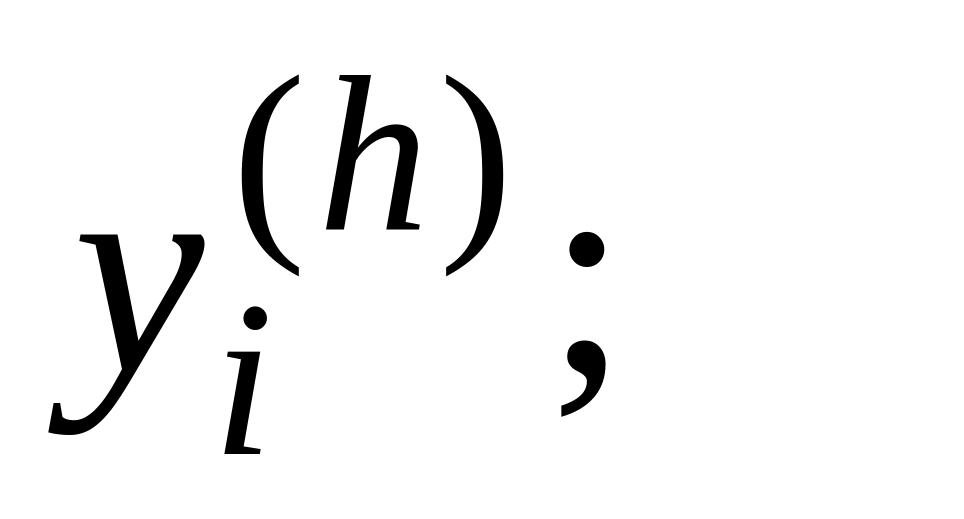
• затем вычисляют приближенное решение этого уравнения на сетке 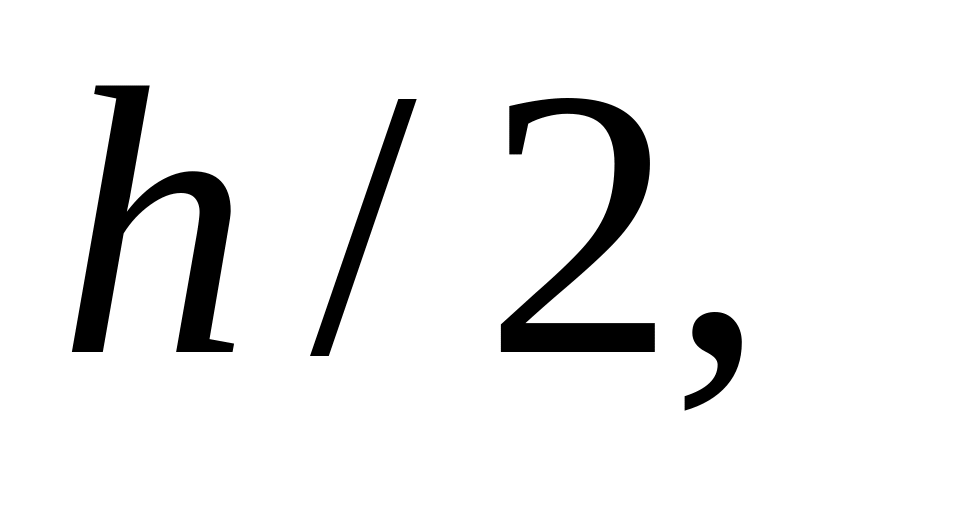которое обозначают

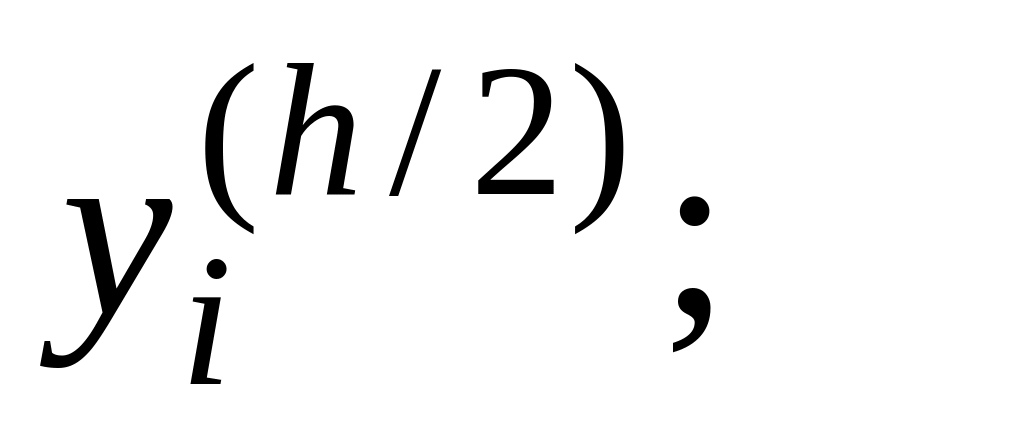
• окончательным приближенным решением дифференциального уравнения считают значения 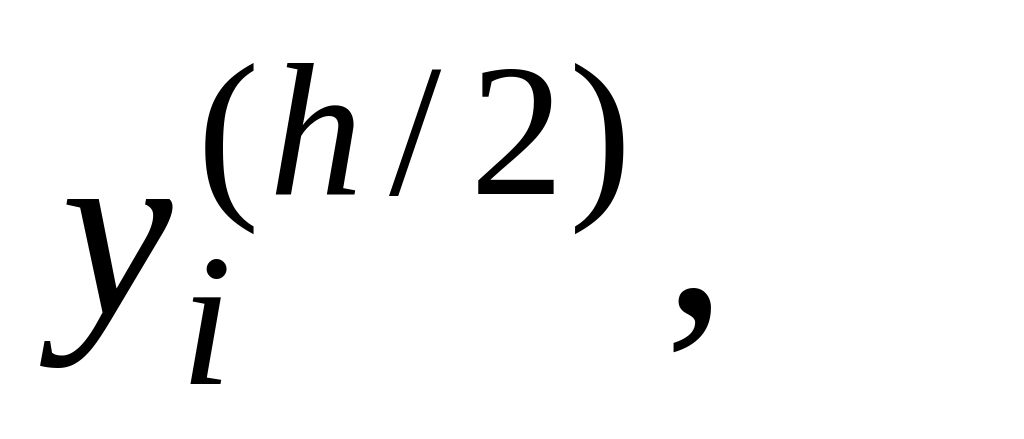при этом погрешность решения в точке равна:

• для метода Эйлера (порядок точности )

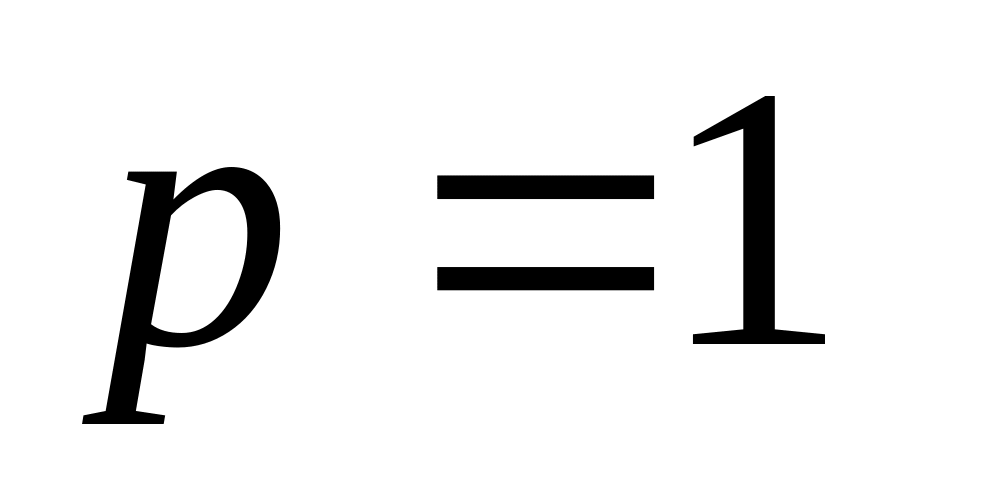• для модифицированного метода Эйлера (порядок точности )

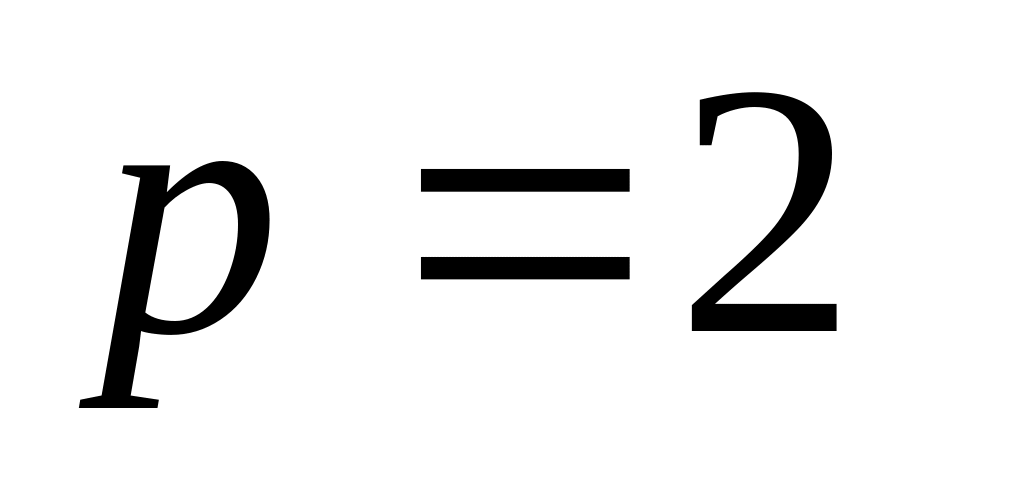• для метода Рунге-Кутта (порядок точности )
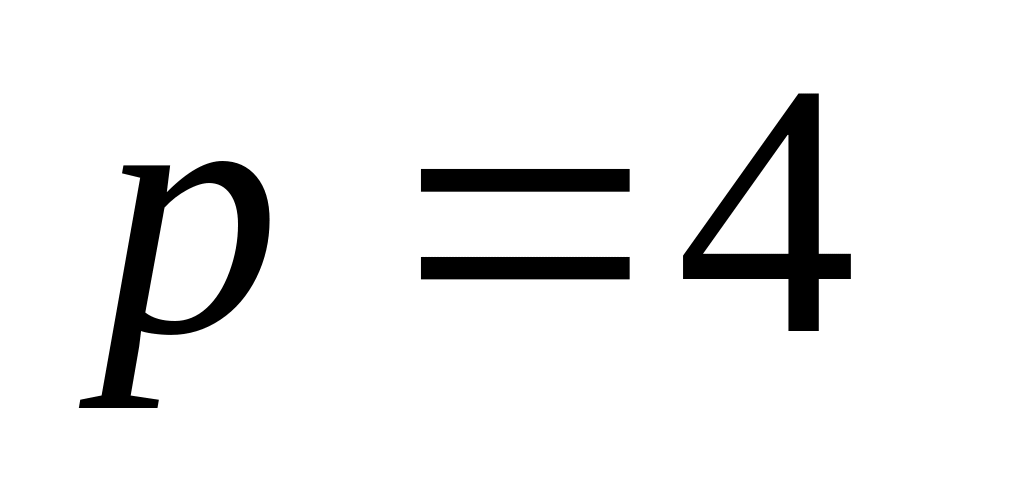