
- •Тема 3 Предел функции в точке
- •Неопределённость вида .
- •4. Найти предел функции (неопределённость ):
- •5. Найти предел функции:
- •Домашнее задание 3
- •1. Используя ( - ) определение предела функции в точке,
- •2. Найти предел функции:
- •Тема 4 Непрерывные функции. Точки разрыва функции. Задачи для практического занятия
- •Домашнее задание 4
- •Тема 5 Производная и дифференциал
- •Домашнее задание 5
- •Тема 6 Применение производной
- •Домашнее задание 6
- •Тема 7 Исследование функций и построение графиков
- •Домашнее задание 7
Тема 6 Применение производной
1. Написать уравнение касательной и нормали к данной кривой в
точке с абсциссой xо= 1 :
а)
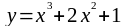 ; б)
; б)
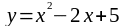 ;
;
в) .
2. В какой точке касательная к кривой
а )
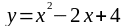 образует с осью Ох угол 45?
образует с осью Ох угол 45?
б)
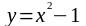 параллельна прямой
параллельна прямой
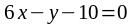 ?
?
в)
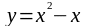 перпендикулярна прямой
перпендикулярна прямой
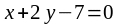 ?
?
3. Вычислить приближенно:
а) arctg
0,981; б)
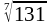 ;
в) sin
32.
;
в) sin
32.
4. Найти пределы, используя правило Лопиталя:
а)
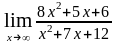 ;
б)
;
б)
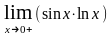 ;
;
в)
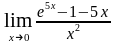 ;
г)
;
г)
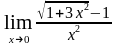 .
.
5.
Доопределить функцию
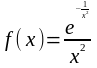 в точке разрыва так,
в точке разрыва так,
чтобы она стала непрерывной.
6.
Проверить, является ли функция
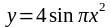
эластичной в
точке xо=
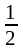 .
.
Домашнее задание 6
1. Написать уравнение касательной и нормали к кривой:
а)
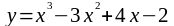 в точке с абсциссой xо=
1;
в точке с абсциссой xо=
1;
б) заданной
неявно
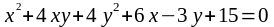 в
в
точке Mо(2; 1) ;
в) заданной
параметрически
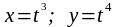 в точке
tо=
1.
в точке
tо=
1.
2. В какой точке касательная к кривой
а )
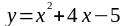 образует с прямой
образует с прямой
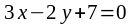 угол 45?
угол 45?
б)
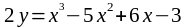 параллельна прямой
параллельна прямой
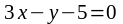 ?
?
в)
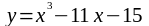 перпендикулярна прямой
перпендикулярна прямой
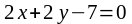 ?
?
3. Вычислить приближенно:
а) arcsin
0,591.; б)
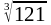 ;
в) sin
29.
;
в) sin
29.
4. Найти пределы, используя правило Лопиталя:
а)
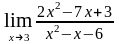 ;
б)
;
б)
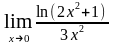 ;
;
в)
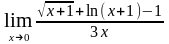 ;
г)
;
г)
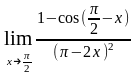 .
.
5.
Доопределить функцию
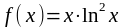 в точке разрыва
в точке разрыва
так, чтобы она стала непрерывной.
6.
Проверить, является ли функция
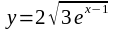
эластичной в точке xо= 1.
7. Найти угол, под которым пересекаются линии
 ,
,
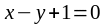 .
.
Тема 7 Исследование функций и построение графиков
Общая схема исследования функции и построения графика
Определение общего характера графика функции:
-нахождение области определения функции;
-исследование функции на чётность, нечётность,
периодичность;
-исследование функции на непрерывность функции и
точки разрыва,
-нахождение вертикальных, горизонтальных
и наклонных асимптот графика функции;
-нахождение точек пересечения графика функции с
осями координат;
-нахождение интервалов знакопостоянства функции;
-нахождение дополнительных точек графика
функции.
Уточнение характера графика функции с помощью первой производной:
-нахождение интервалов монотонности функции;
-нахождение точек экстремумов функции.
Уточнение характера графика функции с помощью второй производной:
-нахождение интервалов выпуклости вверх,
выпуклости вниз;
-нахождение точек перегиба функции.
1. Найти асимптоты графика функции:
а)
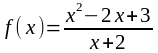 ;
б)
;
б)
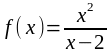 .
.
2. Найти промежутки монотонности функции:
а)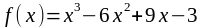 ; б)
; б)
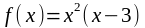 ;
в)
;
в)
 .
.
3. Найти экстремумы функции:
а)
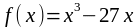 ;
б)
;
б)
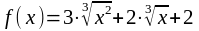 ;
в)
;
в)
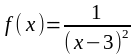 .
.
4. Исследовать методами дифференциального
исчисления следующие функции и построить графики:
а)
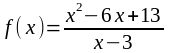 ;
б)
;
б)
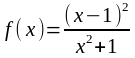 ;
;
в)
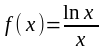 ;
г)
;
г)
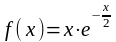 .
.
