
- •Тема 3 Предел функции в точке
- •Неопределённость вида .
- •4. Найти предел функции (неопределённость ):
- •5. Найти предел функции:
- •Домашнее задание 3
- •1. Используя ( - ) определение предела функции в точке,
- •2. Найти предел функции:
- •Тема 4 Непрерывные функции. Точки разрыва функции. Задачи для практического занятия
- •Домашнее задание 4
- •Тема 5 Производная и дифференциал
- •Домашнее задание 5
- •Тема 6 Применение производной
- •Домашнее задание 6
- •Тема 7 Исследование функций и построение графиков
- •Домашнее задание 7
Тема 3 Предел функции в точке
1. Используя ( - ) определение предела функции в точке,
доказать, что
а)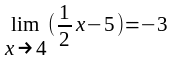 ; б)
; б)
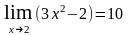 .
.
Указать ().
2. Найти предел функции :
а) ; б)
; б)
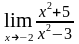 ;
в)
;
в)
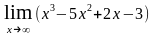 .
.
Неопределённость
вида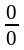 .
.
Чтобы раскрыть неопределённость вида , заданную отношением двух многочленов, необходимо выделить в числителе и знаменателе множитель, равный нулю при предельном значении х и сократить на этот множитель, а затем перейти к пределу.
3. Найти предел функции (неопределённость ):
а)
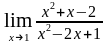 ; б)
; б)
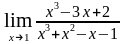 ;
;
в)
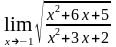 ;
г)
;
г)
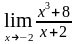 ;
;
д)
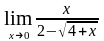 ; е)
; е)
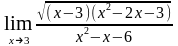 ;
;
ж)
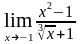 ;
з)
;
з)
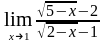 .
.
Неопределённость вида .
Чтобы раскрыть неопределённость вида , заданную отношением двух многочленов, необходимо разделить числитель и знаменатель почленно на х n, где n – степень многочлена в знаменателе.
4. Найти предел функции (неопределённость ):
а)
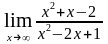 ; б)
; б)
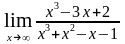 ;
;
в)
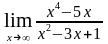 ;
г)
;
г)
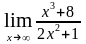 ;
;
д)
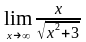 ; е)
; е)
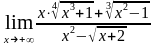 .
.
. Неопределённость вида –
С помощью различных преобразований (приведение к общему знаменателю, умножение на «сопряжённое» выражение) неопределённость вида ( – ) приводят к неопределённостям вида или .
5. Найти предел функции:
а)
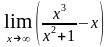 ; б)
; б)
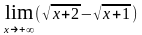 ;
;
в)
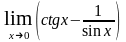 ;
г)
;
г)
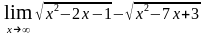 .
.
6. Найти предел функции, используя первый замечательный
предел или следствия:
а)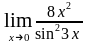 ;
б)
;
б) ;
;
в)
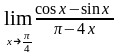 ;
г)
;
г)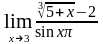 .
.
7. Найти предел функции, используя второй замечательный
предел или следствия:
а)
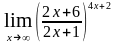 ;
б)
;
б)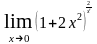 .
.
8. Найти предел функции, используя принцип замены
эквивалентных бесконечно малых функций:
а)
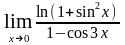 ;
б)
;
б)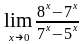 ;
;
в)
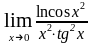 г)
г)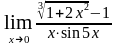
Домашнее задание 3
1. Используя ( - ) определение предела функции в точке,
доказать, что
а)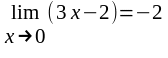 ; б)
; б)
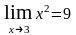 ;
в)
;
в)
 .
.
Указать ().
2. Найти предел функции:
а)
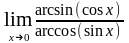 ;
б)
;
б)
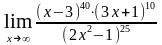 ;
;
в)
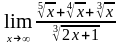 ;
г)
;
г)
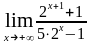 ;
;
д)
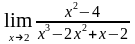 ; е)
; е)
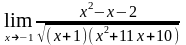 ;
;
ж)
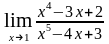 ;
з)
;
з)
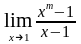 ;
;
и)
 ;
к)
;
к)
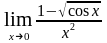 ;
;
л)
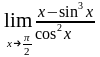 ;
м)
;
м)
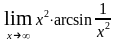 ;
;
н)
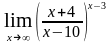 ;
о)
;
о)
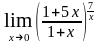
3. Найти предел функции, заменяя бесконечно малые
эквивалентными:
а)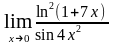 ;
б)
;
б)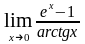 ;
;
в)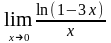 ;
г)
;
г)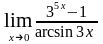 ;
;
д)
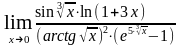
е)
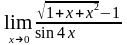 ;
ж)
;
ж)
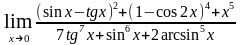 .
.
Тема 4 Непрерывные функции. Точки разрыва функции. Задачи для практического занятия
1. Найти точки разрыва функции:
а)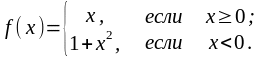 б)
б)
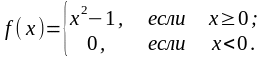
в)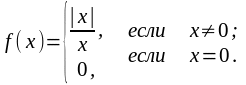
Определить скачок функции в каждой точке разрыва
и построить график.
2.
Исследовать функцию
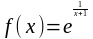 на непрерывность
на непрерывность
в точке xо = 1.
3.
Исследовать
функцию
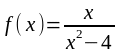 на непрерывность.
на непрерывность.
4.
В
каких точках
имеют разрывы функции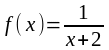 и
и
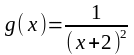 ?
Выяснить разницу в поведении функций
?
Выяснить разницу в поведении функций
вблизи точек разрыва.
5.
Функция
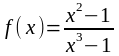 не определена в точке x
= 1.
не определена в точке x
= 1.
Каким должно
быть
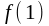 ,
чтобы функция,
,
чтобы функция,
доопределённая таким образом стала непрерывной?
6.
Функции
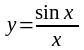 и
и
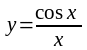 не определены в
не определены в
точке x = 0. Указать характер графиков этих функций
в окрестности точки x = 0.
7. Сколько точек разрыва ( и какого рода) имеет
функция
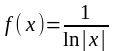 ?
?
8. При каких значениях параметров а и b функция
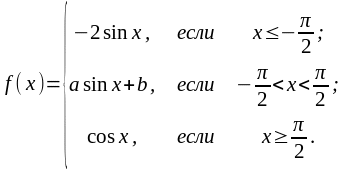
является непрерывной.
