5. Скалярний добуток векторів.

Означення 17. Скалярним добутком векторів називається число, що дорівнює добутку довжин цих векторів на косинус кута між ними: (5.1)

Властивості скалярного добутку.

1.

2.

3.

4.

Теорема 5

Два вектори перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.

Теорема 6

Якщо два вектори задано координатами ( ), то скалярний добуток обчислюється за формулою:

(5.2)

Теорема 7

Косинус кута між векторами обчислюється за формулою: (5.3 )

Приклад 4

У трикутнику з вершинами А(2, -1, 3) , В( -2, 2, 5), С ( 1, 2, 3 ) знайти косинус кута при вершині А.

Розв’язання.

1. Знайдемо координати векторів .

2. Обчислюємо косинус кута за формулою (5.3):

6. Векторний добуток векторів.

Означення 18. Векторним добутком векторів і називається третій вектор , що задовольняє таким умовам:

1.

2.

3. вектори утворюють праву трійку.

Зауваження: вектори утворюють праву трійку, якщо найкоротший поворот від вектора до вектора з кінця вектора спостерігається проти годинникової стрілки.

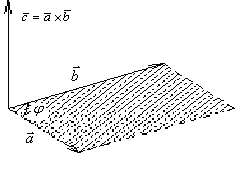
Векторний добуток позначається або [ , ].

Властивості векторного добутку:

1. = -( ) (антикомутативний закон).

2. ( ) = ( ), R (асоціативний закон)

3. ( + ) = + (дистрибутивний закон)

4.

Теорема 8

Якщо , то == , тобто записується за допомогою визначника третього порядку. (6.1)

Приклад 5

Знайти векторний добуток векторів

Розв’язання

За формулою обчислення векторного добутку (6.1)

=

Теорема 9

Для того, щоб вектори були колінеарні, необхідно і достатньо, щоб = 0 або .

Теорема 10

Площа S₁ паралелограма та площа S₂ трикутника, побудованих на векторах і , обчислюються за формулою: S₁= , (6.2)

S₂ = . (6.3)

Приклад 6

Задано вектори Обчислити площу паралелограма, побудованого на векторах і перевірити, чи колінеарні ці вектори.

Розв’язання

1. За формулою (6.1) обчислюємо векторний добуток =

2. Обчислюємо модуль вектора , тому площа паралелограма ( кв.од.)

3. Вектори не колінеарні, бо

7. Мішаний добуток векторів.

Означення 19. Мішаним добутком векторів називається скалярний добуток вектора на вектор , тобто ( ) .

Властивості мішаного добутку:

1. ( ) = -( ) .

2. ( ) = ( ).

Завдяки цій властивості мішаний добуток записується у вигляді ( ) або .

3. ( ) = ( , , ) = ( , , ) = -( , , ) =

= -( , , ) = -( )

Теорема 11

Мішаний добуток векторів, що задані своїми координатами, тобто

,

обчислюється за формулою: ( ) = 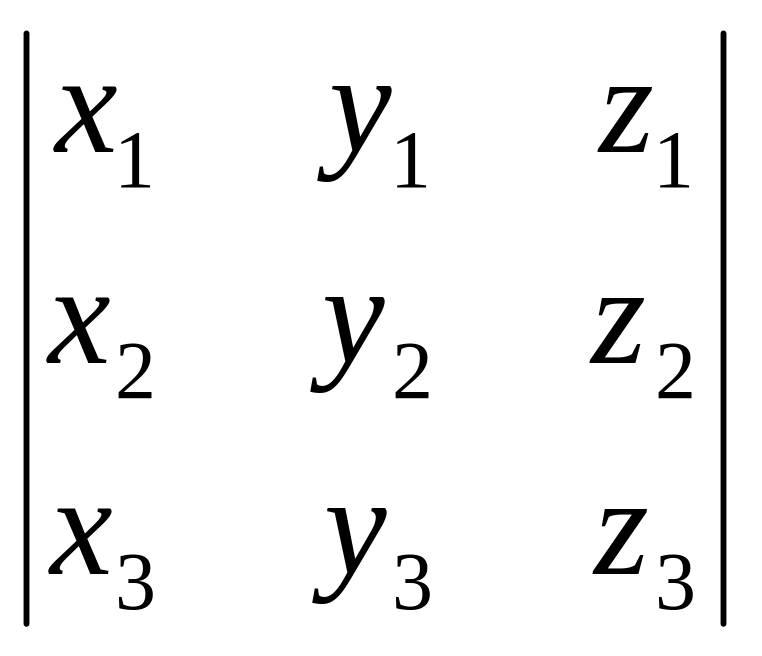. (7.1)

Теорема 12

Для того, щоб вектори були компланарними, необхідно і достатньо, щоб ( ) = 0 або = 0.

Об’єм V₁ паралелепіпеда, побудованого на векторах та об’єм V₂ утвореної цими векторами трикутної піраміди знаходяться за формулами: V₁= (7.2)

V₂ = (7.3)

Приклад 7

Задано вектори

Визначити:

• мішаний добуток векторів ;

• об’єм паралелепіпеда, побудованого на цих векторах;

• перевірити, чи компланарні вектори ;

Розв’язання

1. Мішаний добуток обчислимо за формулою (7.1) =

2. Об’єм паралелепіпеда V₁ =

3. Вектори - не компланарні, бо .

Приклад 8

Задані вершини трикутної піраміди:

Знайти її об’єм.

Розв’язання

1. Знайдемо координати векторів з початком у точці А.

2. Обчислюємо мішаний добуток:

3. Обчислюємо об’єм піраміди за формулою (7.1)

V_п =

III. Завдання для самостійної роботи.

1. Розкласти вектор за базисом

2. Задано вектори Обчислити:

3. Визначити, за якого значення вектори та перпендикулярні.

4. Визначити довжину діагоналей паралелограма, побудованого на векторах , якщо відомо, що та кут між векторами .

5. Знайти координати вектора , колінеарного вектору і такого, що задовольняє умові

6. Вектор , перпендикулярний вектору та вектору задовольняє умові Знайти координати вектора .

7. , кут між векторами . Обчислити площу трикутника, побудованого на векторах

8. Обчислити площу трикутника з вершинами А(1,1,1), В(2,3,4), та С(4,3,2).

9. Встановити, чи утворюють вектори базис у множині всіх векторів, якщо

10. Обчислити об’єм паралелепіпеда побудованого на векторах:

11. Обчислити об’єм піраміди , якщо

12. Обчислити об’єм піраміди з вершинами у точках

А(2,-3,5), В(0,2,1), С(-2,-2,3) та D(3,2,4).

13. У піраміді з вершинами у точках А(1,1,1), В(2,0,2), С(2,2,2) і D(3,4,-3) обчислити висоту

14. Перевірити, чи компланарні задані вектори:

15. Визначити значення , за яким вектори будуть компланарні, якщо

.

16. Довести, що чотири точки А(1,2,-1), В(0,1,5), С(-1,2,1) і D(2,1,3) лежать в одній площині.

IV. Завдання контрольної роботи.

Завдання 1

Задані вектори . Визначити:

1. Довжину вектора ;

2. Скалярний добуток векторів та ;

3. Векторний добуток векторів та ;

4. Площу паралелограма, побудованого на векторах та ;

5. Мішаний добуток векторів ;

6. Об’єм паралелепіпеда, побудованого на векторах ;

7. Чи колінеарні вектори та ;

8. Чи компланарні вектори ;

Варіанти завдань:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17.

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

26. ;

27. ;

28. ;

29. ;

30. ;

31.

32.

33.

Завдання 2

Перевірити, що вектори утворюють базис. Написати розклад вектора за цим базисом.

Варіанти завдань:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

Завдання 3

Задані вершини трикутної піраміди А, В, С і D. Обчислити об’єм піраміди.

Варіанти завдань:

1. A (3, 4, 5), 2. A (-7, -5, 6),

3. A (1, 3, 1),

4. A (2, 4, 1),

5. A (-5, -3, -4),

B (-2, 5, -3),

B (-1, 4, 6),

B (-3, -2, 4),

B (1, 4, 6),

B (-2, 3, -5),

C (3, -2, 4),

C (-2, -3, 4),

C (3, 5, -2),

C (3, 2, -2),

C (4, -3, 6),

D (1, 2, 2);

D (3, 4, -4);

D (4, 2, -3);

D (8, -2, 4);

D (6, -5, 3);