В общем виде алгоритм запишется:

i - текущая итерация.

Процесс итераций по x следует повторять до достижения величиной заданной точности ε. Предыдущее и последующее значения x будут совпадать с точностью до ε.

Кроме значения функции f(x_i ) требуется знать производную в текущей точке.

Получим ее, записав уравнение (1.11) в виде: где

Продифференцируем f(x), получим:

Пусть х=х_о, тогда, т.е. полином, пониженного на единицу порядка, является производной от исходного полинома.

Если использовать рекуррентное соотношение (1.16), то, продифференцировав его, получим следующий алгоритм:

присвоим

и в цикле считаем (1.18)

Объединив алгоритмы (1.16)-(1.18), реализуем их на МATLAB:

function [x]=newtonR;

global f x;

xа =-1.2; eps=0.0001;

for m=1:20

[f]=gornerR;

x=x-f;

if (abs(f)<eps),break,end

end

function [f]=gornerR;

global f x

n=3; a=[1 3 3 1]; y=a(1); y1=0 ;

for k=2:n+1

y1=y+x*y1;

y=a(k)+x*y;

end

f=y./y1;

При обращении из МATLAB [x]=newtonR получим значение корня x = -1.0001.

В m-файле newtonR имеется две возможности остановить итерации: задавая параметр цикла 20, либо по условному оператору if. Количество итераций можно определить более простыми методами. Попробуйте это сделать самостоятельно.

Если все корни вещественные, то, использовав процедуру понижения порядка, можно определить новый корень и т.д. до тех пор пока порядок уравнения не будет равным 2. Решение квадратного уравнения позволит определить два оставшихся корня.

Весьма полезным для работы с полиномами является следующий m. файл:

function [s]=SumPoly(p,q)

%Определяется сумма векторов p и q. Они должны быть заданы

%Определяется длина векторов р и q и выбирается большая из них

max1=max(length(p),length(q));

%Фиксирутся длина нулевых векторов p1 и q1

p1=zeros(1,max1);

q1=zeros(1,max1);

%Формируются векторы p1 и q1 равной длины

p1(max1-length(p)+1:max1)=p;

q1(max1-length(q)+1:max1)=q;

s=p1+q1;

Задаем исходные полиномы произвольного порядка p и q: p=[1 1 1 1 1];q=[2 2 2 2 2 2];

s – алгебраическая сумма полиномов: s =[2 3 3 3 3 3]. При составлении собственных программ преобразования передаточных функций приемы программирования, использованные в данном m.файле, могут оказаться очень полезными.

Умножение полиномов происходит с помощью оператора [a]=conv(p,q). Результат a – вектор коэффициентов полинома произведения.

Деление полиномов с помощью оператора [a,b]=deconv(p,q). Целая часть – а, коэффициенты полинома числителя остатка деления – b.

Коэффициенты полиномов можно определить по корням уравнения с помощью оператора poly(x).

Для счета функций можно использовать стандартные операторы eval и feval. Например, eval(‘x.^3+x.^2+x+1’) и feval(‘func’,1). В первом случае предварительно следует задать x = 1, а во втором запасти в func.m файле необходимую функцию и задать значение аргумента. Функция может зависеть от многих переменных.

Задание для самостоятельной работы:

Реализовать на МATLAB решение алгебраических уравнений

а) ,

б) ,

в) , т.е. определить все корни.

г) Дать пояснения для операторов SumPoly(p,q).m файла.

д) Поработать с операторами conv, deconv, poly, eval, feval.

Рассмотрим общий случай, когда корни уравнения (1.10) комплексные.

Обозначим и рассмотрим применение схемы Горнера к расчету полинома f(x). Подставив комплексный корень в f(x), мы получим комплексную функцию f(x₁,x₂). Вещественную часть функции обозначим y₁, а мнимую y₂, т.е. y=f(x)=y₁+jy₂ .

Запишем схему Горнера, используя (1.16) следующим образом:

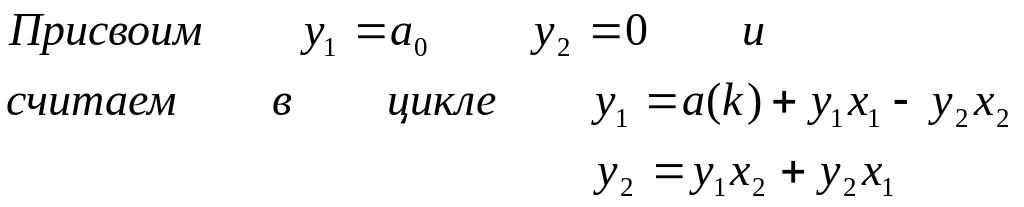(1.19)

Рассмотрим алгоритм расчета производной для комплексного x с использованием схемы Горнера. Обозначим вещественное значение производной F₁, а мнимое значение F₂. Дифференцируя соотношения (1.19), получим рекуррентные соотношения:

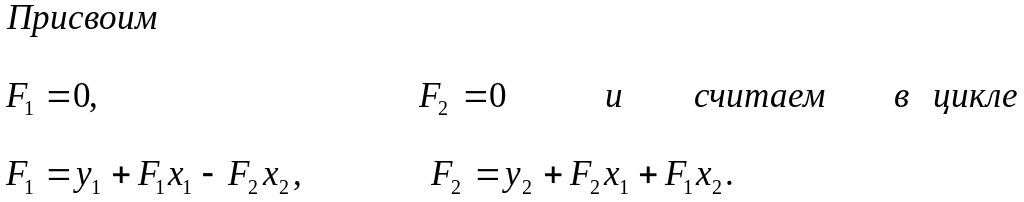(1.20)

Алгоритмы расчета y=f(x) и для комплексных корней получены. Используем их для алгоритма Ньютона (1.17). Если отношение к привести к алгебраической форме записи, то получим два уравнения:

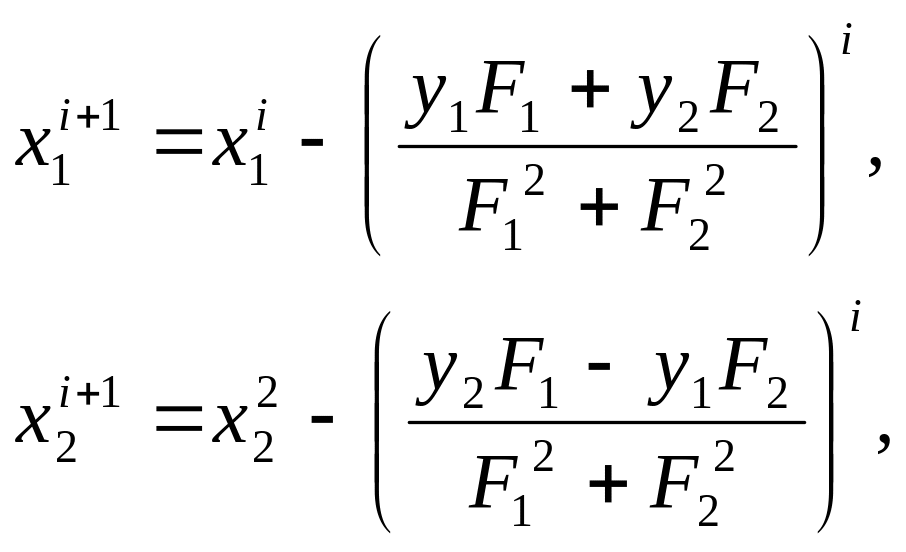(1.21)

которые позволяют определить вещественную и мнимую части искомого корня . Итерации обозначены индексами i.

В представленных далее m.файлах использованы полученные алгоритмы, но с помощью их решение можно получить лишь для одного корня. Необходимо самостоятельно реализовать алгоритмы для определения всех корней алгебраического уравнения для приведенного далее примера. Требуется также объяснить причины возникающих при этом трудностей.

function [y,f]=gornerC;

%Расчет полинома по схеме Горнера для комплексных корней

% %y(1)-вещественная часть полинома,y(2)-мнимая часть полинома,

%f(1)-вещественная часть производной от полинома,

%f(2)-мнимая часть производной от полинома.

global F x;

n=4; a=[1 5 10 10 4];

y(1)=a(1); y(2)=0; f(1)=0; f(2)=0;

for k=2:n+1

R(1)=y(1)+x(1)*f(1)-x(2)*f(2);

f(2)=y(2)+x(1)*f(2)+x(2)*f(1); f(1)=R(1);

R1(1)=a(k)+x(1)*y(1)-x(2)*y(2);

y(2)=x(1)*y(2)+x(2)*y(1); y(1)=R1(1);

end;

%Вещественная часть отношения функции к производной от нее в алгоритме

%Ньютона F(1) и F(2)-мнимая часть.

F(1)=y(1)*f(1)+y(2)*f(2);

F(2)=y(2)*f(1)-y(1)*f(2);

%Знаменатель

Zn(1)=f(1)^2+f(2)^2;

%Отношение

F(1)=F(1)/Zn(1); F(2)=F(2)/Zn(1);

function [x]=newtonC;

%Расчет комплексного сопряженного корня методом Ньютона

%Обращение из командной строки [x]=newtonC

global F x;

x(1)=-1.2; x(2)=1.0; eps=0.001;

;%Для цикла с предусловием необходимо задать заведомо неприемлемые значения

F(1)=10; F(2)=10;

%Далее следуют два варианта заданной точности счета

while sqrt(F(1)*F(1)+F(2)*F(2))>eps % abs(F(1)+F(2))>eps

[F]=gornerC;

x(1)=x(1)-F(1);

x(2)=x(2)-F(2);

end

Идентификаторы F1 и F2 использовали в файле gornerC.m дважды.

Значения этих параметров из файла gornerC.m передаются в файл newtonC.m (1.21).

Для комплексных сопряженных корней х=х₁ jх₂ запишем квадратное уравнение:

x² + рx + q = 0,

где p = - 2x₁, q =x₁² +x₂².

Поэтому исходное уравнение (1.10) можно записать в виде:

y(x) = (x² + px + q)(b_n-2 + b_n-3x+…+b₁x^n-3 + b₀x^n-2), (1.22)

если x=x₁  jx₂ – корни исходного полинома y(x).

Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях x у исходного (1.10) и правого полиномов (1.22) получим:

b₀ = a₀,

b₁ = a₁ - pb₀

b₂ = a₂ - pb₁ - qb₀

……………….

b_n-2 = a_n-2 - pb_n-3-qb_n-4

Коэффициенты определяются рекуррентно. Запишем полученный алгоритм в виде процедуры:

function [a,b]=ponporC;

%Заданы размер вектора коэффициентов полинома n и значение комплексного корня

% x(1)+-j x(2)

%Получили вектор коэффициентов b для полинома степени n-2 и запасли его в вектор a

%%Обращение из командной строки [a,b]=ponporC

n=5; a=[1 4 7 6 2]; b=zeros(1,n);

x(1)=-1; x(2)=1;

b(1)=a(1); p=-2*x(1); q=x(1)^2+x(2)^2;

b(2)=a(2)-p*b(1);

for k=3:n-2

b(k)=a(k)-p*b(k-1)-q*b(k-2);

end;

for k=1:n-2

a(k)=b(k);

end

for k=n:-1:n-1

a(k)=[];

end

Таким образом, мы имеем в распоряжении алгоритмы, которые позволяют определить корни характеристического уравнения.

Сходимость метода Ньютона зависит от выбора начального приближения для искомого корня. Точность определения корней ε задается. Обычно используется неравенство . Точность может быть задана и в относительных величинах. Можно задавать точность определения искомого корня

Недостатки метода Ньютона.

Наличие в знаменателе алгоритма Ньютона производной приводит к тому, что для кратных корней одновременно и

y = f(x), и равны 0. Аналогичная ситуация может возникнуть для пары близко расположенных корней.

Возможно также зацикливание итераций. Эти варианты показаны на рис 1.2 а) и б).

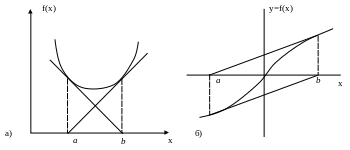
а) б)

рис.1.2

Задавая начальное приближение по x в точке a и, в соответствии с алгоритмом Ньютона, двигаясь по касательной к кривой, попадаем в точку b. Откуда, по касательной к кривой, вновь приходим в точку a. Происходит «зацикливание» алгоритма расчета.

Поэтому алгоритм Ньютона работает не всегда. В таких случаях говорят, что метод не сходится.

Задание для самостоятельной работы:

Реализовать на МATLAB решение алгебраических уравнений

а) ,

б) ,

в) ,

г) ,

д) , т.е. определить все корни.

Рассмотрим метод решения алгебраических уравнений, который хорошо работает при наличии кратных корней.

1.4. Метод Бэрстоу.

Метод удобен для уравнений четной степени и дает возможность определять любые корни (действительные или комплексные). Введем в рассмотрение уравнение

x² - p x – q = 0. (1.23)

Метод Бэрстоу позволяет определить итерациями значения p и q. Решив квадратное уравнение (1.23), можно понизить порядок исходного уравнения и повторить алгоритм определения p и q. Приведем алгоритм определения p и q без доказательства:

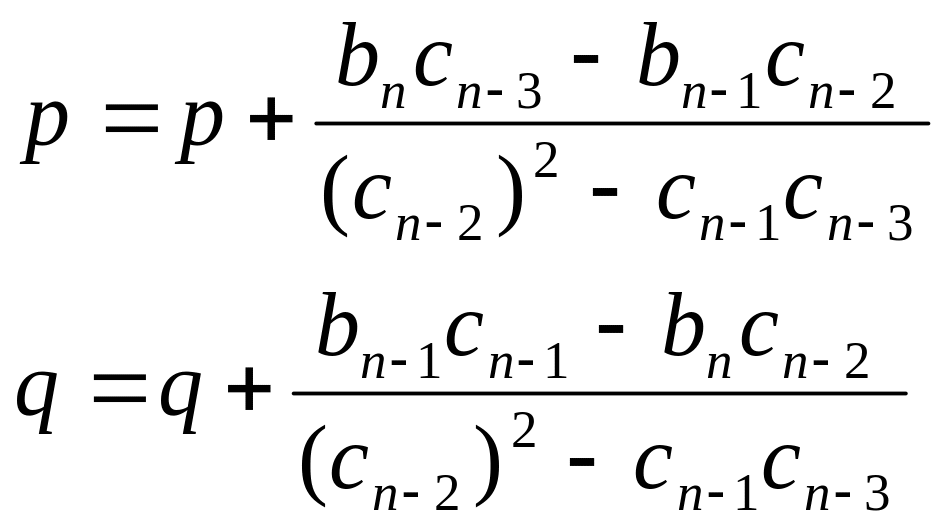, (1.24)

где коэффициенты b и c определяются так:

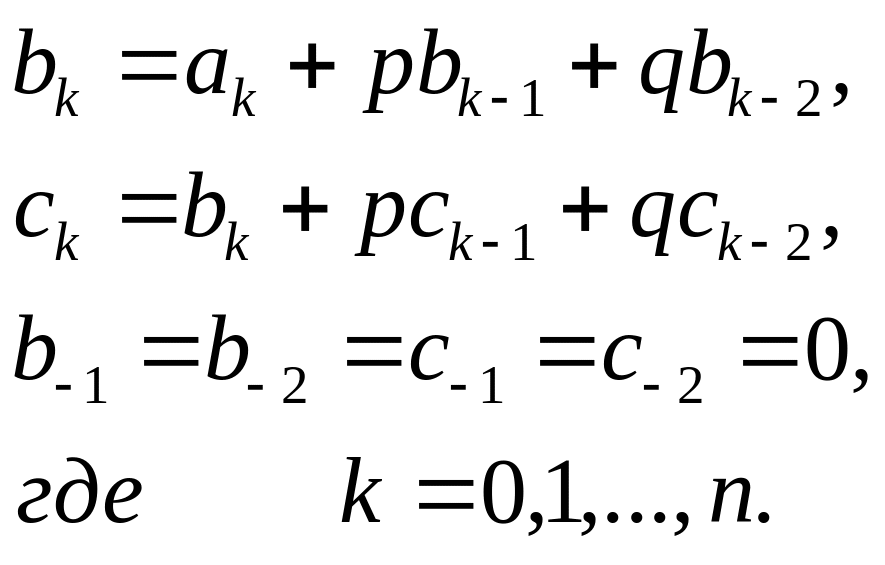(1.25)

Сначала в цикле определяются коэффициенты b и c, а затем производится расчет коэффициентов p и q. Итерации повторяются до тех пор пока второе слагаемое (1.24) не будет меньше по модулю заданного значения ε.

Для комплексных корней сходимость метода Бэрстоу лучше, чем метода Ньютона. Имеется программа на Турбо Паскале, реализующая метод Бэрстоу для алгебраического уравнения произвольного порядка. Желающие могут ее получить.

Перечислим существующие наиболее известные методы:

- метод Мюллера - рекомендуется для тех же случаев, что и метод Бэрстоу;

- метод Лобачевского – позволяет определить сначала действительные и чисто мнимые корни;

- метод Бернулли – дает приближение сразу по всем корням;

- матричные методы.

Такой арсенал методов говорит о серьезности проблемы и о попытках известных ученых разработать универсальный метод.

Задание для самостоятельной работы:

Реализовать на МATLAB решение алгебраических уравнений методом Бэрстоу

а) ,

б) ,

в) , т.е. определить все корни.

МATLAB располагает программами, позволяющими решить алгебраическое уравнение с помощью оператора roots(a), где а вектор коэффициентов характеристического уравнения.

Например, a=[1 3 3 1]; roots(a).

Для работы с передаточными функциями (ПФ) полезно знание следующих простых стандартных операторов.

b=[0 0 0 1]; a=[1 3 3 1];

% векторы коэффициентов числителя и знаменателя ПФ

w = tf(b,a);

% ПФ в стандартной форме

p=pole(w); z=zero(w);

% вычисление нулей и полюсов

pzmap(w);

% построение нулей и полюсов на комплексной плоскости.

Некоторые из перечисленных методов позволяют решать и нелинейные уравнения общего вида f(x) = 0.

Аналитических методов решения даже отдельного нелинейного уравнения общего вида не существует. Галуа Эварист доказал, что уравнения 5-й степени и нелинейные уравнения не имеют аналитического решения. Поэтому уравнения высоких степеней и нелинейные можно решить лишь численными методами. Отсюда и некоторая условность их решения, а часто возникает тупиковая ситуация, т.е. решение отсутствует. Причиной может быть плохой алгоритм или использование машинной арифметики. Приведем простейшие примеры.

Уравнение не имеет решения, а уравнение имеет сколько угодно решений.

В случае системы нелинейных уравнений проблема поиска решений обостряется многократно.

В задачах динамики при рассмотрении реальных нелинейных математических моделей объектов управления (ОУ) такие задачи встречаются часто.

, (1.26)

где x и f - векторы с n компонентами.

Чтобы выполнить интегрирование системы нелинейных дифференциальных уравнений (1.26), необходимо задать начальные условия, т.е. при t = 0 задать такие x = x₀ , которые обеспечат по окончании переходного процесса установившийся режим работы. В этом случае и можно утверждать, что решена система уравнений

f(x) = 0. Но этот способ редко используется для решения сложных задач: он мало эффективен.

Отметим принципиальное сходство задачи решения системы нелинейных уравнений и задачи оптимизации, т.е. поиска экстремума функций. Действительно формально задачи решения систем f(x) = 0 и мало чем отличаются.

Однако, методы их решения развиваются независимо друг от друга. Отсутствие универсальных алгоритмов решения этих задач подчеркивает трудность их решения даже при небольших n. В отдельных прикладных приложениях приходится заниматься теоретической и экспериментальной «доводкой» методов решения таких задач.

Рассмотрим некоторые методы решения нелинейных уравнений. Речь будет идти о вещественных корнях отдельного нелинейного уравнения.