33

Численные методы

3 курс, 5 семестр

1. 24 часа лекции + 12 часов практические занятия.

2. Курсовой проект.

3. Экзамен после выполнения курсового проекта.

Список литературы

1. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. -

М.: Мир, 1977.

2. Корн Г., Корн Т. Справочник по математике, глава 20-я, М.: Наука , 1978.

3. Калиткин Н.Н. Численные методы. – М.: Наука, 1978.

4. Турчак Л.И. Основы численных методов. – М.: Наука, 1987.

5. Банди Б. Методы оптимизации. – М.: Наука, 1987.

6. Волков Е.А. Численные методы. – М.: Наука, 1987.

7. Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для

персональных ЭВМ. – М.: Наука, 1989.

8. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. –

М.: Роско,1991.

9.Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Физматгиз, 2001.

10. Метьюз D. Численные методы.- М.: 2000.

Ряд вычислительных или асимптотических методов вошли в теорию по именам их

Создателей: методы Ньютона, Эйлера, Лобачевского, Гаусса, Чебышева, Эрмита, Крылова.

В России в настоящее время наиболее известны имена: академиков Тихонова А.Н., Самарского А.А., Марчука А.И.

За рубежом это: Хемминг Р.В., Вазов В., Дж. Форсайт, Милн В.Э., Пауэлл М.,

Давидон В.К., Флетчер Р.

Основоположники вычислительных методов Эйлер, Ньютон и Гаусс. Их идеи были востребованы через 100- 200 лет с появлением ЭВМ, созданных для проведения трудоёмких научных расчётов при проектировании сложных ракетных комплексов, ядерных устройств, энергетических установок и летательных аппаратов.

В свою очередь ЭВМ стимулировали бурный рост вычислительной математики и методов математического моделирования различных технологических устройств и процессов. Разработка и проектирование немыслимы, в современных условиях, без проведения серьёзных расчётных исследований. Расчётный эксперимент позволяет заменить более дорогие, а часто и практически невозможные натурные эксперименты. Тем не менее единственным критерием расчётных исследований является реальный эксперимент. Любое самое сложное устройство после проектирования будет работать,

если расчетные эксперименты проведены на достоверных математических моделях,а

задача грамотно сформулирована и решена.

Постараемся определить место вычислительной математики в работе инженера.

Исследователей в области:

1. Фундаментальных наук готовят МГУ, МФТИ и МИФИ, т.е. вузы с ярко выраженной теоретической подготовкой. Более прикладными областями технических знаний занимаются такие вузы как МВТУ, МАИ, МГАПИ и др. которые имеют очевидные признаки ведомственной принадлежности.

2. Все поисковые и прикладные исследования происходят в ведомственных НИИ, которые занимаются расчётными и экспериментальными работами.

3. Группы ОКБ занимались конструкторской проработкой и конкретными расчётами опытных образцов, которые изготовляли на опытных заводах при ОКБ. Проводились экспериментальные исследования опытных образцов совместными усилиями ОКБ и НИИ

4. А затем опытное изделие передавалось серийным заводам и СКБ. Организовывался процесс производства с технологической подготовкой.

5. Эксплуатация изделий с подготовкой правил эксплуатации, обслуживания и ремонта.

Все указанные периоды создания изделий требуют использования инженерного труда. Серьёзная расчётная работа ведется в НИИ и ОКБ. Поступление в аспирантуру

и ее окончание может вывести инженера на уровень п.1.

Что требуется от инженера-расчётчика?

(Более классическое название инженер-исследователь)

1. Умение работать на ЭВМ:

Знание возможностей операционной системы и транслятора, владение алгоритмическими

языками, работа с “оболочками” и современными программными продуктами.

2. Знание численных методов:

а) классических методов весьма обширной и бурно развивающейся вычислительной математики,

б) специальных методов теории автоматического управления (ТАУ) в её классической

и современной областях.

Часть этих знаний приобретается студентами за время обучения в вузе. И их следует рассматривать как начальное условия для дальнейшей плодотворной работы. Лавинный рост знаний приводит к быстрому их старению. Поэтому без солидного фундамента знаний невозможно обеспечить движение науки вперед.

Выбор численных методов в данном цикле лекций предполагает крен в сторону методов, наиболее пригодных для исследования систем управления, т.е. для дисциплин изучаемых на старших курсах.

Источники ошибок при вычислениях на ЭВМ.

1.Неточность математического описания задачи и в частности неточность задания исходных данных.

Пример.

Задача.

Определить время, за которое самолет преодолеет расстояние от А до В.

Он движется со скоростью 800 км/ч на высоте 8000 км.

Скорость и направление ветра на всем пути неизвестны.

2.Конечное число значащих цифр (двоичных разрядов в микропроцессоре ЭВМ)

Пример.

Задача.

Решить квадратное уравнение:

,

р ешение получено для меньшего корня и четырехзначных десятичных цифр, участвующих в расчётах:

Более точное решение:

Особенно внимательно следует относится к малым разностям, которые попадают в знаменатель любого выражения. Необходимо алгебраическими преобразованиями избавится от малых разностей в противном случае результат будет не предсказуемым.

3.Ошибки округления.

Фактически зависят от количества значащих цифр, используемых в ЭВМ. Округление

может выполнятся отбрасыванием младших разрядов или округлением с точностью

до 0,5. В ЭВМ округление производится для двоичных чисел ( и где t- число значащих цифр) .

4. Ошибки ограничения.

Определяются методом вычисления

Бесконечный вычислительный процесс заменяется конечным.

Таким образом, 1 - погрешности неустранимые,

2,3 - погрешности вычислительные,

4 – погрешности метода.

Ошибки относительные и абсолютные.

, где - абсолютная ошибка,

- точное решение,

х – приближенное, реально полученное решение,

- относительная ошибка

Величины ошибок при совершении конкретных действий оцениваются с помощью

дифференциала. Важно понять распространение ошибок в ходе вычислений. Эта

проблема в общем виде не разрешима.

Оценка абсолютных ошибок при арифметических действиях:

- сложение, вычитание.

- умножение.

- деление.

Оценка относительных ошибок при арифметических действиях:

- сложение и вычитание,

- умножение.

- деление.

При необходимости приведённые формулы абсолютных и относительных погрешностей

можно использовать в проверочных расчётах. Трудоёмкость таких оценок очевидна.

Общие рекомендации.

1. Необходимо минимизировать число арифметических операций.

2. Следует избегать вычитания двух почти равных чисел в знаменателе любого

выражения.

3. Сначала следует проводить вычисления с меньшими числами.

Практическое вычисление функций.

Обычно все элементарные функции: sin x, cos x, ln x, и т.д. вычисляются с помощью

рядов. Особенностью разложения в ряд Тейлора является рост ошибки с ростом х

вблизи точки х=1, хотя сама по себе ошибка ограничения может быть очень малой. При

разложении элементарных функций в ряд с помощью полиномов Чебышева можно

минимизировать ошибку в диапазоне 0<x<1. Но использование этих полиномов

приводит к более сложным выражениям.

Обычная структура ряда ( Тейлора, Чебышева) может быть предоставлена в виде:

(1)

Во многих практических приложениях ряд записывается иначе :

(2)

Сразу же запишем алгоритм преобразования коэффициентов:

, где n-степень полинома, а

Использование цикла позволит преобразовывать коэффициенты. Необходимо уделить

внимание таким полиномам. В ТАУ одна из основных форм математических моделей

систем управления записывается в общем виде так:

(3)

т.е. в виде отношения 2-х полиномов (1). А поскольку функции вида называются

целыми рациональными полиномами, а (3) – дробно-рациональными функциями. Обычно

коэффициенты полиномов – вещественные числа, а степени – целые числа. Если

приравнять полином числителя или знаменателя нулю, то получим алгебраическое

уравнение:

(4)

Основные свойства уравнения (4):

Число корней равно n, корни могут быть нулевыми, вещественными, мнимыми сопря-

жёнными и комплексными сопряжёнными числами, равные корни называются

кратными и учитываются при подсчёте корней. Нечетная степени означает, что, по крайней мере, один корень вещественный. Любой корень по модулю не превосходит

числа ,

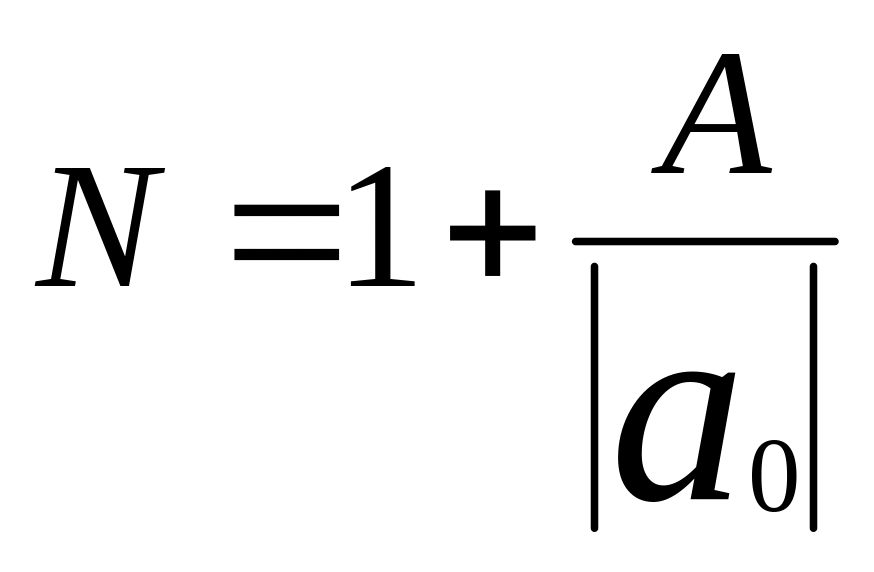где А наибольшее из чисел:

Необходимое условие отрицательности всех корней уравнена (4)- положительность его коэффициентов

• Поскольку корни уравнения (4) являются нулями функции f(x), то непосредственной подставкой Х можно в интервале a<x<b определить число пересечений f(x) оси абсцисс. Так можно определить все действительные корни уравнения, если просмотреть всю числовую ось Х-Х.

• Если f(a) и f(b) одного знака, то возможное число корня в интервале a<x<b - четно. При просмотре числовой оси Х-Х недостающее число корней соответствует комплексным сопряженным, а поэтому всегда четно.

Основная теорема алгебры

f(x) = a₀(x-x₁)(x-x₂)…(x-x_n) = 0, (5)

где x₁, x₂, x3,…, x_n - корни уравнения (4).

В ТАУ оно называется характеристическим (знаменатель W(p)).

1. Необходимое и достаточное условие устойчивости системы – это отрицательность всех вещественных частей корней характеристического уравнения

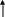j

2. Корни характеристического уравнения необходимо знать для того, чтобы записать аналитическое решение дифференциального уравнения, для которого получено характеристическое уравнение:

где .

Пусть

а поскольку , то получили характеристическое уравнение:

Аналитическое решение можно получить для алгебраического уравнения до 4-го порядка. Справочники по математике содержат эти методы.

Для уравнений более высокого порядка таких методов нет. Зато существуют вычислительные методы:

Рассмотрим наиболее распространенные численные методы решения уравнений вида (1):

Но для этого введем в рассмотрение схему Горнера, позволяющую наиболее экономно вести вычисление полинома f(x). Пусть

(6).

т.е. слева полином вида (1).

Раскроем скобки справа и приравняем коэффициенты при одинаковых степенях Х:

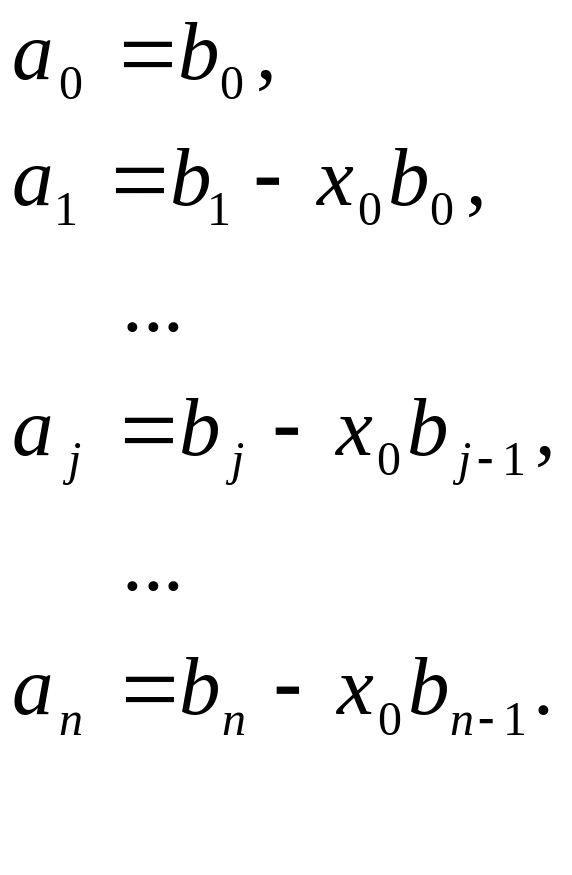
Перепишем в рекуррентном виде относительно введенных в рассмотрение (неизвестных) коэффициентов :

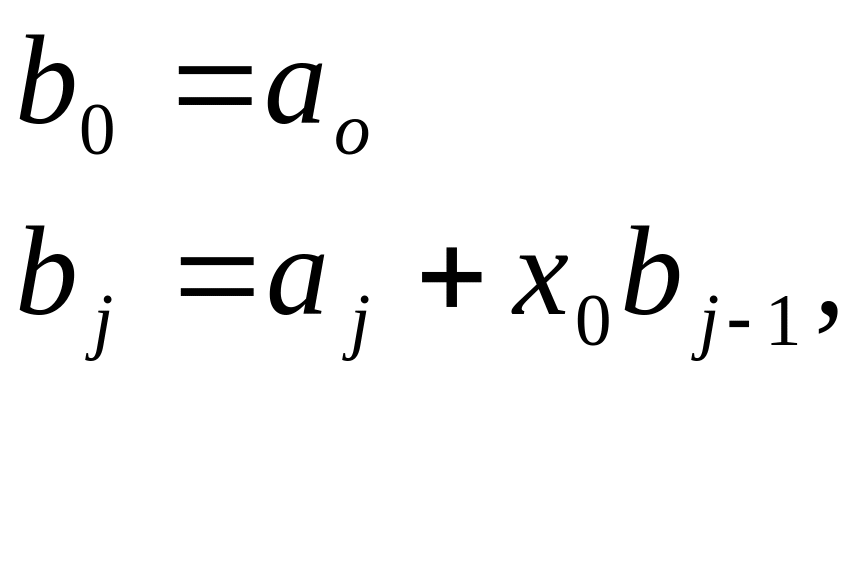где j=1, 2,…,n (7)

Рассмотрим пример для n=5.

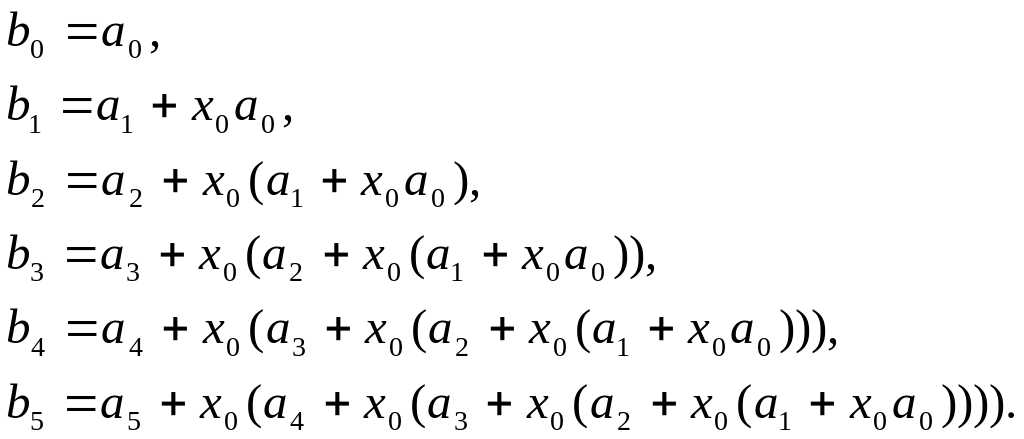
Как это видно из уравнения (6) и из рассмотренного примера т.е. следовательно, мы доказали теорему Безу. Представим уравнение (6) в виде: 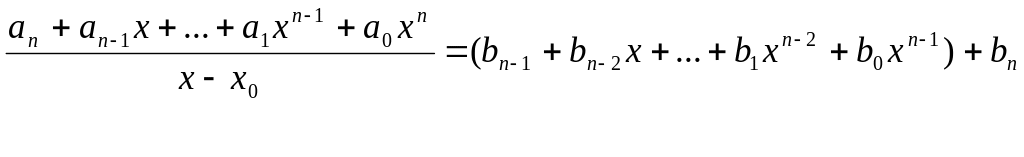, b_n – остаток от деления, а выражение в скобках – частное.

Величина х₀ взята произвольно, поэтому если х₀ -корень уравнения (1), то b_n=0, т.е. деление будет произвольно без остатка, кроме того, получена формула (7) понижения порядка исходного номинала (1), если известен корень уравнения (1) - вещественный.

Т.О., если определен корень характеристического уравнения, то можно понизить на единицу степень полинома и приступить к решению уравнения:

.

И, наконец, также в силу произвольности х₀ мы получим рекуррентную схему вычисления значения f(x) на следующей схеме (Горнера):

Обозначим f(x)=y и запишем схему Горнера по строкам следующим образом:

где условно обозначены одинаковым символом y значения f(x), вычисляемые последовательно, строка за строкой.

Запишем алгоритм вычисления f(x) на языке Паскаль (без описания):

begin Y:=A[0]

for I:=1 to N do

Y:=A[I]+Y+X;

end;

Начальное значение X_о, степень уравнения n и коэффициенты a₀, a₁,…,a_n заданы. Легко подсчитать, что при вычислении по схеме Горнера требуется 2n арифметических действий, а по формуле (1): .

Идентификаторы совпадают для переменных: .

А главное, алгоритм, в силу рекурсивности, весьма экономичен. Уменьшение числа операций уменьшает ошибки округления.

Получим еще один, важный для будущих преобразований, результат, использовав уравнение (6): где

Продифференцируем f(Х), получим:

Пусть х=х_о, тогда, т.е. полином, пониженного на единицу порядка, является производной от исходного полинома.

Продифференцируем последовательно (строка за строкой) соотношения (8):

где у и y’ берутся с предыдущей строки из соотношений (8) и (9).

Полученный результат представим в виде алгоритма на языке Паскаль:

procedure POLINR;

var I: integer;

var Y, Y1: real;

begin Y:= A[0]; Y1:= 0;

for I:=1 to N do

begin Y1:=Y+Y1*X; end;

end;

Идентификатор Y1 соответствует y’. Остальные обозначения сохранены.

Одновременно с помощью процедуры POLINR для заданного Х подсчитываются значения y=f(x) и y’=f’(x).

Схема Горнера также сохранена при расчете y=f(x) и y’=f’(x).

Перейдем к методу Ньютона (решения характеристического уравнения):

Рассмотрим графическую интерпретацию метода:

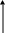f(x) X₀ – начальное приближение.

В точке Х₀ проводим касательную

(производную) до пересечения с осью х-х

в точке Х₁.

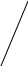f(x₀)

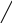
x

^X₂ ^X₁ ^X₀

Приближенное значение производной можно записать: т.К. , то далее процесс итераций х следует повторить до достижения величиной заданной точности е. В общем виде алгоритм запишется :

обычно ограничивается и число итераций.

Если ввести в предыдущий алгоритм обозначения записав его в виде [ F:=Y/Y1; ], то алгоритм метода Ньютона запишется:

procedure NEWTONR;

Const E=1E-6;

var F: real;

begin repeat POLINR; F:=Y/Y1;

X:=X-F;

until abs(F)<E; end;

Аналогичным образом можно решить любое уравнение вида: f(x)=0 (нелинейное, алгебраическое, где f(x)-дифференцируемая функция, имеющие вещественные корни).

Для решения алгебраического уравнения (1), таким образом, получим следующий алгоритм (корни вещественные):

1). Задаются коэффициенты уравнения а₀, а₁,…,а_n и его степень n. Задается начальное приближение

2). Записывается обращение к процедуре NEWTONR, которая содержит обращение к процедуре POLIMR.

3). Полученное значение корня выводится на экран (принтер).

4). Исходная степень полинома понижается на единицу в соответствии с процедурой

procedure PONPOR1;

var I: integer; type t=array[0..10] of real;

var B:t;

begin B[0]:= A[0];

for I:=1 to N-1 do

B[I]:= A[I]+B[I-1];

for I:=1 to N-1 do

A[I]:= B[I];

N:= N-1;

end;

5). И далее п. 2-4 повторяется пока порядок уравнения не понизится до квадратного уравнения, либо до уравнения первого порядка, которые необходимо решить.

Основной недостаток метода очевиден из алгоритма (10):

при наличии кратных корней полинома (1) одновременно стремятся к нулю f(x_i) и f’(x_i) ,а деление на нуль невозможно. Ясно также, что выбор начальных приближений сильно влияет на сходность метода. В случае решения алгебраических уравнений (обычный расчет полинома f(x) в заданном интервале Х и представление f(x) в виде графика) помогает установить структуру корней и их приближенные значения.

В случае нелинейных уравнений такой прием приемлем лишь для одного уравнения.

Корни комплексные (сопряженные)

Обозначим и рассмотрим применение схемы Горнера к расчету полинома f(x) (1) решение уравнения f(x)=0 методом Ньютона.

Как и раньше, распишем схему Горнера по строкам следующим образом, поясняя ее рекурсивность.

Подставив комплексный корень в уравнение (1), мы получим комплексную функцию f(x₁,x₂), вещественную часть функции обозначим y₁, а меньшую y₂, т.е. y=f(x)=y₁+jy₂.

Как и ранее, очередная строка определяется по значениям, подставленным для предыдущей строки. Представим полученный алгоритм в виде следующей процедуры:

procedure POLINC;

var Y1, Y2, R1: real;

var I: integer;

begin Y1:=A[0]; Y2:=0;

for I:=1 to N do

begin R1:= A[I]+ X1*Y1- X2*Y2;

Y2:= X1*Y2+ X2*Y1;

Y1:= R1; end;

end;

Рассмотрим алгоритм расчета производной для комплексного Х с использованием схемы Горнера. Обозначим вещественное значение производной F₁, а мнимое значение F₂. Используя соотношения(9), получим:

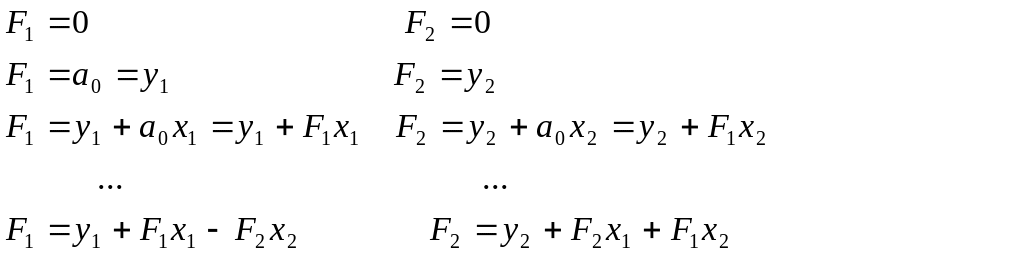
Рекурсивность получена. В предыдущей процедуре получен алгоритм расчета вещественной y₁, и мнимой y₂ частей y=f(x). Но, прежде чем использовать его в очередной процедуре, запишем алгоритм расчета вещественной и мнимой частей алгоритма Ньютона (10). Если отношение и привести к алгебраической форме записи, то получим два уравнения:

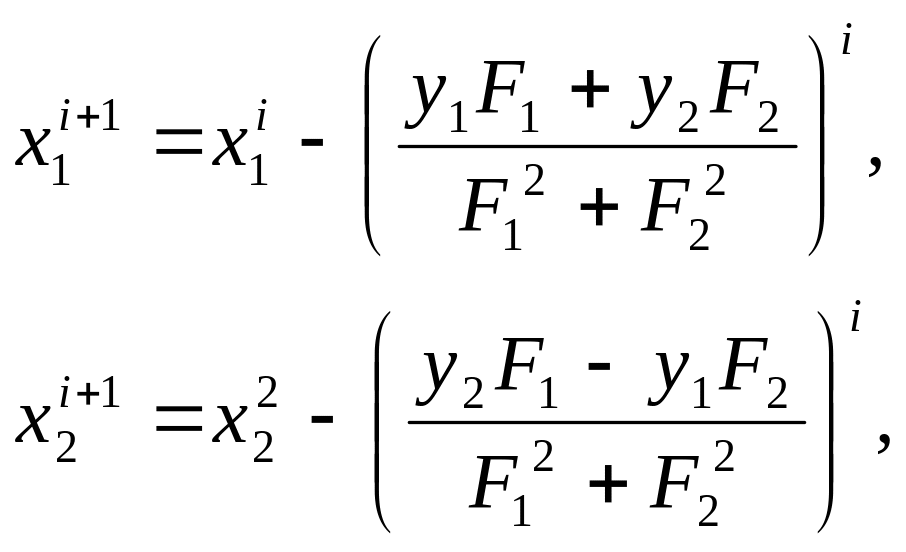
которые позволяют определить вещественную и мнимую части искомого корня

В представленной далее процедуре используем полученные алгоритмы

procedure PolinC;

var Y1, Y2, F1, F2, R1, R2, R, Q :real;

var I :integer;

begin Y1:= A[0]; Y2:= 0; F1:= 0; F2:= 0;

for I:= 1 to N do

Begin R2:= Y1+ X1*F1- X2*F2;

F2:= Y2+ X1*F2+ X2*F1; F1:=R2;

R1:= A[I]+ X1*Y1- X2*Y2;

Y2:= X1*Y2+ X2*Y1; Y1:=R1;

end;

R:= F1*F1+ F2*F2;

Q:= (Y1*F1+ Y2*F2)/R;

F2:= (Y2*F1- Y1*F2)/R; F1:=Q;

end;

procedure NewtonC;

Const E=1E-6;

Begin repeat PolinC;

X1:= X1-F1;

X2:= X2-F2;

until sqrt(F1*F1+F2*F2)<E

end;

Идентификаторы F1 и F2 использовали дважды. Значения этих параметров процедур передаются в процедуру Ньютона, которая запишется так:

Procedure Newton;

Const e = 1e-6;

Begin

Repeat polinc;

X1:=x1-f1; x2:=x2-f2;

Until sqrt(f1*f1+f2*f2)<e;

End:

Поскольку комплексные корни всегда сопряженные, то определенный пары корней требуют понижения порядка исходного уравнения (1) на два. Для сопряженных корней х=х1jх2 получим некоторое уравнение

Х² + рХ + q = 0,

где p = - 2Х, q = Х₁²+Х₂²

Поэтому исходное уравнение можно записать в виде:

Y(X) = (X² + pX + q)(b_n-2 + b_n-3X+…+b₁X^n-3 + b₀X^n-2), (13)

если X=X₁  jX₂ – корни исходного полинома Y(X).

Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях Х у левого и правого полиномов получим:

b₀ = a₀,

b₁ = a₁ - pb₀

b₂ = a₂ - pb₁ - qb₀

……………….

b_n-2 = a_n-2 – pbn-3-qb_n-4

Коэффициенты определяются рекурсивно. Запишем полученный алгоритм в виде процедуры:

Procedure Ponpor2;

Var p,q:real;

Var I: integer;

Type t=array[0..10]of real;

Var B:t;

BEGIN

B[0]:=A[0]; p:= - 2*X1; q:=X1*X2+X2*X2;

B[1]:= A[1] - p*B[0];

For I:=2 to N-2 do

B[I]:=A[I] – p*B[I-1] – q + b[I-2];

END;

Таким образом, мы имеем в распоряжении алгоритм (процедуры), которые позволяют решить характеристическое уравнение. Сходимость метода достаточно хороша. Зависит она от выбора величины начальных приближений для искомого корня. Точность определения корней может быть задана с точностью  в абсолютных величинах  = 10^-6 (см. процедуру NewtonR), а также в относительных величинах. В последнем случаи необходимо F поделить на Х (abs(F/x<e)).

Все сказанное применимо не только к алгебраическому уравнению (4), но и к любому нелинейному уравнению f(x) = 0. В задачах динамики при рассмотрении реальных нелинейных математических моделей ОУ и СУ такие задачи встречаются достаточно часто. Особенно это требуется для решения систем нелинейных уравнений:

X = f(X), где (14)

Чтобы выполнить интегрирование системы нелинейных уравнений (14), необходимо знать нелинейные уравнения т.е. при t = 0, Х = Х₀. Если значения Х₀ соответствуют установившемуся режиму работы, то X = f(X) = 0. Поэтому и требуется решить систему уравнений f(X) = 0.

К решению систем нелинейных алгебраических уравнений мы вернемся позже, а сейчас перепишем ряд наиболее распространенных методов решения нелинейных уравнений:

• Метод хорд.

• Метод секущих (Kwdriter).

• Метод дихотомии (Dihot).

• Метод Лагерра.

• Метод простых интерполяцией (Iter).

Для решения алгебраических уравнений существуют методы:

• Мюллера (если при близких к друг к другу и комплексных корнях).

• Берстоу ( сходимость лучше, чем в методе Ньютона).

• Бернулли (дает приближения сразу по всем корням).

• Лобачевского (сначала определяет действительные и чисто мнимые корни).

• Матричные методы.

Существуют оценки сходимости методов и их точности, но в основном применительно к одному уравнению. Например, доказать что, точность определения корней характеристического уравнения будет выше, если корень определяется с участием всех коэффициентов характеристического уравнения, а не для управления по техническим системам.

Рассмотрим в заключении метод простых итераций. Он применим, если уравнение f(X) = 0 можно записать в следующем виде :

X = f₁(X) (15)

Алгоритм метода чрезвычайно прост:

• Задаем начальное приближение X=X₀

• Производим расчет f₁(X)

• Определяем новое приближение X₁ = f₁(X₀)

Далее процесс итераций продолжается до тех пор пока значения X_i+1 и X_i не сойдутся с заданной точностью . Очень наглядна графическая иллюстрация алгоритма:

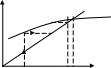
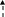
y y=x y

y=f₁(x) y=x

x₀ x₁ x₂ x^* X x^* x₀ x₁ X

рис.2 рис.3

х^* - искомый корень.

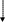
Н а рис. 2, 4 процесс итераций сходится, а на 3, 5 – расходится. Y y=f₁(x)

y y=x y=x y=f₁(x) x₀ x^* X x₀ x^* X

рис.4 рис.5

По этому легко установить критерий сходимости метода: процесс итераций сходится, если производная f₁’(x) по модулю меньше 1.

Решение систем линейных алгебраических уравнений.

Наиболее компактная форма записи :

Ах = В, (16)

x₁

x₂

где x = • , а А и В – матрицы.

•

•

x_n

Система уравнений (16) :

• имеет решение и оно единственное,

• не имеет решений ,

• имеет бесконечное множество решений.

Поэтому система уравнений называется вырожденной, если решений нет или их бесконечное множество. Существуют плохо обусловленные системы, когда решение не достоверно. Например,

5х +7у =12

7х+10у=17

решение х=у=1. Возьмем у=0, а х=4,415, тогда получим совпадение по первым частям с точностью

12,075 =12 \ 0,075\ 5 + 7 =12

16,905 = 17 \0,095\ 7 + 10=17

Очень наглядна геометрическая иллюстрация решения системы двух уравнений:

2х+у=4,

х -у=-1: точка пересечения двух прямых (х=1,у=2).

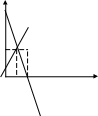
4 у

3 х-у=-1

2

1 2х+у=4

0 1 2 3 4 Х

В пространстве трех переменных точка пересечения трех плоскостей и далее – гиперплоскости. На плоскости – иллюстрация отсутствия решений – параллельность прямых; бесконечное множество решений – совпадение прямых. Последнее обстоятельство практически очень полезно, так как указывает на линейную зависимость строк в матрице А точно также на отсутствии решения указывает равенство детерминанта det A =0.

Существуют прямые и итерационные методы численного решения системы линейных уравнений.

Формально прямые методы содержат лишь ошибки округления, а на итерационные – ошибки ограничения, но при итерационном методе ошибки округления не накапливаются. При практических расчетах не эти обстоятельства будут решающими.

Метод Гаусса.

Рассмотрим его применительно к системе трех уравнений:

a₁₁x₁+a₁₂x₂+a₁₃x₃=b₁,

a₂₁x₁+a₂₂x₂+a₂₃x₃=b_2, (17)

a₃₁x₁+a₃₂x₂+a₃₃x₃=b₃, где

a₁₁ a₁₂ a₁₃ b₁

A = a₂₁ a₂₂ a₂₃ В = b₂ , поэтому Ах =В.

а₃₁ a₃₂ a₃₃ b₃

Введем множитель m₂=a₂₁/a₁₁ и умножим на него первое уравнение системы, затем вычтем его из –2-го уравнения:

(a₂₁-m₂a₁₁)x₁+(a₂₂-m₂a₁₂)x₂+(a₂₈-m₂a₁₂)x₃=b₂-m₂b₁, a₂₁-m₂a₁₁=0

Второе уравнение системы приобретает вид a’₂₂x₂+a’₂₃x₃=b’₂, где новые обозначения очевидны. Введем множитель для третьего уравнения m₃=a₃₁/a₁₁,вновь умножаем на него первое уравнение, вычтем его из третьего, получим

(a₃₁-m₃a₁₁)x₁+(a₃₂-m₂a₁₂)x₂+(a₂₂-m₃a₁₃)x₃+b₃-m₃b₄

где вновь a₃₁-m₃a₁₁=0 и получено 3-е уравнение системы:

a₁₁x₁+a₁₂x₂+a₁₃x₃=b₁

a’₂₂x₂+a’₂₃x₃=b’₂ (18)

a’₃₂x₂+a’₂₃x₃=b’₃

Аналогичным образом введем новый множитель m”₃=a’₃₂/a’₂₂ и умножим на него второе уравнение системы (18) , и вновь вычтем из третьего:

(a’₃₂-m’₃a’₂₂)x₂+(a’₃₃-m’₃a’₂₃)x₂=b’₃-m’₃b’₂

Получим систему уравнений в виде:

a₁₂x₁+a₁₂x₂+a₁₂x₃=b₁

a’₂₂x₂+a’₂₃x₃=b’₂ (15)

a”₃₃x₃=b”₃

Указанным приемом удалось исключить x, из второго и третьего уравнения и х₂- из третьего. Такой метод имеет смысл лишь в случае, если

Поскольку систему уравнений (17) свели к к треугольному виду (19), то ее легко решить обратной подстановкой:

Равенство а₁₁=0 или a’₂₂=0 указывает на вырожденность системы.Таким образом алгаритм метода Гаусса состоит из двух частей:

• приведение системы к треугольному виду

• решение системы обратной подстановкой

Указанный алгоритм реализован в следующей процедуре. Различие заключается в том, что оставшиеся значения всегда будут переставляться так, чтобы чтобы наибольший по модулю коэфициент при х_к падал на главную диоганаль.Указанный прием существенно уменьшает ошибку округления.

Proceadure GAUSS;

Var I_{,J,K,L,Kl,NI:} integer;

Var S,R: teal;

Begin NI=N+I; for k:=1 to N do begin

Kl:=k=1; s:=a [k₁k]; j:=k;

For I:=kl to N do begin R:= A[I₁K];

If abs (R) > abs (S) then begin S:=R ;J:= I: end;

End;

If s:=0₁0 then exit ; if J<>K then

For I:=K to N1 do

Begin R:=A[K₁I] ; A[K₁I]:=A[j₁i] ; A[j₁i]:=R ; end

For j:= kl to N1 do A[k₁j]:=A[k₁j]/S ;

For I:=kl to n do begin R:= A[i₁k];

For j:=kl to N1 do A[I₁J]:=A[I₁J] A[K₁J]*R; end;end;

{обратная подстановка}

if S<>0,0 then

for I:=N downto 1 do

begin S:= A[I₁N₁] ; for j:=j+1 to N do

S:=S-A[I₁jJ*X[J];

X[I]:=S

End; end;

Методика А должна быть описана и оформлена по заданным коэффициентам с учетом столбца первых частей. Число уравнений N-заданно. S- описано в основной программе. Там же описан Х- вектор результатов (решение). Решение отсутствует если S=0.

Метод итерации Гаусса-Зейделя.

Рассмотрим метод на примере трех линейных уравнений (17)

Преобразуем в систему к виду:

X₁= 1/a₁₁ (b₁-a₁x₂-a₁₃x₃)

X₂=1/a₂₂ (b₂-a₂₁x₁-a₂₃x₃)

X₃=1/a₃₃ (b₃-a₃₁x₁-a₃₂x₂)

Если задать начальные приближенные для x⁰_1,x⁰₂,x⁰₃, то получим из первого уравнения системы (17)

X’₁=1/ a₁₁ (b₁-a₁₂x⁰₂-a₁₃x⁰₃), использовав X’₁,получим из 2-го уравнения системы:

X’₂=1/ a₂₂ (b₂-a₂₁x’₁-a₂₃x⁰₃).И, аналогичным образом, для 3-го уравнения получим: X’₃=1/ a₃₃ (b₃-a₃₁x’₁-a₃₂x’₂). И далее процесс итераций следует повторять до схождения полученных значений x_kⁱ⁺¹ - x_kⁱ <ع.

Строго говоря , это не метод простых итераций, поскольку X’₂ использует новое значение X’₁ , а X’₃ – значения X’₁ и X’₂ . Поэтому, если поставить вместо «0» индекс i, а вместо «1» – «i+1» получим общий алгоритм метода:

X₁ⁱ⁺¹=1/ a₁₁ (b₁-a₁₂xⁱ₂-a₁₃xⁱ₃),

X₂ⁱ⁺¹=1/ a₂₂ (b₂-a₂₁xⁱ⁺¹₁-a₂₃xⁱ⁺¹₃),

X₃ⁱ⁺¹=1/ a₃₃ (b₃-a₃₁xⁱ⁺¹₁-a₃₁xⁱ⁺¹₂).

Достаточные условия сходимости метода:

a_ii ≥ a_i1 +… + a_i,i-1 + a_i,i+1 + … + a_in

для всех i или по крайней мере для одного i

a_ii > a_i1 +… + a_i,i-1 + a_i,i+1 + … + a_in .

Если итерационные методы сходятся , то они предпочтительнее , так как время вычисления у них на одну итерацию пропорционально n² , а у метода исключения n³ . При числе итераций меньше n получается выигрыш по времени. Кроме того, ошибки округления при итерационном методе меньше.

Особенно наглядно геометрическое представление итерационного методе для системы уравнений :

Y 2x+y=2,

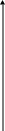x-2y=-2.

Условия сходимости:

a₁₁ > a₁₂

a₂₂ > a₂₁

2 x-2y=-2

-2 -1 0 1 2 X

2x+y=2

рис.7

Переставим уравнения , т.е. начнем со второго уравнения. Очевидно , что процесс итерации в этом случае расходится.

Представим алгоритм метода Зейделя в виде процедуры.

Procedure SELD;

var I, J:integer; var E, S: real;

begin

E:=1E-7; M:=10;

For k:=1 to M do begin L:=k;

For I:=1 to N do begin S:=A[I,N+1];

For J:=1 to N do

S:=S-A[I,J]*X[J];

S:=S/A[I,I]; X[I]:=X[I]+S;

If cls(S)>E then L:=0; end;

If L<>0 then exit;

End; end;

Матрицы коэффициентов А и В (Ах=В) заданны и описаны в основной программе. Число уравнений N, допустимое число итераций М заданно в основной программе. Полученное число итераций М является выходным параметром программы и его следует описать в основной программе и задать k=0 .

Итерационные методы особо привлекательны для разряженных матриц .

Рассмотрим два важных метода, которые используют алгоритмы решения систем линейных уравнений:

1. Метод Ньютона (обобщенный) для решения систем нелинейных уравнений: f(x)=0,где (*)

x и f вектора.

Формируем матрицу Якоби: f(x)=f(x_i⁰) +∂f∆x_i/∂x_i

∂ f₁/∂x₁ ∂f₁/∂x₂ … ∂f₁/∂x_n Чтобы избежать аналитического

∂f₂/∂x₁ ∂f₂/∂x₂ … ∂f₂/∂x_n нахождения производных, используем

… … … … матрицу Якоби для приближенных

∂f_n/∂x₁ ∂f_n/∂x₂ … ∂f_n/∂x_n (конечно - разностных) соотношений:

∂f_i/∂x_i≡ f_i(x_i+∆x_i)- f_i(x_i)/ ∆x_i

Замена левой части уравнения f’(x_i⁰) ∆x_i = - f(x_i⁰);

Систему линейных уравнений формируем по правилу: f’(x_i) (x_i+1 - x_i )= - f(x_i);

∆x_i

Интерполяция.

А. Известны значения таблично заданной функции. Необходимо определить значение

ф-ции между “узлами таблицы”. Обычно таблицы бывают двух- и трёх- мерными. Перед

вычислением стоит четыре вопроса: