1.3. Схема Горнера и метод Ньютона

Если известны корни характеристического уравнения n порядка (1.10), то его можно представить в виде:

, (1.11)

где x₀ ,x₁ ,, x_n – корни уравнения. Исходный полином (1.10) разложили на множители. Соотношение между коэффициентами и корнями уравнения можно получить перемножив левую часть уравнения (1.11). Этот алгоритм существует.

Аналитическое решение известно лишь для уравнений до 4-го порядка. Численные методы позволяют рассчитать корни характеристического уравнения высокого порядка. Знание корней необходимо для получения аналитического решения обыкновенных дифференциальных уравнений и для анализа устойчивости систем.

Критерии устойчивости разрабатывались по той причине, что они позволяли судить об устойчивости системы, не вычисляя корней. А вычислить корни без ЭВМ было весьма трудно.

Рассмотрим наиболее распространенные методы численного решения алгебраических уравнений. Для этого введем в рассмотрение схему Горнера, которая позволяет более рационально рассчитывать полиномы вида (1.10):

.

Запишем правую часть функции f(x) в виде:

(1.11)

Если раскрыть скобки и приравнять коэффициенты при одинаковых степенях x в формулах (1.10) и (1.11), то получим соотношение между коэффициентами a и b:

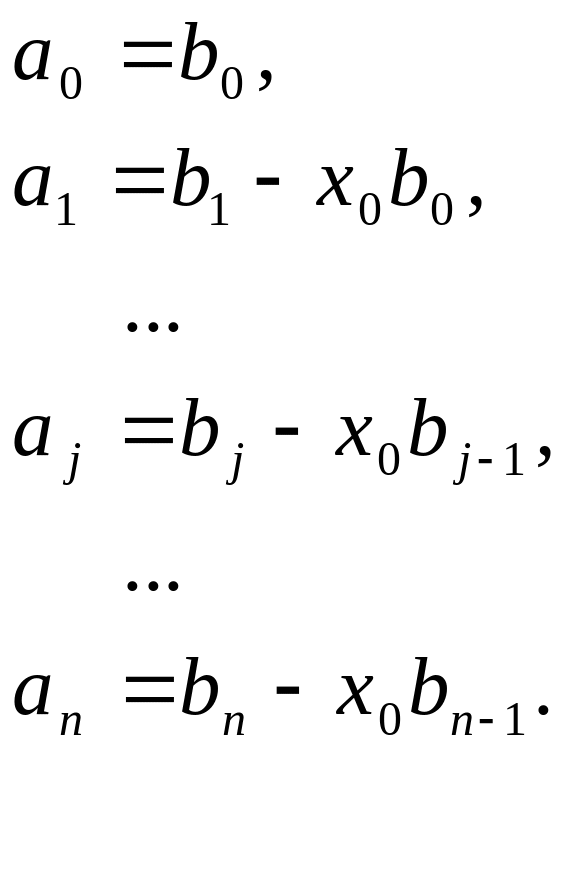(1.12)

коэффициенты a известны, поэтому перепишем соотношения (1.12) в виде:

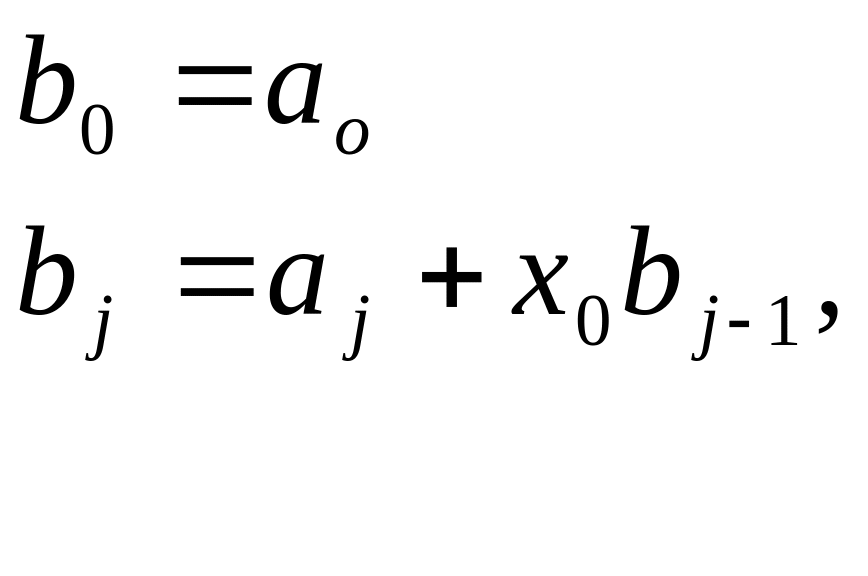(1.13)

где j=1,2,…,n. Если x₀ корень уравнения, то мы получили соотношение (1.13) для коэффициентов уравнения порядка. Используем его для записи уравнения 5-го порядка: 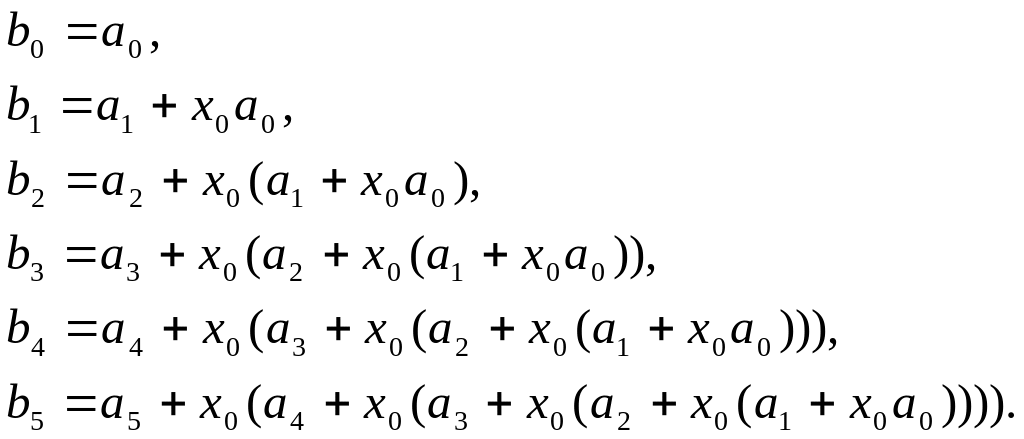(1.14)

Получен алгоритм расчета полинома по схеме Горнера - последняя строка (1.14). Если x₀ корень уравнения (1.10), то коэффициент b_n = 0.

Поделим обе части (1.11) на x-x₀ :

Если x₀ корень уравнения (1.10), то деление полиномов происходит без остатка (теорема Безу). Остаток (для любого x₀) определяется по схеме Горнера (последняя строка (1.14)). Для уравнения n порядка вычисление по схеме Горнера выполняются по алгоритму:

(1.15)

Обозначим f(x)=y и запишем каждую пару слагаемых, начиная с последней, следующим образом:

присвоим y = a₀ и в цикле считаем

y=a(k)+y*x, где k=1,2,3,…,n. (1.16)

При вычислении по схеме Горнера требуется 2n арифметических действий, а по формуле (1.10) .

Реализуем алгоритм на МATLAB.

function [f]=gornR

a = [1 3 3 1]; n = 3; y = a(1); x = -1;

for k=2:n+1

y=a(k)+y*x;

end

Конечно, алгоритм справедлив лишь для вещественных корней. Его можно применять для алгебраического уравнения, если n нечетное. Если корень определен, то далее используется алгоритм понижения порядка (1.13):

function [a,b]=ponporR

n = 4; a = [1 4 6 4 1]; x = -1;

b(1) = a(1);

for k=1:n-1

b(k+1) = a(k+1) + x*b(k);

end

n=n-1;

for k=1:n+1

a(k)=b(k);

end

Т.е. новый вектор a получен для характеристического уравнения степени .

Определить вещественный корень можно методом Ньютона. Алгоритм метода легко получить из графика

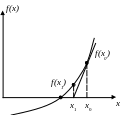
рис. 1.1

Задаем начальное приближение x₀ , определяем f(x₀) и производную . Пересечение касательной с осью абсцисс позволяет определить новое приближение x₁.

Запишем приближенное значение производной в точке x₀

, откуда