Метод Рунге-Кутты для решения обыкновенных дифференциальных уравнений.
На
практике наиболее часто используют
метод Рунге—Кутты четвертого порядка.
Пример
3.
Решить
задачу Коши для ДУ
y(x)
= x
+ cos
— на
отрезке [1,7; 2,7] при заданном НУ: y(1,7)
=5 ,3 и шаге интегрирования h
=
0,1 методом Рунге-Кутты четвертого порядка
с шагом h
и
2h.
Решение.
1.
Вводим
данные задачи:
f(x,y)
:=
x
+cos
а
:= 1.7
b
:= 2.7
h:=
0.1
п:
= 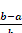
у0
:= 52
i
:=
0..п
Составим
функцию, возвращающую решение ДУ первого
порядка методом Рунге—Кутты (Рис.
21).
Здесь: fn
—
заданная функция; a,
b
—
концы отрезка; h
—
шаг; у0
—
начальное значение функции.
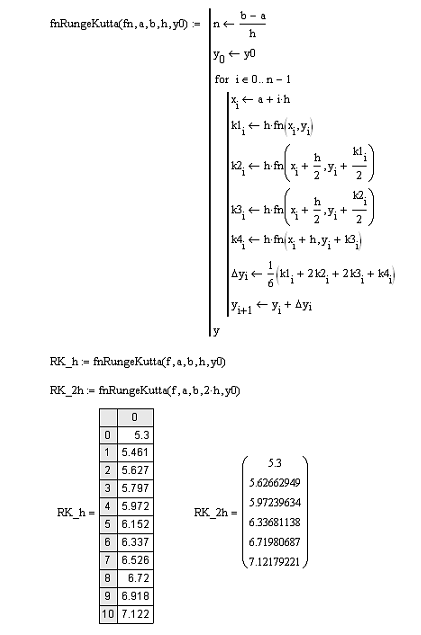
Рис.
21. Листинг функции, возвращающей численное
решение ДУ методом Рунге-Кутты.
Ответ:
Решением
ДУ
y(x)
= x
+ cos
на
отрезке [1,7; 2,7] с НУ y(1,7)
=5,3 методом Рунге-Кутты четвертого
порядка с шагом h
и
2h
будет
таблица значений RK_h
и
RK_2h
(Рис.
21).


