2.3. Метод Эйлера и его модификации для решения обыкновенных дифференциальных уравнений.

В основе метода Эйлера лежит идея графического построения решения ДУ (Рис. 15).

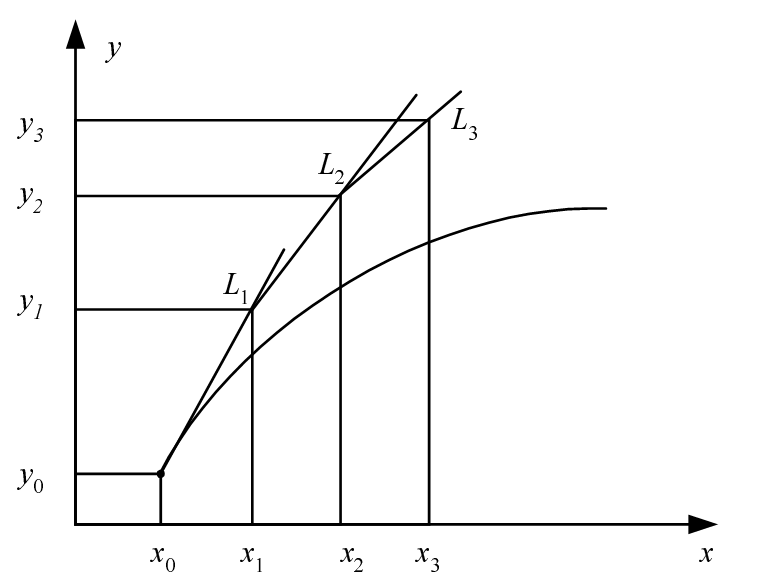
Рис. 15. К объяснению метода Эйлера

Пусть дано дифференциальное уравнение:

с начальным условием у₀ = у(х₀). Выбрав дос­таточно малый шаг h, построим, начиная с точки х₀, систему равноотстоя­щих точек x_i = x₀ + ih (i = 0,1, 2,...). Вместо искомой интегральной кривой на отрезке [x_0,x_i] рассмотрим отрезок касательной к ней в точке M₀(x₀,y₀), уравнение которой:

у= у₀ + f(x₀, y₀) • (х - х₀).

При x=x₁ из уравнения касательной получаем у₁ = у₀ + h f(х₀, у₀). Следова­тельно, приращение функции на первом шаге равно ∆у₀ = h f(х₀, y₀). Проведя аналогично касательную к интегральной кривой в точке (x₁, y₁), получим:

y = y₁+f(x₁,y₁)*(x-x₁),

что при х = х₂ дает у₂ =у₁ + h f (x₁,y₁), т. е. у₂ получается из у₁ добавлени­ем приращения ∆y₁₌ hf(x₁,y₁).

Таким образом, вычисление таблицы значений функции, являющейся реше­нием ДУ, состоит в последовательном применении пары формул:

∆y_k=hf(x_k,y_k), y_к+1=y_к+∆y_к

Метод Эйлера, как видно из рисунка, имеет погрешность. Известны различные уточнения метода Эйлера. Модификации данных мето­дов направлены на уточнение направления перехода из точки (х_i,у_i) в точку (x_i+1,y_i+1). Например, в методе Эйлера—Коши (усовершенствованный метод) используют следующий по­рядок вычислений:

y^*_i+1 =y_i+hf(x_i,y_i), y_i+1=y_i+ h ( f (x_i,y_i) + f(x_i+1,y^*_i+1) ) /2,

Геометрически это означает, что определяется направление интегральной кривой в исходной точке (х_i,у_i,) и во вспомогательной точке (x_i+1,y^*_i+1), а в качестве окончательного берется среднее значение этих направлений.

Пример 1. Решение дифференциального уравнения методом Эйлера.

Решить задачу Коши для ДУ y(x) = x + cos — на отрезке [1,7; 2,7] при заданном НУ: y(1,7) =5,3 и шаге интегрирования h = 0,1 методом Эйлера с шагом h и h/2.

Решение.

Ход решения задачи по методу Эйлера приведен на Рис. 16.

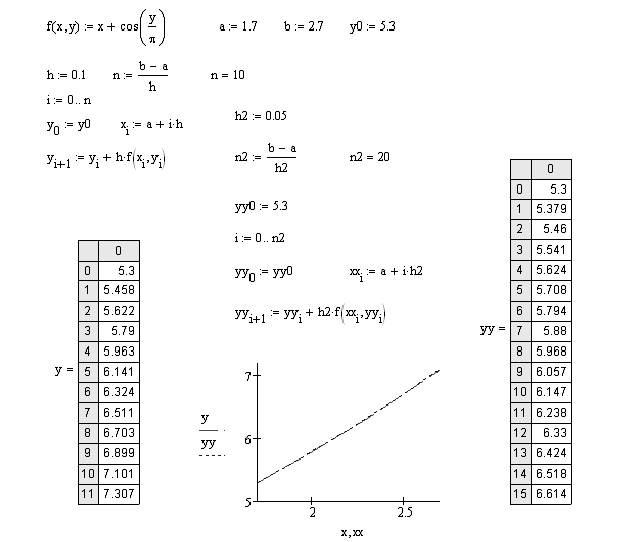
Рис. 16. Фрагмент программы с решением уравнения методом Эйлера с шагом с шагом h и h/2.

1. Составим программу, реализующую метод Эйлера (Рис. 17).

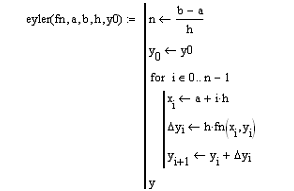
Рис. 17. Листинг программы, реализующий метод Эйлера.

2. Получим решение ДУ методом Эйлера с двумя шагами h и h/2(Рис. 18).

Рис. 18. Нахождение численного решения ДУ методом Эйлера.

3. Ответ: Решением ДУ y(x) = x + cos на отрезке [1,7; 2,7] с НУ y(1,7) =5,3 методом Эйлера с шагом h и h/2 будет таблица значений ES_h и ES_h2 (Рис. 21).

Пример 2. Решение дифференциальное уравнение усовершенствованным методом Эйлера.

1. Задание функции, реализующей метод Эйлера—Коши (Рис. 19). Аргу­менты функции: у0 - значение решения в точке х0 ; х0, xl — левый и правый концы интервала вычисления численного решения; N — число сетки, на которой ищется решение ДУ; f — имя функции, стоящей в правой части ДУ. Функция возвращает таблицу, состоящую из двух столбцов, первый столбец— значения аргумента, второй столбец— зна­чения решения ДУ.

Рис. 19. Функция, реализующая метод Эйлера—Коши для ДУ первого порядка.

2. Нахождение численного решения ДУ на интервале [0,5]:

А1:=Euler1(x0, y0, x1, N, f)

3. Визуализация численного решения (Рис. 20).

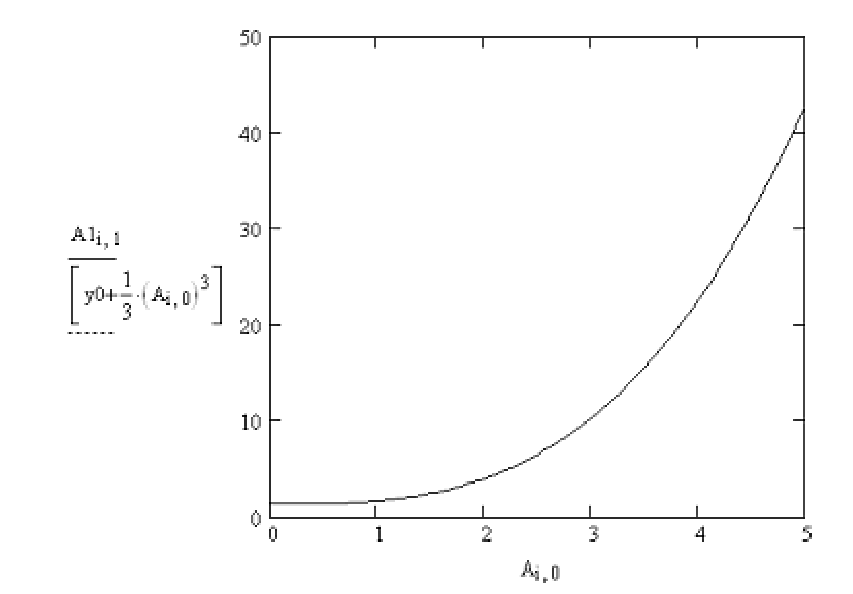
Рис. 20. Численное решение ДУ y^’=x² полученное методом Эйлера.