1. Линейная алгебра и аналитическая геометрия

1.Системы линейных уравнений

Рассмотрим систему m линейных уравнений с n переменными

Решением системы называется набор значений переменных (с₁, … , с_n), при подстановке которых в систему все уравнения обращаются в верные равенства.

Система называется несовместной, если она не имеет решений.

Решить систему – значит найти множество всех ее решений.

Две системы от одних и тех же переменных называются равносильными, если любое решение каждой из этих систем является решением другой.

Система называется однородной, если все ее свободные члены равны 0. Однородная система всегда совместна, так как имеет нулевое решение.

Для решения системы используется метод Гаусса, заключающийся в последовательном исключении переменных. Для удобства систему записываем в виде матрицы (то есть прямоугольной таблицы, заключенной в круглые скобки и заполненной числами), построенной из коэффициентов и свободных членов системы. При этом столбец свободных членов отделяется от остальных столбцов вертикальной чертой. Матрица имеет вид

Такая матрица называется расширенной матрицей системы, а матрица из одних коэффициентов, без столбца свободных членов – основной матрицей.

Над системой допускается производить следующие элементарные преобразования, которые приводят к равносильной системе:

1. умножение какого-либо уравнения на скаляр   0;

2. прибавление к уравнению другого уравнения, умноженного на скаляр ;

3. исключение из системы или добавление к ней уравнения с нулевыми коэффициентами и свободным членом.

Соответствующие преобразования производятся над строками матрицы системы. Преобразования приводят к эквивалентным матрицам, переходы обозначаются знаком эквивалентности ~.

Первый ненулевой коэффициент в каждой строке называем ведущим.

Цель преобразований – избавиться от переменной x₁ во всех уравнениях, кроме первого. Считаем, что в первой строке ведущий элемент - a₁₁. В противном случае поставим на первое место другую строку. Используем первую строку как опорную.

Чтобы избавиться от первого коэффициента a_i1 в i-ой строке, прибавляем к этой строке первую строку, умноженную на (–a_i1/a₁₁). Проделав это со всеми строками, начиная со второй, во всех этих строках на первом месте получим 0.

Возможно, что при этом станут нулевыми все элементы не только в первом столбце, но и в нескольких следующих (без первой строки). Если же какие-нибудь ненулевые элементы в получившейся матрице останутся, то повторяем указанные преобразования с матрицей, получающейся отбрасыванием первой строки и всех столбцов до первого ненулевого.

Проделав указанные преобразования, сколько возможно, получим матрицу в ступенчатом виде. Он характеризуется тем, что ведущий элемент в каждой строке, начиная со второй, расположен правее, чем в предыдущей.

Если в последней ненулевой строке ступенчатой матрицы слева от черты стоят нули, а справа ненулевой элемент, то соответствующая система решений не имеет, то есть является несовместной.

Если такой строки в ступенчатой матрице нет, то для удобства обведем ведущие элементы во всех строках в кружки. Переменные, которым соответствуют кружки, считаются базисными, остальные – свободными. Если свободных переменных нет, то система имеет единственное решение. Для его нахождения по строкам получившейся матрицы восстанавливаем уравнения, начиная с последней, и последовательно находим значения всех переменных.

Если в системе есть свободные переменные, то придаем им произвольные значения, считая параметрами. Базисные переменные выражаются через них в том же порядке, как в предыдущем случае. Система в этом случае является неопределенной, то есть имеет больше одного решения.

Если система однородная, то в матрице столбец свободных членов не нужен, так как в этом столбце все элементы нулевые, они останутся нулевыми при любых преобразованиях.

Пример 1.1.1. Решить систему

Решение. Строим матрицу системы и приводим ее к ступенчатому виду:

~ ~

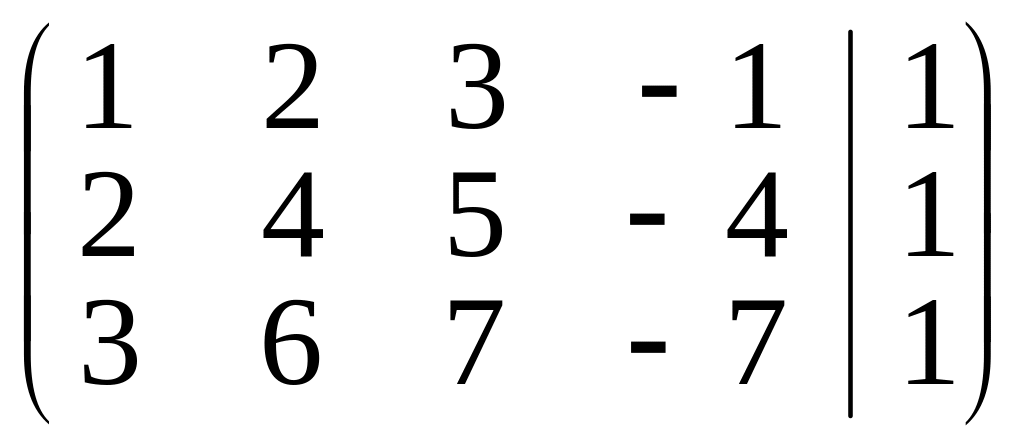Ко второй и третьей строкам первой матрицы прибавлялась первая строка, умноженная на –2 и –3 соответственно. К третьей строке второй матрицы прибавлялась вторая строка, умноженная на –2.

Базисными являются переменные x₁ и x₃, свободными x₂ и x₄. Полагаем x₂ = a, x₄ = b. Тогда из уравнения, соответствующего второй строке ступенчатой матрицы, получаем –x₃ – 2b = –1, и x₃ = –2b + 1. Подставляя в первое уравнение, получаем

x₁ + 2a + 3(– 2b + 1) – b = 1, x₁ = – 2a + 7b – 2.

Ответ: x₁ = – 2a + 7b – 2, x₂ = a, x₃ = – 2b + 1, x₄ = b, a, b ℝ.

У п р а ж н е н и е 1.1. Решите системы:

а)

б)

в)

г)