13

2. Кинематика cодержание теории

1. Кинематическое уравнение движения.

2. Скорость и ускорение – дифференциальные характеристики движения.

3. Средние скорость и ускорение.

4. Угловая скорость, угловое ускорение. Связь между угловыми и линейными величинами.

5. Кинематическое уравнение вращательного движения материальной точки.

6. Ускорение в плоском криволинейном движении. Нормальная и тангенциальная компоненты ускорения.

Основные формулы для решения задач

1. Положение материальной точки в пространстве задается радиус-вектором

,

где , , – единичные векторы направлений (орты); x, y, z – координаты точки.

2. Средние скорость и ускорение

Средний вектор скорости

где – перемещение материальной точки за интервал времени t; , , – средние значения проекций скорости на координатные оси; x=x(t)–х₀; y=y(t)–y₀; z=z(t)–z₀ – проекции перемещения материальной точки за интервал времени t; x₀, y₀, z₀ – начальное положение точки в пространстве.

Среднее значение скорости:

,

где s – пройденный путь за интервал времени t= t–t₀.

Средний вектор ускорения

где – приращение вектора скорости материальной точки за интервал времени t.

, , – средние значения проекций ускорения на координатные оси.

Среднее ускорение , где .

3. Мгновенные скорость и ускорение

Мгновенная скорость

где , , – единичные векторы (орты осей декартовой системы координат); ; ; – проекции скорости на координатные оси.

Модуль скорости

.

Мгновенное ускорение

Модуль ускорения

.

4. Кинематические уравнения движения

Кинематическое уравнение движения материальной точки в векторной форме

,

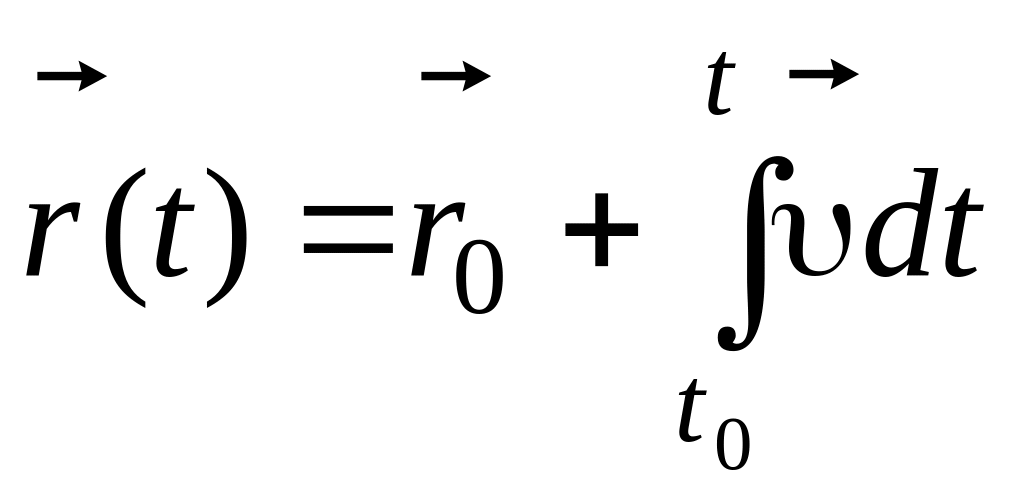где – радиус-вектор материальной точки в начальный момент времени t₀; – радиус-вектор в произвольный момент времени t; – закон изменения скорости точки со временем.

Векторное уравнение движения эквивалентно трем скалярным:

, , .

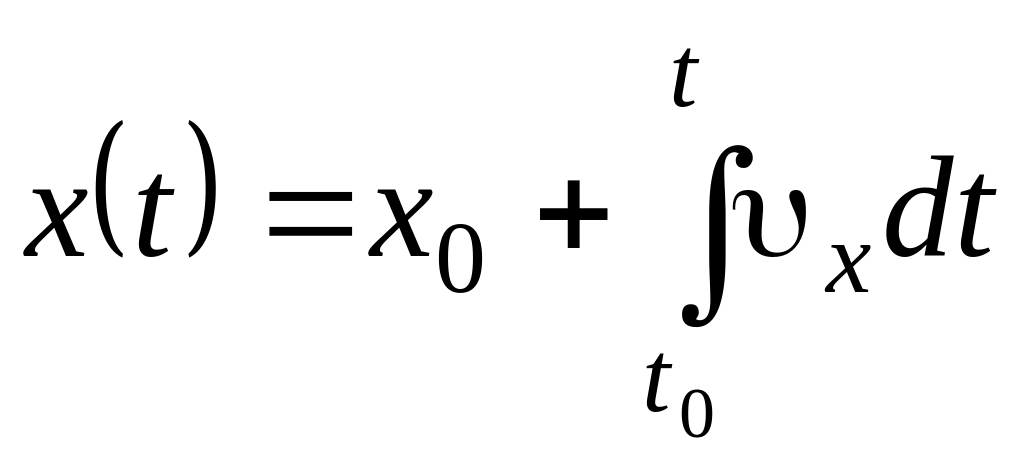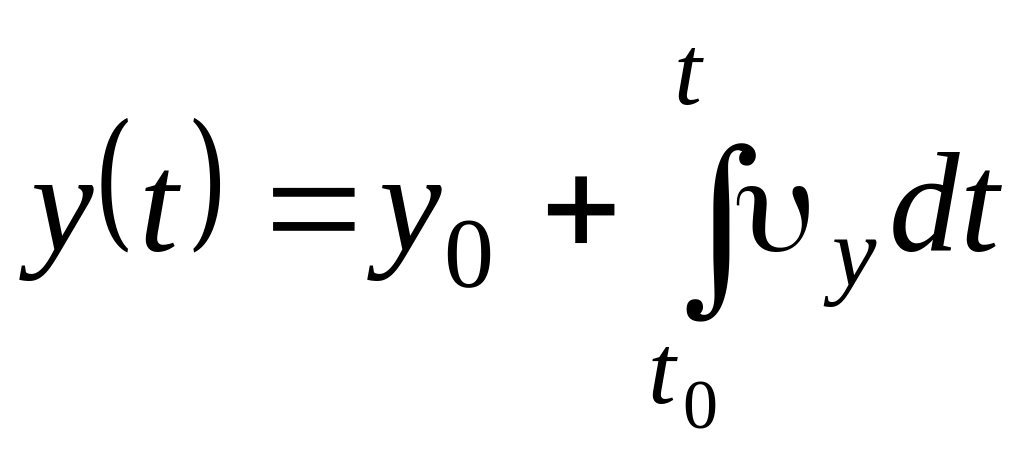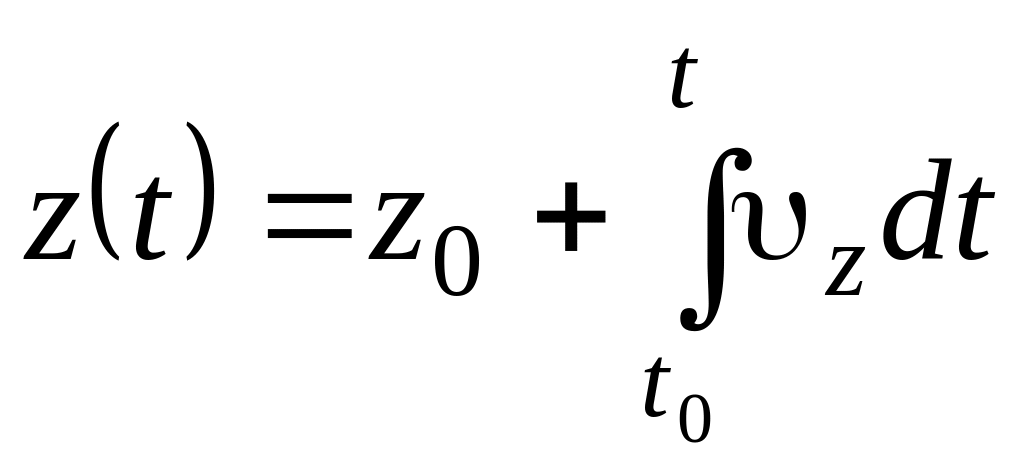Кинематическое уравнение равномерного прямолинейного движения материальной точки вдоль оси x

.

Кинематическое уравнение равнопеременного прямолинейного движения (a=const) вдоль оси x

.

Скорость точки при равнопеременном движении вдоль оси x

.

Связь скорости и ускорения

.

5. Средние угловая скорость и ускорение

Средний вектор угловой скорости

,

где – приращение угла поворота за интервал времени t.

Средний вектор углового ускорения

,

где – приращение угловой скорости за интервал времени t.

Средняя угловая скорость

,

где .

Среднее угловое ускорение

,

где .

6. Мгновенные угловая скорость и ускорение

Мгновенная угловая скорость

, ,

где _z – проекция угловой скорости на ось вращения.

Угловое ускорение

, ,

где _z – проекция углового ускорения на ось вращения.

Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с неподвижной в пространстве осью вращения.

Связь между линейными и угловыми величинами:

S=R; =R; a_=_zR; a_n= =²R,

где R – радиус окружности, по которой движется точка; S – длина дуги окружности;  – угол поворота;  – линейная скорость; _z – проекция углового ускорения на ось вращения;  – угловая скорость; a_ – тангенциальное ускорение; a_n – нормальное ускорение.

При постоянной угловой скорости =2/T, =2, где Т – период (время одного полного оборота);  – частота вращения (число оборотов, совершаемых движущейся точкой в единицу времени).