7.5. Неравенство Чебышева

Доказательство ряда теорем, входящих в закон больших чисел, опирается на одно простое неравенство.

Каково бы ни было положительное число  вероятность того, что случайная величина отклонится от своего ма­тематического ожидания не меньше, чем на , ограничена сверху величиной 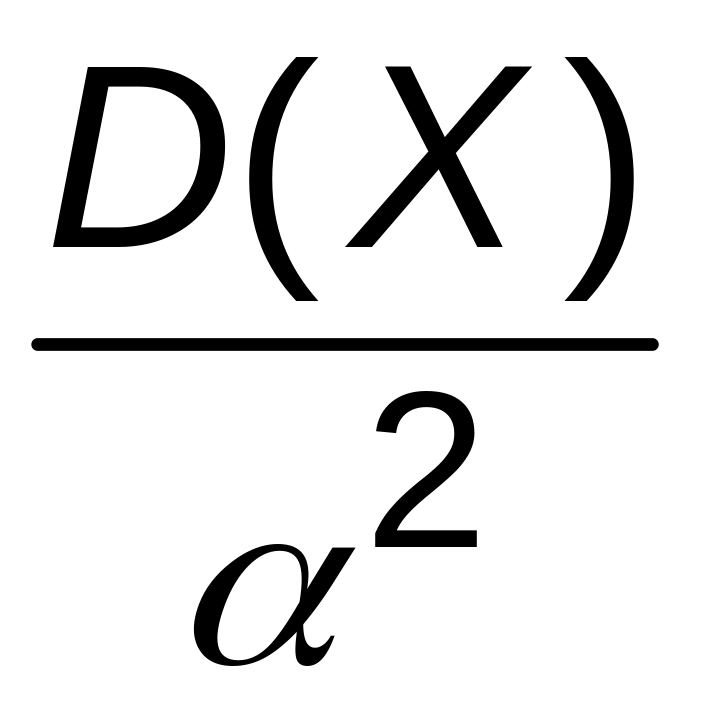, т.е.

.

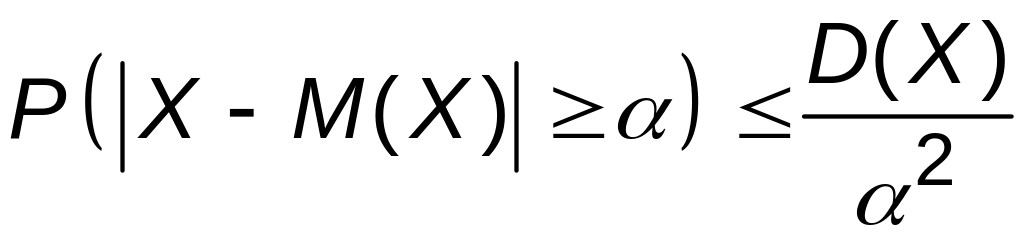Неравенство Чебышева можно записать в эквивалентной форме

,

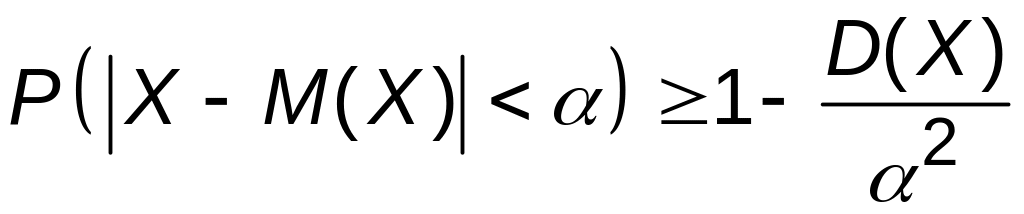так как события и противоположны.

Пример 7.5.

В осветительную сеть параллельно включено 25 ламп. Вероятность того, что за время Т лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время Т окажется а) меньше 6; б) не меньше 6.

Решение

По неравенству Чебышева вероятность отклонения значения случайной величины от своего математического ожидания оценивается так: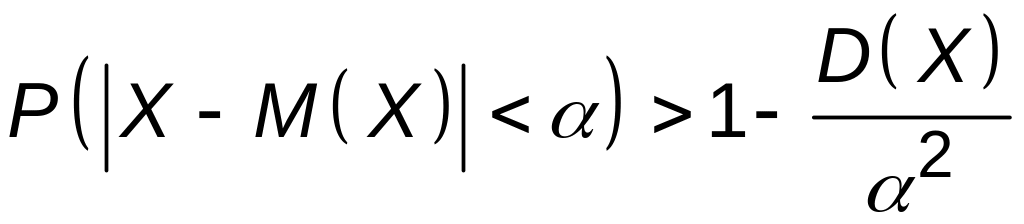 . Для повторных испытаний известно, что М(Х)=np=25·0,8=20, D(X)=npq=25·0,8·0,2=4, α=6.

Получим .

Из того, что , следует .

Определение. Говорят, что последовательность случайных величин сходится по вероятности к числу а, если при сколь угодно малом >о вероятность неравенства с увеличением n, неограниченно приближается к единице, т.е.

.

7.6. Теорема Чебышева

Теорема. Пусть наблюдается одна и та же случайная величина X с математическим ожиданием М(Х) и дисперсией . Обозначим через результат первого наблюдения, второго наблюдения и т.д.

При увеличении числа независимых опытов n среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию, т.е.

.

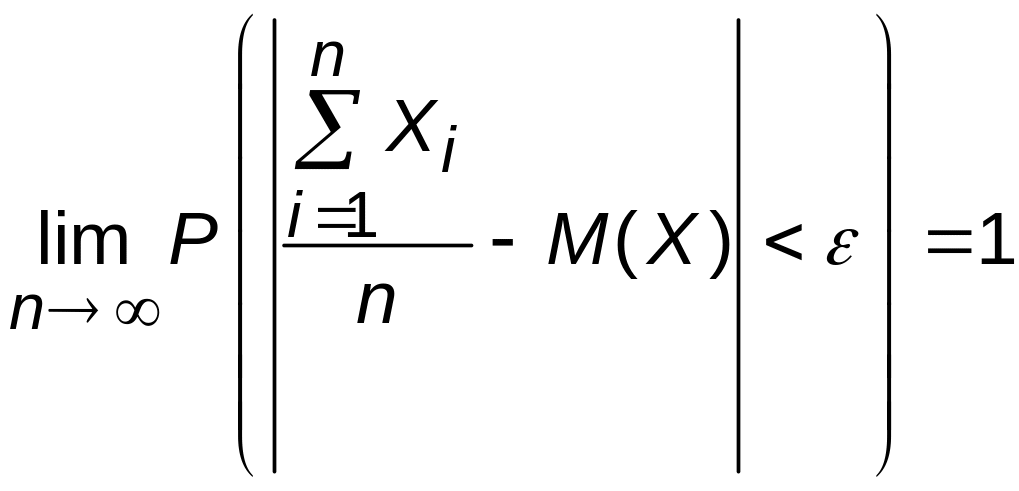Доказательство

Рассмотрим случайную величину

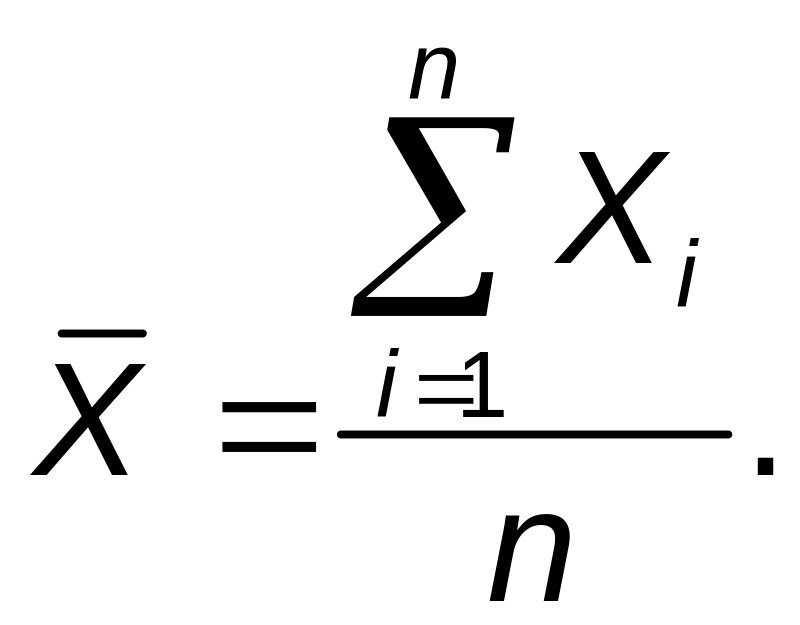
Случайные величины Х_i независимы и каждую из них можно рассматривать как отдельный экземпляр одной и той же случайной величины Х. Тогда

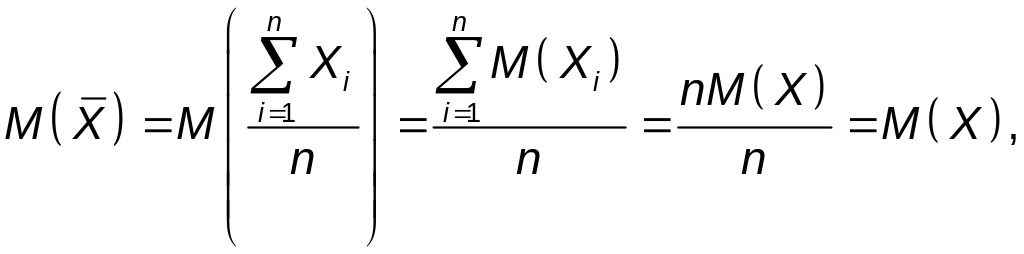
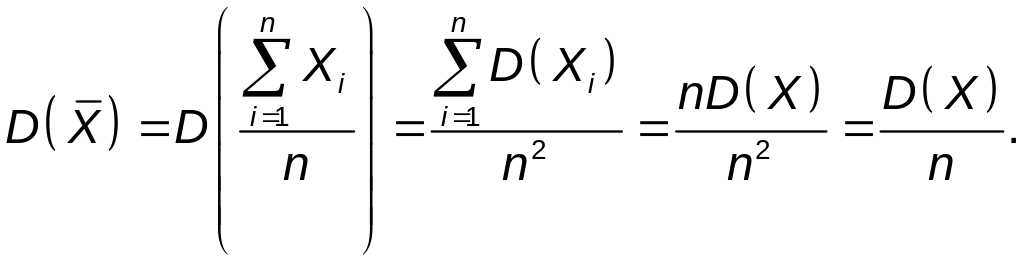
Из неравенства Чебышева для случайной величины следует, что

.

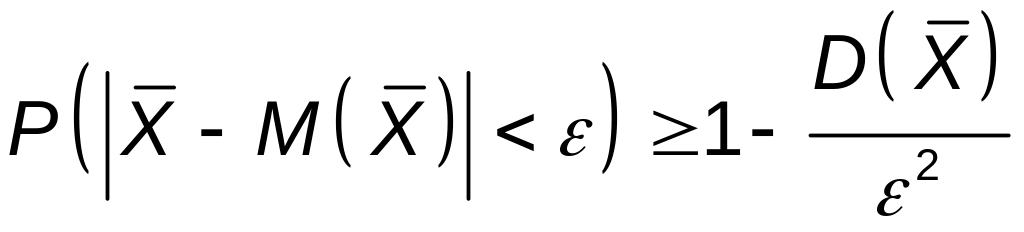Учитывая полученные выше результаты, имеем:

.

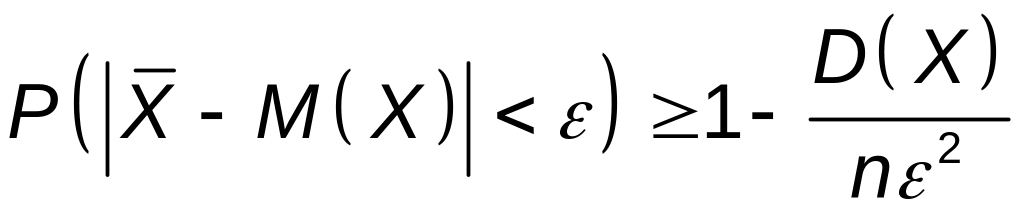Так как 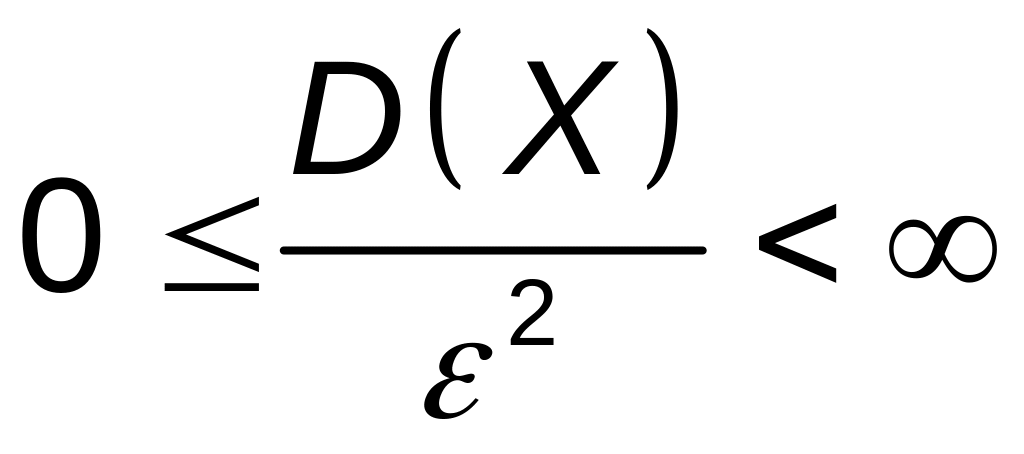, то .

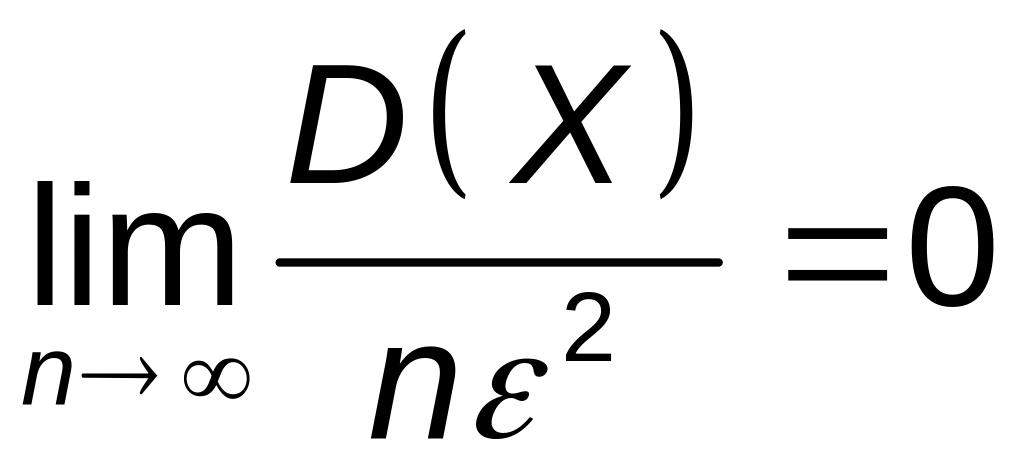Поэтому .

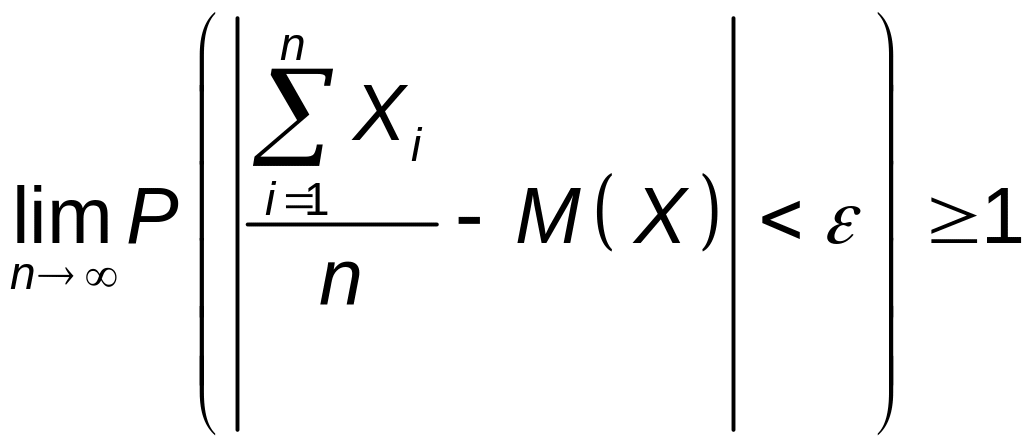Но вероятность не может быть больше единицы, поэтому в последнем соотношении неравенство можно заменить на равенство, что и является доказательством теоремы Чебышева.

Эта теорема обосновывает следующий способ определения математического ожидания случайной величины на основе опытных данных: нужно проделать достаточно много наблюдений случайной величины и вычислить среднее арифметическое наблюдаемых значений. Если число наблюдений велико, то почти достоверно, что, мало отличается от математического ожидания наблюдаемой величины и можно взять в качестве приближённого значения математического ожидания.

Обычно при измерении физических величин производят несколько измерений и в качестве значения измеряемой величины берут среднее арифметическое из результатов измерений. Обоснование такому способу действий даёт теорема Чебышева. Пусть мы измеряем некоторую физическую постоянную а. При измерении допускается некоторая ошибка X, и мы фактически получаем при измерении значение а + X. Если мы не делаем систематической ошибки, иначе говоря, если М(Х)=0, то М(а+Х)=М(а)+М(Х)=а. Значит, при достаточно большом числе измерений среднее арифметическое их результатов будет равно математическому ожиданию (по теореме Чебышева) и как угодно близко к а с вероятностью, близкой к единице. Таким образом, даже не точный прибор может обеспечить при указанном способе действий какую угодно точность.