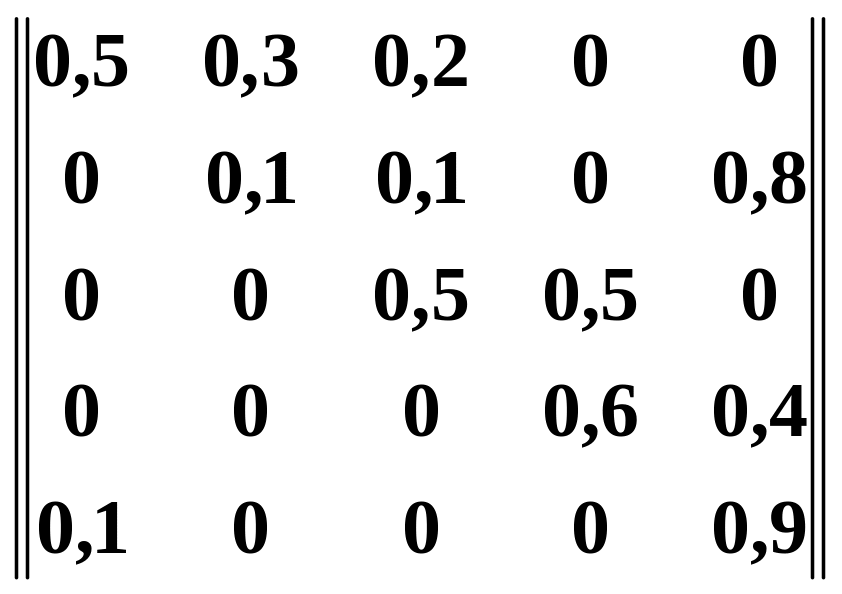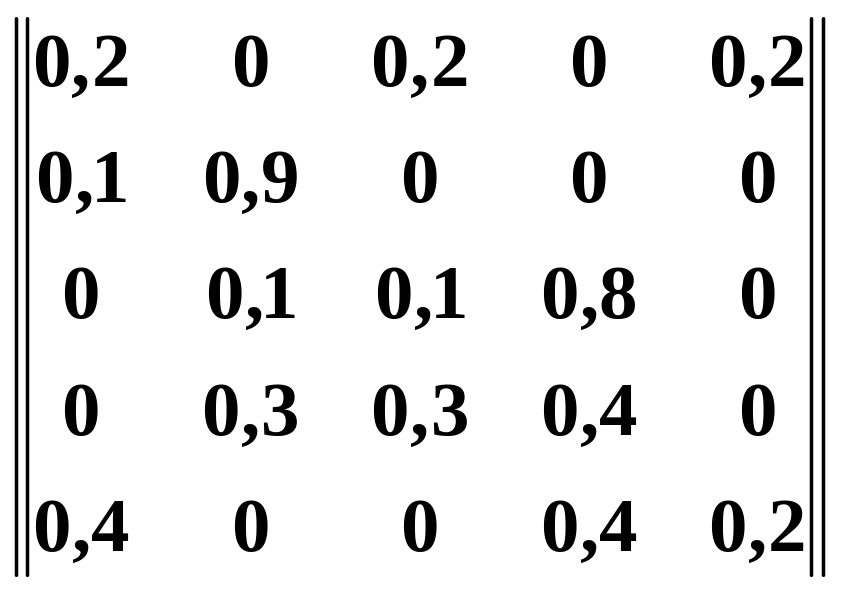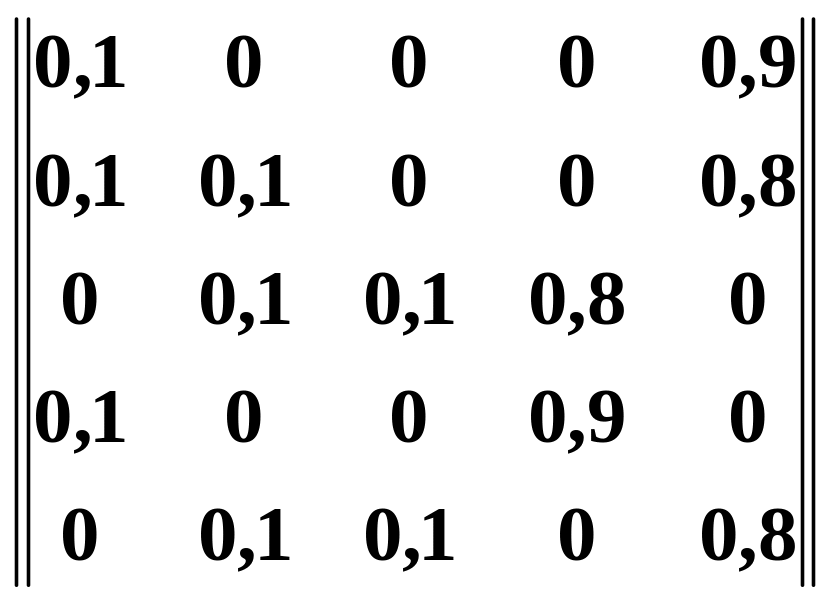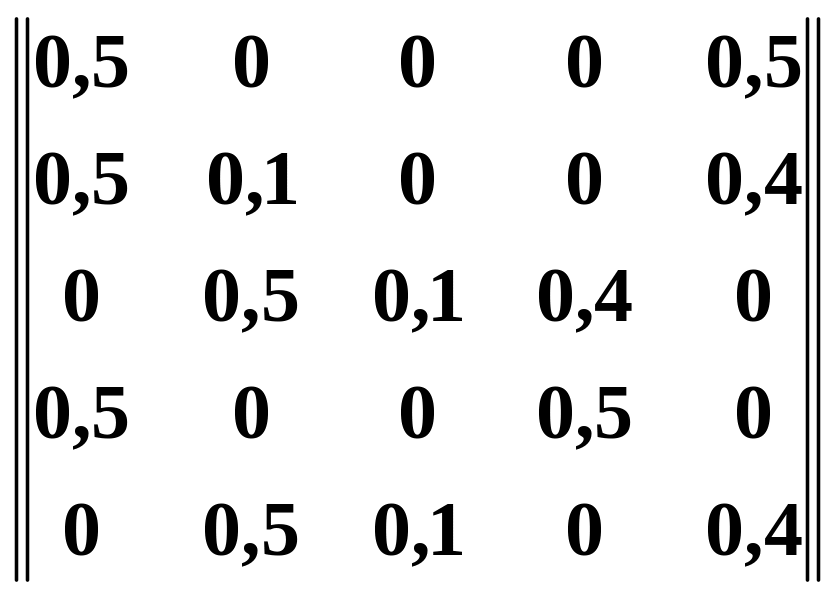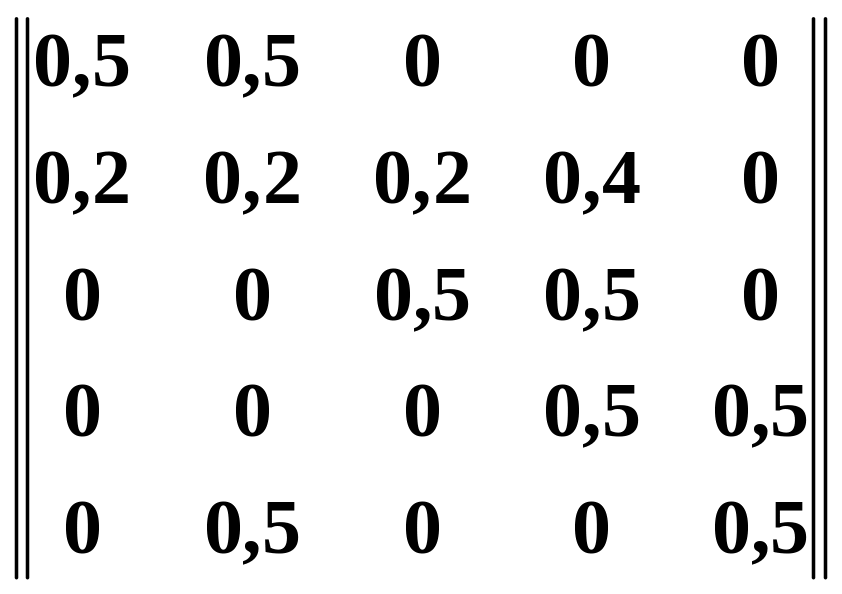- •Методичні вказівки та завдання
- •1 Лабораторна робота №1 Закони розподілу і основні характеристики випадкових величин……............................................................................5
- •1 Лабораторна робота № 1 закони розподілу і основні характеристики випадкових величин
- •1.1 Мета роботи
- •1.2 Означення випадкового процесу
- •1.3 Числові характеристики випадкового процесу
- •1.4 Деякі розподіли випадкових величин
- •1.4.1 Біноміальний розподіл
- •1.4.2 Розподіл Пуассона
- •1.4.3 Геометричний розподіл
- •1.7 Варіанти самостійного завдання №2
- •1.8 Приклади виконання завдання
- •1.8.1 Приклад завдання №1
- •1.8.2 Приклад завдання №2
- •2 Лабораторна робота № 2 марківські процеси з дискретними станами і з дискретним часом
- •2.1 Класифікація станів. Ймовірності станів
- •2.2 Марківські процеси з дискретними станами і з дискретним часом (ланцюги Маркова)
- •2.3 Марківські процеси з дискретними станами і з дискретним часом (стаціонарний режим)
- •2.4 Варіанти самостійного завдання №1
- •2.5 Варіанти самостійного завдання №2
- •2.6 Приклади виконання завдання
- •2.6.1 Приклад завдання №1
- •2.6.2 Приклад завдання №2
- •3 Лабораторна робота № 3 марківські процеси з дискретними станами та неперервним часом
- •3.1 Потоки подій
- •3.2 Рівняння Колмогорова
- •3.3 Однорідні марківські процеси з дискретними станами та неперервним часом. Стаціонарний режим
- •3.4 Варіанти самостійного завдання №1
- •3.5 Варіанти самостійного завдання №2
- •3.6 Приклади виконання завдання
- •3.6.1 Приклад завдання №1
- •3.6.2 Приклад завдання №2
- •4 Рекомендована література
2.4 Варіанти самостійного завдання №1
Завдання:
дан
граф станів системи
.
В початковий момент часу
![]() система
знаходиться
у стані
.
Необхідно:
система
знаходиться
у стані
.
Необхідно:
а) визначити матрицю перехідних ймовірностей системи;
б) дати класифікацію станів системи;
в) знайти розподіл ймовірностей для перших чотирьох кроків.
2 |
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2.5 Варіанти самостійного завдання №2
Завдання:
дана
матриця перехідних ймовірностей
![]() системи
.
Необхідно:
системи
.
Необхідно:
а) побудувати граф станів системі ;
б) знайти граничні ймовірності станів.
2.5.1
|
2.5.2
|
2.5.3
|
2.5.4
|
2.5.5
|
2.5.6
|
2.5.7
|
2.5.8
|
2.5.9
|
2.5.10
|
2.5.11
|
2.5.12
|
2.5.13
|
2.5.14
|
2.5.15
|
2.5.16
|
2.5.17
|
2.5.18
|
2.5.19
|
2.5.20
|
2.6 Приклади виконання завдання
2.6.1 Приклад завдання №1
Дана система з дискретними станами та дискретним часом. Граф станів має вигляд:






В початковий момент
часу
система
знаходиться
у стані
![]() .
Необхідно:
.
Необхідно:
а) визначити матрицю перехідних ймовірностей системи;
б) дати класифікацію станів системи;
в) знайти розподіл ймовірностей для перших чотирьох кроків.
Розв’язання:
а) матриця перехідних ймовірностей:

б) стан
![]() є кінцевим, стан
є кінцевим, стан
![]() є джерелом, стани
і
є джерелом, стани
і
![]() −
транзитивні;
−
транзитивні;
в) так як при система знаходиться у стані , то
![]() ,
,
![]() ,
,
або
![]() .
.
За формулою
(2.12) при
![]() отримаємо розподіл ймовірностей станів
на першому кроці.
отримаємо розподіл ймовірностей станів
на першому кроці.

![]() ,
,
![]() ,
,
![]() .
.
Або, ![]() .
.
На другому кроці:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Або,
![]() .
.
Аналогічно знаходимо
![]() ,
,
![]() .
.

 .4.1
.4.1 .4.2
.4.2 .4.3
.4.3 .4.4
.4.4 .4.5
.4.5 .4.6
.4.6 .4.7
.4.7 .4.8
.4.8 .4.9
.4.9




 .4.10
.4.10
 .4.11
.4.11 .4.12
.4.12 .4.13
.4.13 .4.14
.4.14






 .4.15
.4.15 .4.16
.4.16 .4.17
.4.17 .4.18
.4.18 .4.1
.4.1 .4.20
.4.20