
- •8. Дифференциальные уравнения
- •8.1. Основные понятия и определения
- •8.2. Дифференциальные уравнения первого порядка.
- •Уравнения с разделяющимися переменными
- •Подставляем полученное соотношение в исходное уравнение
- •8.3. Дифференциальные уравнения второго порядка
- •8.4. Решение обыкновенных дифференциальных уравнений (оду)
- •8.4.1. Символьное (аналитическое) решение оду
- •8.4.2. Численные методы решения оду
Подставляем полученное соотношение в исходное уравнение
![]()
![]()
Из этого уравнения определим переменную функцию С1(х):
![]()
Интегрируя, получаем:
![]()
Подставляя это значение в исходное уравнение, получаем:
![]() .
.
Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.
При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.
Пример.
Решить уравнение
![]()
Сначала
приведем данное уравнение к стандартному
виду:
![]()
Применим
полученную выше формулу:
![]() . Тогда
. Тогда
![]() или
или
![]()
откуда
![]()
Уравнение Бернулли
Уравнением Бернулли называется уравнение вида
![]() (8.8)
(8.8)
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для
решения уравнения Бернулли применяют
подстановку
![]() ,
с помощью которой, уравнение Бернулли
приводится к линейному.
,
с помощью которой, уравнение Бернулли
приводится к линейному.
Для этого разделим исходное уравнение на yn.
![]()
Применим
подстановку, учтя, что
![]() .
.
![]() или
или
![]()
Т.е. получено линейное уравнение относительно неизвестной функции z.
Решение этого уравнения будем искать в виде:
![]()
![]()
Пример.
Решить уравнение
![]()
Разделим
уравнение на xy2:
![]()
Полагаем
![]()
![]() .
.
Полагая
![]() ,
найдём
,
найдём
![]()
![]()
![]() .
.
Произведя обратную подстановку, получаем:
![]()
Пример.
Решить уравнение
![]()
Разделим
обе части уравнения на
![]()
![]()
Полагаем
![]()
![]() .
.
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
![]()
![]()
Полагаем C = C(x) и подставляем полученный результат в линейное неодно-родное уравнение, с учетом того, что:
![]()
![]()
![]()
Получаем:
![]()
Применяя обратную подстановку, находим окончательный ответ:
![]() .
.
Задачи для самостоятельного решения
Решить задачу
Коши:
1)
![]() .
2)
.
2)
![]() .
.
3)
![]() .
4)
.
4)
![]() .
.
5)
![]() .
6)
.
6)
![]() .
.
7)
![]() . 8)
. 8)
![]() .
.
9)
![]() .
9)
.
9)
![]() .
.
10)
![]() ;
11)
;
11)
![]() .
.
8.3. Дифференциальные уравнения второго порядка
Дифференциальное уравнение второго порядка – это уравнение вида
![]() ,
(8.9)
,
(8.9)
где х
– независимая переменная, y
– искомая функция,
и
![]() -
соответ-ственно, её первая и вторая
производные.
-
соответ-ственно, её первая и вторая
производные.
Примеры дифференциальных уравнений второго порядка:
![]() - дифференциальное
уравнение движения материальной точки
массы m
под действием силы F
(x(t)
– закон движения).
- дифференциальное
уравнение движения материальной точки
массы m
под действием силы F
(x(t)
– закон движения).
![]() - уравнение
вынужденных колебаний динамических
систем.
- уравнение
вынужденных колебаний динамических
систем.
Следует также отметить, что большая часть дифференциальных уравнений, описывающих процессы для динамических систем, являются уравнениями второго порядка.
Далее мы будем рассматривать теорию дифференциальных уравнений второго порядка разрешенных относительно второй производной
![]() .
(8.10)
.
(8.10)
Как
и для уравнений первого порядка, не
существует общих методов решения
уравнения второго порядка. Для некоторых
важных классов функций
![]() такие методы известны.
такие методы известны.
Уравнения, допускающие понижение порядка
Для некоторых функций уравнение второго порядка (8.10) с помощью подходящей замены переменной может быть сведено к уравнению первого порядка.
1.0
Если правая часть уравнения содержит
только независимую пере-менную, то есть
уравнение имеет вид
![]() .
.
а)
Проще всего, решение такого уравнения
найти двукратным его интегрированием,
а именно, имеем
![]() ,
разделяя
переменные, получаем
,
разделяя
переменные, получаем
![]() , или
, или
![]() ,
откуда
,
откуда
![]() и последующее интегрирование даёт
и последующее интегрирование даёт
![]() .
.
В
результате искомое решение имеет вид
![]() .
.
Примеры.
1) Найти общее
решение уравнения
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
 ,
,
![]() ,
откуда
,
откуда
![]() .
.
2)
Найти общее решение уравнения
![]()
![]() ,
,
![]() ,
,
![]()
![]()
б). Иначе,
исходное дифференциальное уравнение
формально может быть сведено к уравнению
первого порядка с помощью замены
переменной
![]() .
.
2.0
Следующий случай, когда дифференциальное
уравнение второго порядка (8.10) сводится
к уравнению первого порядка, связан с
тем, что правая часть уравнения содержит
только независимую переменную x
и производную искомой функции
,
то есть уравнение (8.10.) имеет вид
![]() .
Сведение данного уравнения к уравнению
первого порядка достигается с помощью
замены переменной
.
А именно, имеем
.
Сведение данного уравнения к уравнению
первого порядка достигается с помощью
замены переменной
.
А именно, имеем
![]() или
или
![]() ,
пусть
,
пусть
![]() - общее решение предыдущего уравнения,
тогда искомое решение
исходного
уравнения
определяется
из решения уравнения первого порядка
- общее решение предыдущего уравнения,
тогда искомое решение
исходного
уравнения
определяется
из решения уравнения первого порядка
![]() .
.
Примеры.
1).
Найти общее решение уравнения
![]() .
.
Запишем
исходное уравнение в виде
![]() .
Обозначим
,
тогда
.
Обозначим
,
тогда
![]() или, разделяя переменные, находим
или, разделяя переменные, находим
![]() откуда
откуда
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
И, наконец, так как
.
И, наконец, так как
![]() ,
то
,
то
![]() и
и
![]() .
.
2).
Найти общее решение уравнения
![]() .
.
Обозначим
.
Тогда
![]() и для функции р(x)
получим уравнение первого порядка
и для функции р(x)
получим уравнение первого порядка
![]() .
Это уравнение с разделяющимися
переменными. Разделяя переменные и
интегрируя, получим
.
Это уравнение с разделяющимися
переменными. Разделяя переменные и
интегрируя, получим
![]() ,
,
![]() или
или
![]() .
.
Отсюда
![]() и
и
![]() .
Последний интеграл вычислим по частям,
полагая u =
lnx, dv
= dx. Тогда
du =1/x dx,
v = x
и
.
Последний интеграл вычислим по частям,
полагая u =
lnx, dv
= dx. Тогда
du =1/x dx,
v = x
и
![]()
3.0
Рассмотрим ещё один случай, когда
дифференциальное уравнение (8.10) допускает
снижение порядка. Пусть правая часть
уравнения (8.10) не содержит независимой
переменной х.
Т.е. имеет вид
![]() .
Вводится замена переменной
.
Вводится замена переменной
![]() ,
тогда по правилу дифференцирования
сложной функции
,
тогда по правилу дифференцирования
сложной функции
![]()
Пример.
Найти общее решение уравнения
![]()
Замена
переменной:
![]()
![]()
1)
![]()
Для
решения полученного дифференциального
уравнения произведем замену переменной:
![]() тогда
тогда
![]()
![]()
![]()
![]() .
.
С
учетом того, что
![]() ,
получаем:
,
получаем:
![]()
![]()
Общий
интеграл имеет вид:
![]()
2)
![]()
![]()
Таким образом, получили два общих решения.
Линейные дифференциальные уравнения второго порядка
Многие задачи в области механики, физики, электротехники, робото-техники, систем управления, химической технологии и других технических систем приводят к линейным дифференциальным уравнениям второго порядка.
Уравнения вида
![]() ,
(8.11)
,
(8.11)
где
![]() - заданные функции, называется линейным
ДУ второго порядка. Это
уравнение содержит неизвестную функцию
и её про-изводные
- заданные функции, называется линейным
ДУ второго порядка. Это
уравнение содержит неизвестную функцию
и её про-изводные
![]() в первой степени. Функции
в первой степени. Функции
![]() называются коэф-фициентами
уравнения (8.11), а
называются коэф-фициентами
уравнения (8.11), а
![]() - свободным
членом.
- свободным
членом.
Если
свободный член
![]() ,
то уравнение (8.11) называется линейным
однородным,
а если
,
то уравнение (8.11) называется линейным
однородным,
а если
![]() ,
то уравнение (8.11) неоднородно.
,
то уравнение (8.11) неоднородно.
Линейные однородные ДУ второго порядка
Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка:
![]() (8.12)
(8.12)
и установим некоторые свойства решений этого уравнения.
Теорема.
Если функции
![]() и
и
![]() являются решениями уравнения (8.12), то
решением этого уравнения является также
линейная комбинация этих функций
являются решениями уравнения (8.12), то
решением этого уравнения является также
линейная комбинация этих функций
![]() ,
(8.13)
,
(8.13)
где с1 и с2 - произвольнее постоянные.
Доказательство. Подставим функцию (8.13) и её производные в левую часть (8.12). Получим
![]() (
(![]() (
(![]()
![]()
![]() (
(![]()
![]()
![]() .
.
Таким образом,
функция
![]() является также является ре-шением
уравнения (8.12).
является также является ре-шением
уравнения (8.12).
Итак, функция вида у = с произвольными постоянными с1 и с2 является решением уравнения (8.12). Докажем в последствии, что (8.13) при некоторых условиях является общим решением (8.12). Для этого рассмотрим понятие линейной зависимости и линейной независимости функций.
Функции
![]() и
и
![]() называется линейно
зависимыми
на (a,b),
если существуют такие числа с1
и с2,
из которых хотя бы одно отлично от нуля,
что для любого
называется линейно
зависимыми
на (a,b),
если существуют такие числа с1
и с2,
из которых хотя бы одно отлично от нуля,
что для любого
![]() имеет место равенство
имеет место равенство
![]() .
(8.14)
.
(8.14)
Очевидно, что
если функции
и
линейно зависимы, то они пропорциональны.
Действительно, если
,
причём
![]()
и
![]() ,
то
,
то
![]() .
Верно и обратное.
.
Верно и обратное.
Функции и называется линейно независимыми на (a,b), если не существует таких чисел с1 и с2, из которых хотя бы одно отлично от нуля, что для любого имеет место равенство (8.14).
Другими словами, равенство (8.14) выполняется сразу для всех , если только с1 = с2 = 0.
Очевидно,
что если функции
и
линейно независимы, то их отношение
![]() ,
т.е. они не пропорциональны.
,
т.е. они не пропорциональны.
Так, например,
функции
![]() и
и
![]() линейно независимы на любом интервале
линейно независимы на любом интервале
![]() ,
поскольку
,
поскольку
![]() ,
а функции
,
а функции
![]() и
и
![]() линейно зависимы на любом интервале
,
так как
линейно зависимы на любом интервале
,
так как
![]() .
.
Признак линейной зависимости системы функций связан с так назы-ваемым определителем Вронского или вронскианом. Для двух дифферен-цируемых функций и вронскиан имеет следующий вид
W(x)
=
![]() .
.
Имеют место следующие теоремы.
Теорема 1. Если дифференцируемые функции и линейно зависимы на (a,b), то определитель Вронского на этом интервале равен нулю.
Доказательство.
Так как функций
и
линейно зависимы, то они пропорциональны
![]() = α
= α
![]() и
и
![]() = α
= α
![]() , тогда определитель Вронского
, тогда определитель Вронского
![]() =
=
![]() = 0.
= 0.
Теорема 2. Для того, чтобы две дифференцируемые функций и были бы линейно независимы на [a,b] необходимо и достаточно, чтобы определитель Вронского на этом сегменте был бы отличен от нуля.
![]() .
.
Теорема (о структуре общего решения ЛОДУ второго порядка) Если два решения и ЛОДУ линейно независимы, то их линейная комбинация
у =
является общим решением этого уравнения.
Доказательство. Так как и являются решениями уравнения (8.12), то их линейная комбинация у = также – решение этого уравнения. Остаётся доказать, что это решение общее, т.е., что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
![]() ,
(8.15)
,
(8.15)
Подставляем данные условия в решение , получим систему уравнений
![]() ,
(8.16)
,
(8.16)
относительно неизвестных с1 и с2.
Определитель этой системы
![]()
равен
значению вронскиана в точке х
= х0
. Но так
как
и
являются линейно независимыми на [a,b]
, то согласно теореме 2,
![]() .
А это означает, что система (8.16) имеет
единственное решение:
.
А это означает, что система (8.16) имеет
единственное решение:
![]() ,
,
![]() .
.
Решение
![]() является единственным частным решением
уравнения (8.12), удовлетворяющим начальным
условиям (8.15). Теорема доказана.
является единственным частным решением
уравнения (8.12), удовлетворяющим начальным
условиям (8.15). Теорема доказана.
Линейные однородные дифференциальные уравнения второго порядка
с постоянными коэффициентами
Рассмотрим частный случай ДУ (8.12), когда коэффициенты уравнения р и g являются постоянными величинами. Таким образом, дано линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка
![]() ,
(8.17)
,
(8.17)
где р и g постоянны.
Это равнение может иметь множество решений, однако среди них необходимо выделить два линейно независимых (базисных) решений.
Будем
искать решение уравнения (8.17) в виде
![]() ,
где k
- некоторое число. Подставляя эту функцию
в уравнение, получаем:
,
где k
- некоторое число. Подставляя эту функцию
в уравнение, получаем:
![]()
и после сокращения
этого равенства на
![]() ,
найдём, что число k
должно удовлетворять уравнению
,
найдём, что число k
должно удовлетворять уравнению
![]() .
(8.18)
.
(8.18)
Уравнение (8.18) называется характеристическим уравнением для дифференциального уравнения (8.17).
При решении характеристического уравнения может представиться три случая.
С
л у ч а й 1. Дискриминант характеристического
уравнения (8.18)
![]() ,
в этом случае уравнение (8.18) имеет два
неравных действительных корня k1
и k2
(
,
в этом случае уравнение (8.18) имеет два
неравных действительных корня k1
и k2
(![]() ). И частными решениями уравнения (8.17)
являются функции
). И частными решениями уравнения (8.17)
являются функции
![]() и
и
![]() .
Они образуют базисную систему решений
(линейно независимы), т.к. их вронскиан
.
Они образуют базисную систему решений
(линейно независимы), т.к. их вронскиан
W(x)
=
 .
.
Следовательно, общее решение уравнения (8.17) имеет вид
![]() .
(8.19)
.
(8.19)
С л у ч а й 2.
Дискриминант характеристического
уравнения (8.18)
![]() ,
в этом случае уравнение (8.18) имеет два
равных корня k1
= k2
=
,
в этом случае уравнение (8.18) имеет два
равных корня k1
= k2
=![]() .
И частным решением является лишь одно
решение
. Покажем, что наряду с
решением уравнения (8.17) будет также
функция
.
И частным решением является лишь одно
решение
. Покажем, что наряду с
решением уравнения (8.17) будет также
функция
![]() . Действительно, подставим функцию
в дифференциальное уравнение (8.17).
. Действительно, подставим функцию
в дифференциальное уравнение (8.17).
![]()
=![]() =
=
=
![]() .
.
Но
![]() ,
т.к. k1
есть корень уравнения (8.18);
,
т.к. k1
есть корень уравнения (8.18);
![]() ,
т.к. k1
=
.
Поэтому
,
т.к. k1
=
.
Поэтому
![]() , т.е функция
является ре-шением уравнения (8.17).
, т.е функция
является ре-шением уравнения (8.17).
Частные решения
и
образуют базисную систему решений:
определитель Вронского W(x)
=
![]() .
Следовательно, в этом случае общее
решение ЛОДУ является функция
.
Следовательно, в этом случае общее
решение ЛОДУ является функция
![]() .
(8.20)
.
(8.20)
С л у ч а й 3.
Дискриминант характеристического
уравнения (8.18)
![]() ,
в этом случае уравнение (8.18) имеет два
комплексных корня k1
=
,
в этом случае уравнение (8.18) имеет два
комплексных корня k1
=
![]() и k2
=
и k2
=
![]() (
(![]() ,
,
![]() ). И частными решениями уравнения (8.17)
являются функции
). И частными решениями уравнения (8.17)
являются функции
![]() и
и
![]() .
В этом случае легко убедиться, что
функции
.
В этом случае легко убедиться, что
функции
![]() и
и
![]() являются решениями уравнения (8.17) и
образуют базисную систему решений.
Прежде всего, убедимся, что эти функции
и
являются решениями дифференциального
уравнения (8.17). Подставим значение
в уравнение:
являются решениями уравнения (8.17) и
образуют базисную систему решений.
Прежде всего, убедимся, что эти функции
и
являются решениями дифференциального
уравнения (8.17). Подставим значение
в уравнение:
![]()
=
![]() +
+
+
![]() =
=
![]() .
.
Но
и
![]() ,
тогда
,
тогда
![]() = 0 и
= 0 и
![]() = 0. Поэтому
= 0. Поэтому
![]() , т.е функция
является решением уравнения (8.17).
Аналогичным образом доказывается, что
функция
также есть решение уравнения (8.17). Кроме
того, эти функции
и
являются линейно независимыми: их
вронскиан W(x)
=
, т.е функция
является решением уравнения (8.17).
Аналогичным образом доказывается, что
функция
также есть решение уравнения (8.17). Кроме
того, эти функции
и
являются линейно независимыми: их
вронскиан W(x)
=
![]() .
Таким образом, общее решение уравнения
(8.17) в данном случае запишется в виде
.
Таким образом, общее решение уравнения
(8.17) в данном случае запишется в виде
![]() =
=
![]() (8.21)
(8.21)
Примеры.
1.
Решить уравнение
![]()
Характеристическое
уравнение:
![]()
Общее
решение:
![]()
2. Решить уравнение
![]()
Характеристическое уравнение:
![]()
![]()
Общее
решение:
![]()
2.
Решить уравнение
![]()
Характеристическое
уравнение:
![]()
Общее
решение:
![]()
Линейные неоднородные дифференциальные уравнения второго
порядка (ЛНДУ)
Так называются уравнения вида
![]() ,
(8.22)
,
(8.22)
где p(x), g(x), f(x) – заданные, непрерывные на (a,b) функции.
Соответствующее ему уравнение (с нулевой правой частью)
![]() (8.23)
(8.23)
называется однородным уравнением.
Теорема
(о структуре общего решения ЛНДУ). Общее
решение уравнения
![]() (8.22) представляется суммой общего решения
(8.22) представляется суммой общего решения
![]() соответствующего
ему однородного уравнения (8.23) и частного
решения
соответствующего
ему однородного уравнения (8.23) и частного
решения
![]() неоднородного уравнения (8.22)
неоднородного уравнения (8.22)
![]() .
(8.24)
.
(8.24)
Доказательство.
Так как
- общее решение однородного уравнения
(8.23), а
- частное решение неоднородного уравнения
(8.22), то
![]() и
и
![]() .
.
В таком случае
![]()
![]()
+ (![]() .
.
А это означает,
что функция
![]() является решением уравнения (8.22). Теперь
необходимо показать, что функция
является решением уравнения (8.22). Теперь
необходимо показать, что функция
![]() (8.25)
(8.25)
является общим решением уравнения (8.22). Убедимся, что из решения (8.25)
можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
, (8.26)
Подставляем данные условия в решение (8.25), получим систему уравнений
![]() ,
,
относительно неизвестных с1 и с2.
Определителем этой системы
равен
значению вронскиана в точке х
= х0
. Но так как
и
являются линейно независимыми на (a,b)
, то
.
А это означает, что система (8.16) имеет
единственное решение:
![]() ,
,
![]() .
.
Решение
![]() является единственным частным решением
уравнения (8.22), удовлетворяющим начальным
условиям (8.26). Теорема доказана.
является единственным частным решением
уравнения (8.22), удовлетворяющим начальным
условиям (8.26). Теорема доказана.
Метод вариации произвольных постоянных
Рассмотрим
ЛНДУ (8.22). Его общее решение представляется
суммой общего решения у0
однородного уравнения (8.23) и частного
решения
![]() неоднородного уравнения (8.22). Если
известно общее решение у0
однородного уравнения, то частное
решение
можно найти методом
вариации произвольных постоянных,
сущность которого заключается в
следующем. Пусть
неоднородного уравнения (8.22). Если
известно общее решение у0
однородного уравнения, то частное
решение
можно найти методом
вариации произвольных постоянных,
сущность которого заключается в
следующем. Пусть
![]() - общее решение однородного уравнения.
Заменим в этом выражении постоянные
с1
и с2
неизвестными функциями с1(х)
и с2(х)
так, чтобы
- общее решение однородного уравнения.
Заменим в этом выражении постоянные
с1
и с2
неизвестными функциями с1(х)
и с2(х)
так, чтобы
![]() было бы решением уравнения (8.22). Найдём
производную
было бы решением уравнения (8.22). Найдём
производную
![]() .
.
Подберём функции с1(х) и с2(х) так, чтобы
![]() .
.
Тогда
![]() ,
,
![]() .
.
Подставляя выражения
,
![]() и
и
![]() в уравнение (8.22), получим
в уравнение (8.22), получим
![]() +
+
+ р(х)[![]() ]
+ q(x)
[
]
+ q(x)
[![]() ]
= f(x),
]
= f(x),
bли
с1(х)∙[![]() ]
+
]
+
+ с2(х)∙[![]() ]
+
]
+
![]() /
/
Так как и - решения уравнения (8.23), то выражения в квадратных скобках равны нулю, то
. (8.27)
Таким образом, функция будет частным решением уравнения (8.22), если функции с1(х) и с2(х) удовлетворяют системе
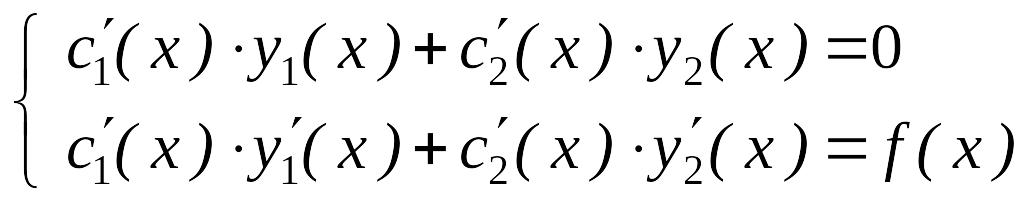 ,
(8.28)
,
(8.28)
Определитель этой
системы – вронскиан
,
так как функции
и
линейно независимы. Поэтому система
(8.28) имеет единственное решение:
![]() и
и
![]() .
Интегрируя эти функции, находим с1(х)
и с2(х),
в результате выражение
является частным решением неоднородного
уравнения (8.22).
.
Интегрируя эти функции, находим с1(х)
и с2(х),
в результате выражение
является частным решением неоднородного
уравнения (8.22).
ЛНДУ второго порядка с постоянными коэффициентами
Рассмотрим дифференциальное уравнение
![]() ,
(8.29)
,
(8.29)
где p и g постоянные величины, а f(x) – заданная функция.
Согласно теореме о структуре общего решения ЛНДУ оно представляется суммой общего решения у0 соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения с постоянными коэффициентами рассмотрено раннее в соответствующем разделе.
Что касается определения частного решения неоднородного уравнения с постоянными коэффициентами, то оно может быть определено с помощью метода вариации произвольных постоянных, описанного в предыдущем разделе. Однако если в правой части уравнения (8.29) - многочлен, либо показательная функция, либо тригонометрическая функция sinβx или cos βx, либо линейная комбинация перечисленных функций, то частное решение может быть найдено методом неопределённых коэффициентов, не содержащим процедуру интегрирования. Общий подход здесь таков: частное решение неоднородного уравнения, как правило, ищется в том же виде, какова его правая часть (то есть, функция f(x)). Однако, за этим “как правило” кроются многочисленные исключения.
Рассмотрим различные виды правых частей уравнения (8.29)
1. Если правая часть уравнения есть многочлен степени n f(x)=Pn(x) ) и x = 0 не является корнем характеристического уравнения, то частное решение так же следует искать в виде многочлена степени n (x)=Qn(x). Если же число x = 0 является корнем характеристического уравнения кратности r, то частное решение следует искать в виде (x)=xr Qn(x).
2. Если правая часть
уравнения имеет вид
![]() и число m
не является корнем характеристического
уравнения, то частное решение следует
искать в виде
(x)=Аеmx.
Если же m
является корнем характеристического
уравнения кратности r
, то
(x)=А
xrеmx.
и число m
не является корнем характеристического
уравнения, то частное решение следует
искать в виде
(x)=Аеmx.
Если же m
является корнем характеристического
уравнения кратности r
, то
(x)=А
xrеmx.
3. Если правая часть
уравнения имеет вид
![]() и число m
не является корнем характеристического
уравнения, то частное решение следует
искать в виде
и число m
не является корнем характеристического
уравнения, то частное решение следует
искать в виде
![]() .
Если же m
является корнем характеристического
уравнения кратности r
, то частное решение следует искать в
виде
.
Если же m
является корнем характеристического
уравнения кратности r
, то частное решение следует искать в
виде
![]() .
Даже в случае, когда правая часть
уравнения содержит только синус, либо
только косинус, частное решение все
равно следует искать в виде комбинации
и синуса и косинуса.
.
Даже в случае, когда правая часть
уравнения содержит только синус, либо
только косинус, частное решение все
равно следует искать в виде комбинации
и синуса и косинуса.
4. Если правая часть уравнения есть сумма, или произведение функций, рассмотренных выше, то частное решение следует искать в виде суммы, или произведения, соответствующих частных решений.
Пример 1.
Решить задачу Коши
![]() ,
y(0)
= 2,
,
y(0)
= 2,
![]() .
.
Решение. Сначала найдем общее решение однородного уравнения
![]() .
Его характеристическое уравнение
.
Его характеристическое уравнение
![]() имеет корни k1
= k2
= 1, поэтому общее решение однородного
уравнения имеет вид
имеет корни k1
= k2
= 1, поэтому общее решение однородного
уравнения имеет вид
![]() .
Правая часть неоднородного уравнения
есть многочлен первой степени f(x)=P1(x)
= x
+ 1. Поскольку ноль не является корнем
характеристического уравнения, то
частное решение неоднородного уравнения
так же будем искать в виде многочлена
первой степени
(x)=
Q1(x)
= Ax
+ B.
Подберем константы А
и В
так, чтобы функция
удовлетворяла неоднородному уравнению.
Для этого подставим функцию
(x)=Q1(x)
= Ax
+ B
и ее производные
.
Правая часть неоднородного уравнения
есть многочлен первой степени f(x)=P1(x)
= x
+ 1. Поскольку ноль не является корнем
характеристического уравнения, то
частное решение неоднородного уравнения
так же будем искать в виде многочлена
первой степени
(x)=
Q1(x)
= Ax
+ B.
Подберем константы А
и В
так, чтобы функция
удовлетворяла неоднородному уравнению.
Для этого подставим функцию
(x)=Q1(x)
= Ax
+ B
и ее производные
![]() в уравнение
,
получим
в уравнение
,
получим
-2 А + А x + B = х + 1 или Ax + (-2 A + B) = x + 1.
Последнее равенство должно выполняться при всех значениях х, что возможно лишь в том случае, когда равны коэффициенты при одинаковых степенях х в его левой и правой частях. Приравнивая соответствующие коэффициенты, получим систему линейных уравнений для определения величин А и В
![]()
Отсюда А = 1, В = 3 и, значит, частным решением неоднородного уравнения является функция (x)= x + 3. Общее решение уравнения имеет вид
y(x)
= y0(x)
+
![]()
Теперь
подберем константы c1
и c2
так, чтобы эта функция удовлетворяла
заданным начальным условиям. Поскольку
y(0)
= 2,
то, подставив в функцию
и
в ее производную
![]() заданные
начальные условия, получим систему
уравнений для определения постоянных
c1
и c2
заданные
начальные условия, получим систему
уравнений для определения постоянных
c1
и c2
![]()
Отсюда c1 = -1 и c2 = -3. Значит, решением задачи является функция
![]() .
.
Пример
2. Найти общее
решение уравнения
![]() .
.
Решение.
Корни характеристического уравнения
![]() k1
= k2
= -1 равны между собой, поэтому общее
решение однородного уравнения имеет
вид
k1
= k2
= -1 равны между собой, поэтому общее
решение однородного уравнения имеет
вид
![]() .
Правая часть уравнения есть функция
типа aemx
со значением m
= -1, которое является корнем
характеристического уравнения кратности
два m = k1
= k2
= -1 . Поэтому, частное решение уравнения
будем искать в виде
.
Правая часть уравнения есть функция
типа aemx
со значением m
= -1, которое является корнем
характеристического уравнения кратности
два m = k1
= k2
= -1 . Поэтому, частное решение уравнения
будем искать в виде
![]() .
Найдем производные этой функции
.
Найдем производные этой функции
![]() ,
,
![]()
и подставим эти производные и саму функцию в исходное уравнение
![]() +2(
+2(![]()
![]() ,
,
![]()
Последнее
равенство возможно лишь в том случае,
когда A
= 5/2. Таким образом, частным решением
уравнения является функция
![]() , а его общее решение имеет вид y(x)
= y0(x)
+
, а его общее решение имеет вид y(x)
= y0(x)
+
![]()
Пример 3.
Найти общее решение уравнения
![]() .
.
Решение.
Корни характеристического уравнения
![]() равны
равны
![]() ( α = 0, β = 3), поэтому общее решение
однородного уравнения имеет вид
( α = 0, β = 3), поэтому общее решение
однородного уравнения имеет вид
![]() .
Правая часть нашего уравнения есть
комбинация синуса и косинуса
при a
= 5, b
= 0 и m
= 2.
.
Правая часть нашего уравнения есть
комбинация синуса и косинуса
при a
= 5, b
= 0 и m
= 2.
Так
как число 2i не является корнем
характеристического уравнения, то
частное решение уравнения будем искать
в виде
![]() .
Найдем производные этой функции
.
Найдем производные этой функции
![]() ,
,
![]()
и подставим их вместе с функцией в исходное уравнение
![]() +
9 ∙
+
9 ∙![]() =
=
![]() ,
,
![]() =
=
![]() .
.
Последнее
равенство возможно лишь в том случае,
когда A
= 1 и B
= 0. Значит, частным решением уравнения
является функция
![]() ,
а его общее решение имеет вид
,
а его общее решение имеет вид
y(x)
= y0(x)
+
![]()
Пример 4.
Найти общее решение уравнения
![]() .
.
Решение.
Здесь характеристическое уравнение
![]() имеет корни
имеет корни
![]() ,
,
![]() .
Общее решение однородного уравнения
таково:
.
Общее решение однородного уравнения
таково:
![]() .
В правой части исходного уравнения –
произведение показательной и
тригонометрической функций. Число
.
В правой части исходного уравнения –
произведение показательной и
тригонометрической функций. Число
![]() не является корнем характеристического
уравнения, поэтому частное решение ищем
в виде
не является корнем характеристического
уравнения, поэтому частное решение ищем
в виде
![]() .
Дифференцируя и подставляя в уравнение,
получим
.
Дифференцируя и подставляя в уравнение,
получим
![]() .
.
Приравнивая коэффициенты при cosx и sinx, находим
![]() ,
,
![]() ,
,
откуда A=3/10,
B
= 3/5. Таким образом, частное и общее
решения соответственно:
![]()
и y(x)
=
![]() =
=
![]()
Задачи для самостоятельного решения
Решить задачу Коши:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() .
.
