
- •Постоянный ток
- •§ 1.1. Законы Кирхгофа.
- •§ 1.2. Примеры использования законов Кирхгофа
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12. Метод наложения (метод суперпозиции).
- •§2 Переменный ток
- •§2.1. Синусоидальные ток и напряжение. Символический метод
- •Немного о комплексных числах
- •Показания приборов
- •Векторные диаграммы – фазовые соотношения между величинами
- •Мощность в цепи переменного тока
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •Метод симметричных составляющих
- •Переходные процессы Переходные процессы в простейших цепях
- •Кассический метод расчета переходного процесса Первый и второй законы коммутации, Понятия о зависимых и независимых начальные условиях
- •Метод расчета переходных процессов в цепи переменный тока
- •Переходные процессы в цепи второго порядка
- •Операторный метод расчёта переходных процессов
- •Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Формулы для определения напряжения и тока в любой точке линии через комплексы тока и напряжения в начале линии
- •Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •Линии без потерь
- •Коэффициент отражения
- •Действующие значения напряжения и тока вдоль линии без потерь
- •Стоячие волны
- •Входное сопротивление линии без потерь при холостом ходе
- •Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
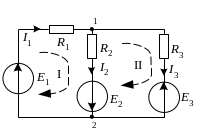
§ 1.2. Примеры использования законов Кирхгофа
Рис. 6 |
 Для
определения токов в электрической схеме
использовать правило преобразования
параллельно и последовательно соединённых
сопротивлений можно не всегда. Например,
для цепи представленной на рис. 6, это
мешают сделать ЭДС
Для
определения токов в электрической схеме
использовать правило преобразования
параллельно и последовательно соединённых
сопротивлений можно не всегда. Например,
для цепи представленной на рис. 6, это
мешают сделать ЭДС
Схема имеет три ветви, следовательно, необходимо записать три уравнения. Записываем одно уравнение по первому закону Кирхгофа. Например, для второго узла:
![]() . (13)
. (13)
Два недостающих уравнения записываем по второму закону Кирхгофа для первого и второго контуров соответственно:
 . (14)
. (14)
Запишем уравнения (13) и (14) в виде системы уравнений, предварительно правильно сгруппировав коэффициенты при неизвестных, в результате получаем формальное решение:
 . (15)
. (15)
Рассмотрим пример с числовыми данными.
Р |
![]() Схема
имеет шесть ветвей, следовательно,
необходимо составить шесть уравнений.
Три уравнения (Y-1=3) по
первому закону Кирхгофа (1-ЗК) и три
уравнения по второму закону Кирхгофа
(2-ЗК). Для узлов 1,2 и 3 соответственно
записываем по 1-ЗК:
Схема
имеет шесть ветвей, следовательно,
необходимо составить шесть уравнений.
Три уравнения (Y-1=3) по
первому закону Кирхгофа (1-ЗК) и три
уравнения по второму закону Кирхгофа
(2-ЗК). Для узлов 1,2 и 3 соответственно
записываем по 1-ЗК:
 . (16)
. (16)
До контуров I , II и III используем 2-ЗК:
 (17)
(17)
Перепишем в матричном виде и подставим числовые значения. В результате получаем:
 (18)
(18)
§ 1.3. Матрично-топологический метод
Рис 8 |
 Когда
ветвей и узлов в схеме много, решение
методом Кирхгофа становится утомительным,
потому что приходится составлять
алгебраические уравнения высокого
порядка. Поэтому в электротехнике
существуют методы, позволяющие понизить
порядок системы линейных алгебраических
уравнений. Такие методы называются
матрично–топологическими. Такие методы
особенно удобны для использования
компьютерных вычислений.
Когда
ветвей и узлов в схеме много, решение
методом Кирхгофа становится утомительным,
потому что приходится составлять
алгебраические уравнения высокого
порядка. Поэтому в электротехнике
существуют методы, позволяющие понизить
порядок системы линейных алгебраических
уравнений. Такие методы называются
матрично–топологическими. Такие методы
особенно удобны для использования
компьютерных вычислений.
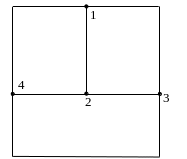
Рассмотрим использование матрично–топологического метода для схемы, приведённой на рисунке 7.
Прежде всего, рисуют ненаправленный (неориентированный) топологический граф схемы (рис. 7), на котором видно восемь ветвей и четыре узла. Затем задают направления токов, и граф становится направленным (ориентированным). Теперь, можно составить узловую матрицу, задавшись базовым узлом. Базовый узел – это узел, потенциал которого, равен некой постоянной величине, в частности нулю. Пусть, например, четвертый узел будет базовым узлом. Тогда сформируем узловую матрицу A по следующему правилу: если ток ветви подтекает к узлу, то ставим -1, если ток ветви оттекает от узла, то ставим 1, если ветвь не имеет связи с узлом, то ставим 0.
Рис 9. |
1 2 3 Узлы |
Ветви 1 2 3 4 5 6
|
Составим теперь матрицу контуров B по следующему правилу: если ветвь не входит в контур то ставим 0, если ветвь входит в контур, то ставим 1 в случае совпадения направления обхода контура с направлением тока, и ставим -1 в противном случае.
I II III Контуры |
Ветви 1 2 3 4 5 6
|
Если узловая и контурная матрицы составлены правильно, то их произведения должны равняться нулевой матрице:

Важными являются также диагональная матрица сопротивлений и проводимостей, а также и матрица ЭДС

Матрица ЭДС формируется по следующему правилу: если ЭДС в ветви отсутствует, то ставим 0, если направление ЭДС совпадает с направлением тока в ветви, то ставим ЭДС с положительным знаком, в противном случае ставим ЭДС с отрицательным знаком.
Лекция № 2

 ис.
7
ис.
7

