2.4.5. Математические ожидания и дисперсии.
В случае, когда задано совместное распределение вероятностей системы двух ДСВ, математические ожидания и дисперсии определяются по формулам:
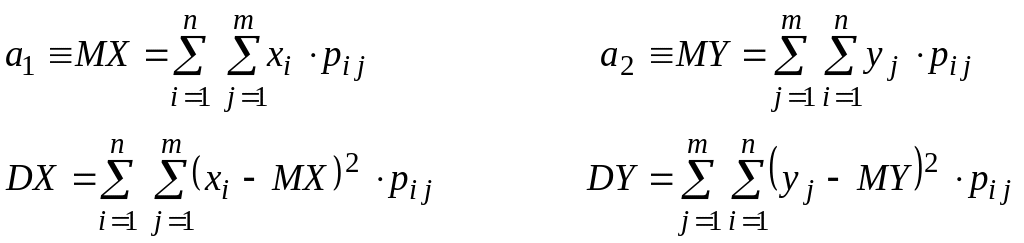
В случае двух НСВ
знаки
заменяются на
, а рij
– на
.
Условное математическое ожидание для НСВ:
Оно
называется уравнением (функцией)
регрессии Y
на X.
Аналогично
определяется уравнение регрессии X
на Y,
т. е.
Условная дисперсия для НСВ:
Аналогично
определяется
.
Для ДСВ знак ∫
заменяется на Σ, а
– на
.
Условные математическое ожидание и дисперсия характеризуют случайную величину Y при фиксированном значении параметра x или наоборот.
2.4.6. Показатели статистической зависимости двух св
1. Ковариация (корреляционный момент):
В частности, для системы из двух непрерывных случайных величин:
Свойства:
1)
2) КХХ≡
3)
4)
5)
Если X
и Y
– независимы, то они некоррелированы,
т. е.
(обратное бывает не справедливо).
Эти свойства легко
доказываются, если воспользоваться
общей формулой для ковариации и свойствами
математического ожидания, в частности,
если вспомнить, что для независимых СВ
.
Пример.
Пусть Y
и X
связаны зависимостью
,
где
независимые
СВ,
.
Тогда
.
Вывод: зависимые X и Y оказались некоррелированными.
2. Коэффициент корреляции:
Свойства: 1)
,
2)
3)
тогда и только тогда,
когда
где
причем
,
если
и
,
если
4) Для независимых
X
и Y
(так как
)
Докажем второе и
третье свойство. Пусть
,
где
независимые
СВ. Тогда, используя свойства дисперсии,
получим: DY=a2DX+D
,
так как Db=0;
D(XY)=D(X
)=
+D
.
Применим формулы:
cov(X,Y)=
;
D(XY)=DX+DY2cov(X,Y).
Подставляя в последнюю предыдущие выражения, получим:
+D
=DX+a2DX+D
2
;
=
.
Отсюда
.
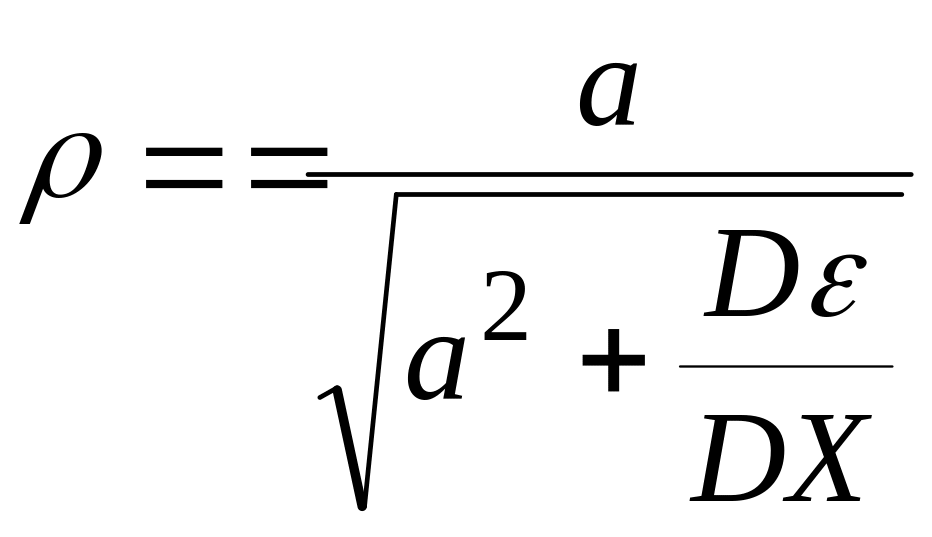Так как знаменатель
не меньше, чем
,
то получаем неравенство:
.
Если
т.е.
D
=0,
то имеем:
.
Коэффициент корреляции характеризует степень тесноты линейной связи между двумя случайными величинами.
3. Коэффициенты детерминации и корреляционные отношения
Коэффициенты детерминации определяются по формулам:
;
,
где
– одномерные плотности вероятности;
;
;
,
– условные математические ожидания;
,
– условные дисперсии.
Часто
=σ2=
const,
тогда
=1–
.
Можно показать,
что 0
ρ2
η2
1,
где ρ
– коэффициент корреляции. Равенство
η2=ρ2
имеет место
лишь при линейных функциях
,
.
Корреляционным
отношением называют корень квадратный
из коэффициента детерминации, взятый
со знаком плюс, т.е. – величину η=
.
2.4.7. Двумерное нормальное распределение.
Плотность вероятности:
,
где
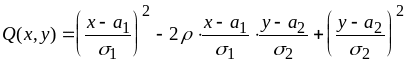
В общем случае
график f(x,y)
имеет вид сплюснутого с боков колокола,
в сечениях которого – эллипсы:
.
При
главные оси эллипсов параллельны осям
координат. Если
и
,
то сечениями являются окружности.
Пользуясь формулами
в п.2.4.5 и п.2.4.6, можно определить, что
коэффициент
корреляции.
Если , то, подставляя этот ноль в формулу для двумерной плотности распределения, получим: , т. е. для нормального распределения из некоррелированности случайных величин следует их независимость.
Условную плотность
распределения
нетрудно получить, используя формулы
для одномерного и двумерного нормального
распределений:
,
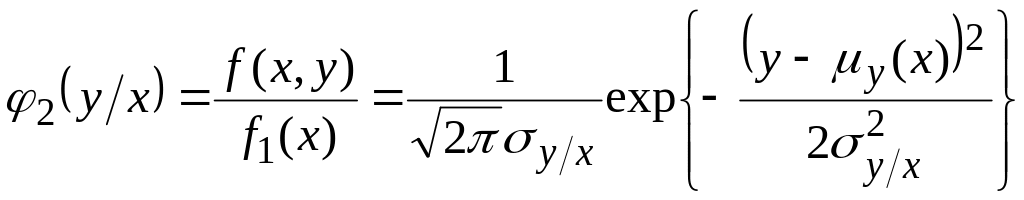где условное математическое ожидание и условная дисперсия:
т. е. уравнение
регрессии
является линейной функцией, а
Аналогично можно
определить условную плотность
распределения
.
Второе уравнение
регрессии:
Оба уравнения регрессии можно записать иначе:
Уравнения этих
прямых проходят через точку
и совпадают только при детерминированной
зависимости между X
и Y
, т.е. при
.