
- •§ 1 Топология п.1 Пространство
- •П.2 Открытые и замкнутые множества в метрическом пространстве
- •§ 2 Функции многих переменных п.1 Предел функции многих переменных
- •П.2 Непрерывность функции многих переменных
- •П.3 Свойства непрерывных функций
- •§ 3 Дифференцируемость функций многих переменных п.1 Частные производные
- •П.2 Дифференцируемость функций многих переменных
- •П.7 Касательная плоскость к графику функции двух переменных. Геометрический смысл дифференциала
- •П.8 Производная по направлению. Градиент
- •П.9 Частные производные и дифференциалы высших порядков
- •П.10 Формула Тейлора для функций нескольких переменных
- •§ 4 Неявные функции п.1 Определения
- •П.2 Существование, непрерывность и дифференцируемость неявной функции
- •П.3 Неявная функция нескольких переменных
- •§ 5 Локальный экстремум функции нескольких переменных п.1 Определения
- •П.2 Некоторые сведения о квадратичных формах
- •П.3 Достаточные условия локального экстремума
- •§ 6 Условный экстремум п.1 Определения
- •П.2 Прямой метод отыскания точек условного экстремума
- •П.3 Метод множителей Лагранжа
- •Алгоритм нахождения точек условного экстремума методом Лагранжа
П.3 Достаточные условия локального экстремума
Второй дифференциал
функции
![]() в точке
записывается в виде:
в точке
записывается в виде:
![]() .
.
Отсюда видно, что
![]() является квадратичной формой от
перемен-ных
является квадратичной формой от
перемен-ных
![]() ,
а частные производные
,
а частные производные
![]() – коэффициентами этой квадратичной
формы.
– коэффициентами этой квадратичной
формы.
Теорема (достаточные условия экстремума) Пусть функция имеет в окрестности точки непрерывные частные производные второго порядка и пусть . Тогда:
1) если второй дифференциал есть положительно определенная квадратичная форма, то – точка строгого минимума функции ;
2) если
![]() –
отрицательно определенная квадратичная
форма, то
–
точка строгого максимума функции
;
–
отрицательно определенная квадратичная
форма, то
–
точка строгого максимума функции
;
3) если – знакопеременная квадратичная форма, то функция не имеет экстремума в точке .
Замечание. Если для функции двух переменных обозначить
![]() ,
то:
,
то:
если
 ,
то функция
в точке
имеет экстремум (максимум при
,
то функция
в точке
имеет экстремум (максимум при
 и минимум при
и минимум при
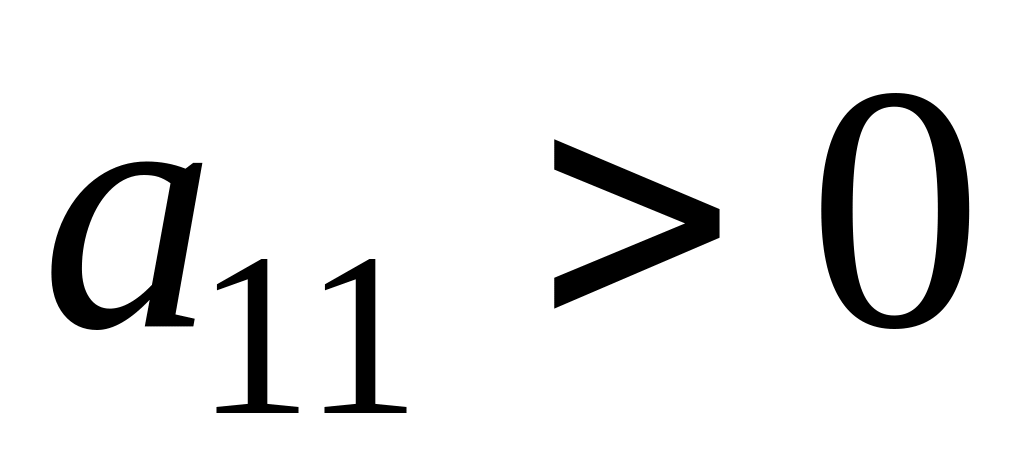 );
);если
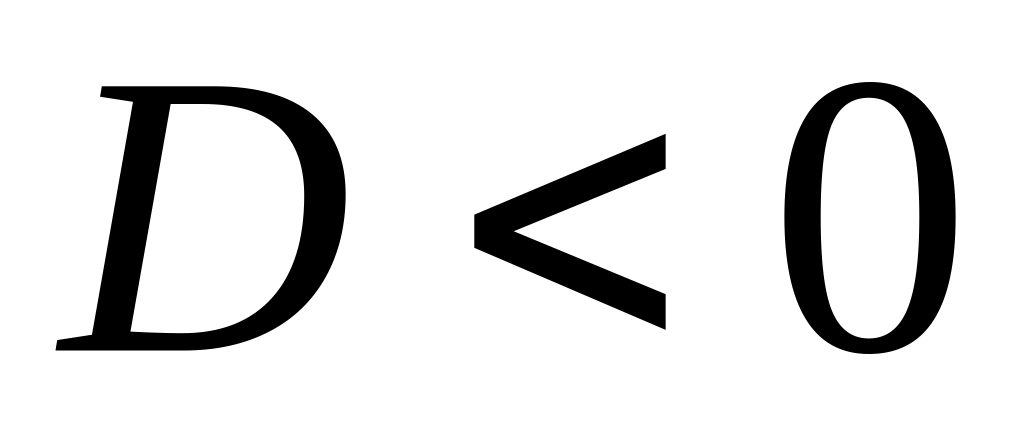 ,
то функция
не имеет экстремума;
,
то функция
не имеет экстремума;если
 ,
то функция
в точке
может иметь экстремум, а может и не
иметь. В этом случае нужны дополнительные
исследования.
,
то функция
в точке
может иметь экстремум, а может и не
иметь. В этом случае нужны дополнительные
исследования.
§ 6 Условный экстремум п.1 Определения
Пусть на открытом
множестве
![]() заданы функции
заданы функции
![]() ,
причем
,
причем
![]() .
Пусть Е –
множество точек множества G,
удовлетворяющих системе уравнений:
.
Пусть Е –
множество точек множества G,
удовлетворяющих системе уравнений:
![]() .
(1)
.
(1)
Уравнения (1) будем называть уравнениями связей.
О. Точка
![]() называется точкой
условного минимума функции
называется точкой
условного минимума функции
![]() при наличии связей (1), если найдется
такая окрестность
при наличии связей (1), если найдется
такая окрестность
![]() ,
что для
,
что для
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Аналогично определяются точки строгого условного минимума, условного максимума, строгого условного максимума.
Точки условного максимума и условного минимума называются точками условного экстремума.
П.2 Прямой метод отыскания точек условного экстремума
Допустим, что из
системы уравнений (1) можно выразить
какие-либо m
переменных
![]() через остальные переменные. Тогда,
подставив вместо соответствующих
переменных
их выражения через остальные n-m
переменных
в функцию
,
получим функцию F
от n-m
переменных.
через остальные переменные. Тогда,
подставив вместо соответствующих
переменных
их выражения через остальные n-m
переменных
в функцию
,
получим функцию F
от n-m
переменных.
Задача на нахождение условного экстремума сведена к задаче нахождения обычного (локального) экстремума функции F, зависящей от n-m переменных.
Пример
Найти точки
условного экстремума функции
![]() ,
если
,
если
![]() .
.
Решение. Выразим
из уравнения связи
![]() .
Тогда
.
Тогда
![]() .
Отсюда
.
Отсюда
![]() ,
,
![]() при
при
![]() .
Так как
.
Так как
![]() ,
то
– точка условного максимума.
,
то
– точка условного максимума.
Этот метод нахождения условного экстремума не всегда эффективен ввиду трудности разрешения уравнений связей относительно m переменных.
Геометрический смысл задачи на условный экстремум.
Соотношения (1)
задают в пространстве
некоторую поверхность. Если равенства
(1) заданы с помощью независимых переменных
![]() и
и
![]() ,
то данная поверхность имеет размерность
n-m.
Задача состоит в том, чтобы среди точек,
лежащих на данной поверхности, найти
те, в которых функция принимает наибольшее
или наименьшее значения.
,
то данная поверхность имеет размерность
n-m.
Задача состоит в том, чтобы среди точек,
лежащих на данной поверхности, найти
те, в которых функция принимает наибольшее
или наименьшее значения.
П.3 Метод множителей Лагранжа
Рассмотрим функцию n+m переменных:
![]() ,
где
,
где
![]() ,
,
![]() .
.
Числа
![]() называются множителями
Лагранжа, а
функция
называются множителями
Лагранжа, а
функция
![]() называется функцией
Лагранжа.
называется функцией
Лагранжа.
О. Точка
![]() называется стационарной
точкой функции Лагранжа,
если
называется стационарной
точкой функции Лагранжа,
если
![]() ,
… ,
,
… ,
![]() ,
,
![]() ,
… ,
,
… ,
![]() .
.
Теорема 1
(Лагранжа. Необходимое условие условного
экстремума) Пусть
– точка условного экстремума функции
при наличии связей (1) и пусть функции
![]() ,
,
![]() непрерывно-дифференцируемы в окрестности
точки
,
причем в точке
ранг матрицы Якоби
непрерывно-дифференцируемы в окрестности
точки
,
причем в точке
ранг матрицы Якоби
 равен m.
(*)
равен m.
(*)
Тогда найдутся
такие множители Лагранжа
![]() ,
что
будет стационарной точкой функции
Лагранжа.
,
что
будет стационарной точкой функции
Лагранжа.
Обозначим
![]() – второй дифференциал функции Лагранжа,
вычисленный по переменным
в точке
– второй дифференциал функции Лагранжа,
вычисленный по переменным
в точке
![]() ,
т.е.
,
т.е.
![]() .
.
Обозначим через
![]() следующее множество в
:
следующее множество в
:
 .
.
Теорема 2
(Необходимое условие точки условного
минимума) Пусть
–
точка условного экстремума функции
при наличии связей (1) и пусть функции
,
имеют непрерывные частные производные
II
порядка в окрестности точки
,
причем в точке
ранг матрицы Якоби (*) равен m.
Тогда найдутся такие множители Лагранжа
такие, что
является стационарной точкой функции
Лагранжа, а
![]() при
при
![]() .
.
Теорема 3
(достаточные условия условного
экстремума) Пусть функции
,
имеют непрерывные частные производные
II
порядка в окрестности точки
![]() ,
причем в точке
ранг матрицы Якоби (*) равен m,
и пусть
является стационарной точкой функции
Лагранжа
,
причем в точке
ранг матрицы Якоби (*) равен m,
и пусть
является стационарной точкой функции
Лагранжа
![]() .
.
Тогда если
![]() есть положительно определенная
квадратичная форма при
,
то
является точкой условного строгого
минимума функции
при наличии связей (1).
есть положительно определенная
квадратичная форма при
,
то
является точкой условного строгого
минимума функции
при наличии связей (1).
Если есть отрицательно определенная квадратичная форма при , то является точкой условного строгого максимума функции при наличии связей (1).
Если есть неопределенная квадратичная форма при , то не является точкой условного экстремума функции при наличии связей (1).
