Математический анализ

Множества.

Множество – это совокупность однородных объектов, называемых элементами.

Множества могут состоять из чисел, векторов, функций и других объектов.

Множества обозначаются прописными буквами – А, В, С,, а их элементы строчными - буквами a, b, c.

Если элемент a принадлежит множеству А, то это обозначается как , если элемент a не принадлежит множеству А, то это обозначается .

Множество, не содержащее ни одного элемента, называется пустым и обозначается .

Множество В называется подмножеством множества А, если все элементы множества В принадлежат множеству А. Это обозначается как операция включения: .

Множества называются равными, если их элементы равны.

Объединением множеств А и В называется множество С, если элементы которого принадлежат или А, или В, или обоим множествам, то есть, хотя бы одному из данных множеств

Пересечением множеств А и В называется множество D, состоящее из элементов , одновременно принадлежащих и множеству А и множеству В .

Разностью множеств А и В называется множество Е, состоящее из всех элементов множества А, не принадлежащих множеству В .

Множества, элементами которых являются действительные числа, называются числовыми.

Числовые последовательности.

Числовой последовательностью называется бесконечное множество вещественных чисел, следующих друг за другом и связанных между собой зависимостью от НОМЕРА в последовательности.

Числа называются элементами, или членами последовательности.

- первый член последовательности,

- общий член последовательности.

Последовательность обозначается как .

Например, если дана последовательность , то она имеет вид

, т.к. при

и т.д.

Последовательность можно представить в виде

Последовательность записывается в виде

Общий вид последовательности часто нужно определить по ее общему члену.

Пример. Если последовательность задана как , то общий член равен

Предел последовательности.

Пределом последовательности называется число А, если для любого положительного, сколь угодно малого числа существует такой номер элемента N, что для всех последующих номеров выполняется неравенство

,

то есть все следующие элементы последовательности будут отличаться от предела А на величину, меньшую, чем .

Последовательность, имеющая предел, называется сходящейся.

Предел последовательности обозначается так:

Очевидно, что члены последовательности стремятся к нулю, при (чем на большее число производится деление, тем меньший результат получается),

то есть

Очевидно так же, что последовательности и т.п. тоже имеют предел, равный нулю.

Последовательности, предел которых равен нулю,

называются бесконечно малыми.

Последовательности, не имеющие конечных пределов,

называются бесконечно большими.

Если последовательность - бесконечно малая, то последовательность является бесконечно большой.

Вычисление пределов последовательностей.

*** При вычислении пределов при нужно пользоваться известным пределом бесконечно малых последовательностей и т.п.

Заданные последовательности нужно приводить к бесконечно малым последовательностям - привести возможные элементы числителя и знаменателя последовательности к бесконечно малым вынесением за скобки наибольшей степени многочлена.

Пример 1. Вычислить предел последовательности

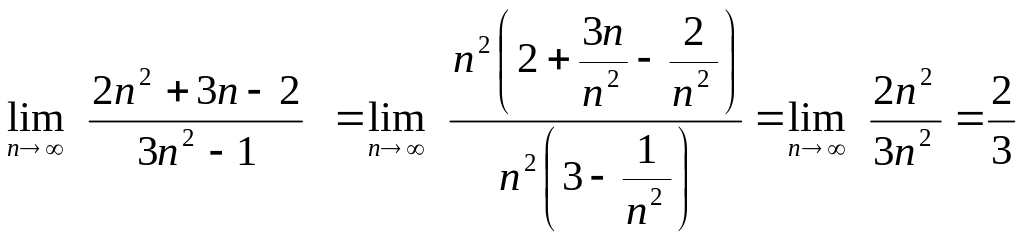
так как

Пример 2. Вычислить предел последовательности

Вынесение наибольшей степени многочлена и приведение к бесконечно малым можно проводить внутри степени (и корня).

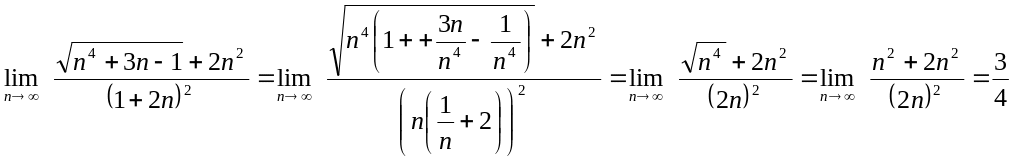
Пример 3. ,

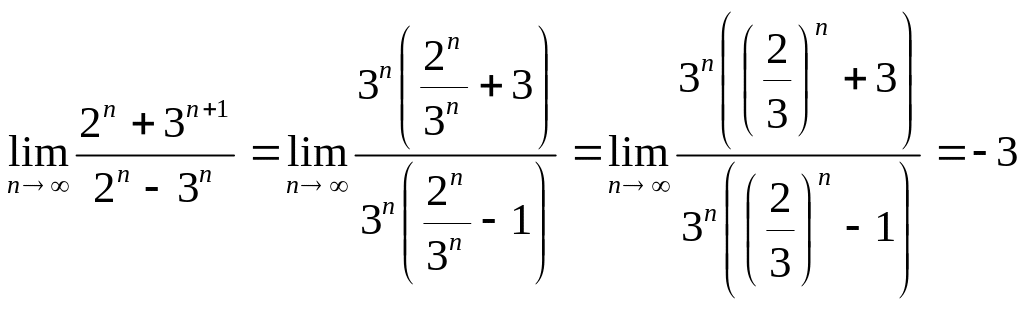потому что функция является убывающей, так как это показательная функция с основанием , то есть . Следовательно,

Пример 4. Вычислить предел последовательности

Предел представляет собой неопределенность .

Для того, чтобы от нее избавиться, нужно произвести избавление от иррациональности.

** Из алгебры известно, что

Если в качестве элементов и используются корни, то формула принимает вид:

Таким образом, чтобы избавить выражение от корня, нужно умножить его на выражение, с аналогичными элементами, но с противоположным знаком. Такое выражение называется сопряженным. Чтобы последовательность не изменилась, нужно на такое же выражение последовательность разделить.

Очевидно, что в числителе можно избавиться от корней и преобразовать полученное выражение

В знаменателе выполняются действия так же, как и в примере 2.

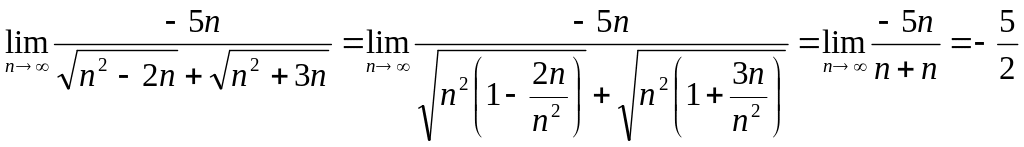
Задания для самостоятельной работы

1. Записать первые пять членов последовательностей:

1) 2) 3) 4) 5)

6) 7) 8)

2. Определить общий член последовательности по ее первым элементам:

1) 2) 3) 4)

3. Вычислить значения пределов последовательностей:

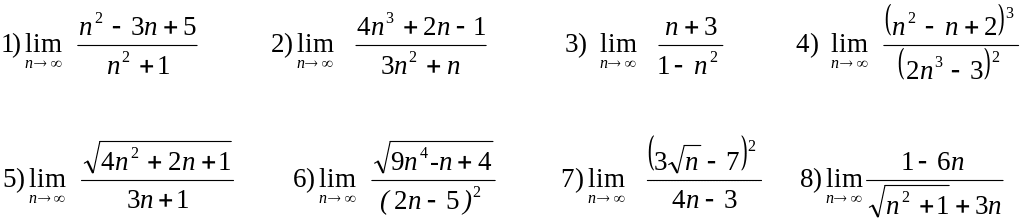
9) 10) 11) 12)

13) 14) 15)

16) 17) 18)

Понятие функции

Есть каждому значению из множества Х ставится в соответствие множество значение из множества У, то задается функция У от Х.

Функцией называется однозначная зависимость переменной У от переменной Х.

При этом переменная Х - независимая переменная и называется аргументом.

!!! В качестве функций могут рассматриваться различные зависимости – зависимость спроса от цены продукции, цены товара от предложения, скорость движения тела от времени, значения давления в газе от температуры и так далее.

Способы задания функции:

• аналитический – представление функции в виде формулы

• табличный – зависимость У от Х задается в виде таблицы значений

• графический – наглядное отображение зависимости У от Х задается в виде графика в системе координат

Предел функции в точке.

Представим функцию в графическом виде

0

слева справа

Рассмотрим последовательность значений , , , предел которой сходится к

значению .

Им соответствуют значения функции, которые тоже составляют последовательность

, сходящуюся к .

Определение предела по Гейне:

Пределом функции в точке

(или пределом функции при ) называется значение А,

если к значению А стремится предел последовательности , элементы которой соответствуют последовательности , пределом которой является значение .

При этом последовательность может стремиться к от меньших значений

при – слева – предел СЛЕВА

И от больших значений - при – справа – предел СПРАВА:

Условие существования предела функции в точке.

Функция имеет предел в точке только тогда, если существуют пределы слева и справа и их значения равны.