Пример минимизации функции. Рассмотрим в качестве примера
функцию четырёх переменных
,
заданную таблицей соответствия
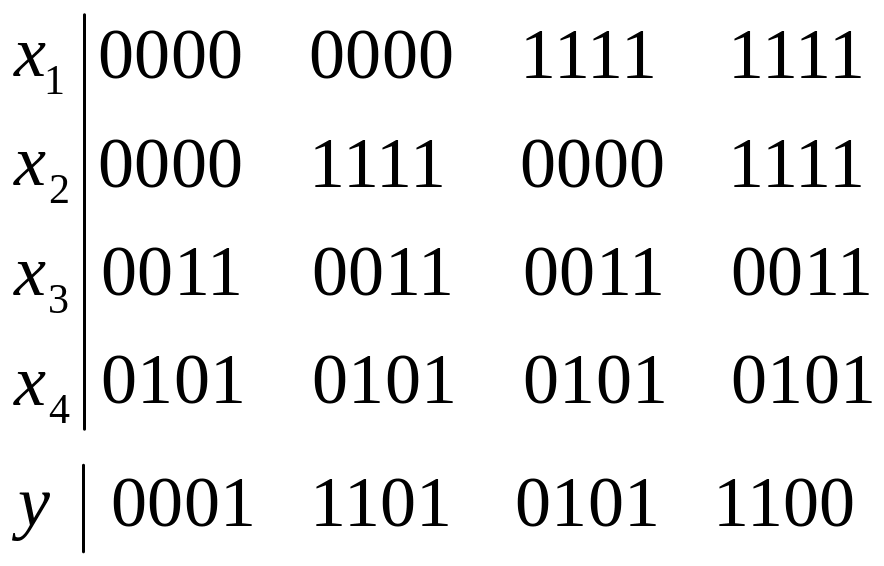
Ей соответствует дизъюнктивная
совершенная нормальная форма
.
Множество 0-кубов после разбиения и
упорядочения записывается следующим
образом:
.
Объединяя и отмечая те из них, которые покрываются кубами большей размерности, имеем:
;
.
Простым импликантам соответствуют не отмеченные кубы. Составляем таблицу покрытия , которому соответствует сокращённая форма
:
|
|
|
|
|
|
|
|
|
Обозначение импликант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Извлекаем единственную
экстремаль
,
которой соответствует минитерм
,
и упрощаем таблицу к виду:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В качестве дополнительных целесообразно
выбрать кубы
и
,
так как они совместно с экстремалью
образуют
покрытие функции, минимальная форма
которой имеет вид:
.
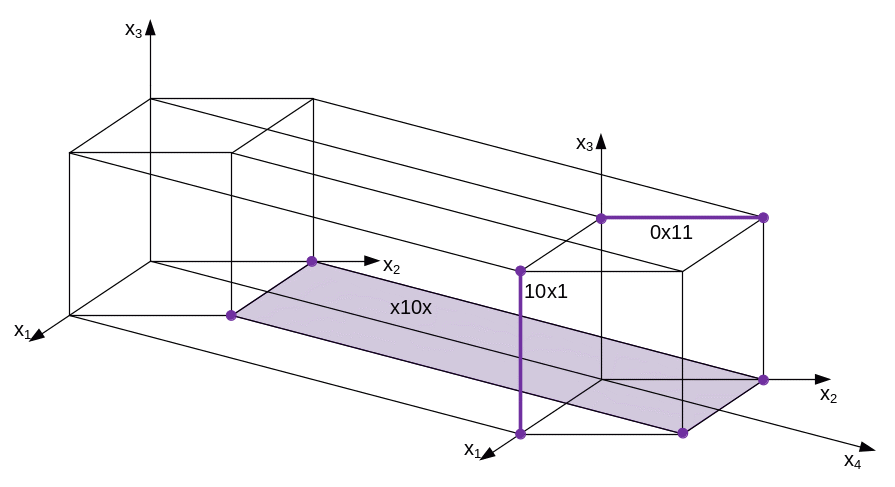
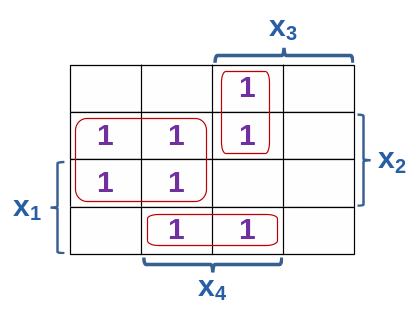
Соответствующее этой функции минимальное
покрытие иллюстрируется на четырёхмерном
кубе и на карте Карно (рис. 226)
|
|
РИСУНОК 226.