2. Применение метода в задаче с ограничениями типа неравенств.

Стратегия поиска решения задачи учитывает тот факт, что решение  может лежать как внутри, так и на границе множества допустимых решений (рис. 4.3 и 4.4).

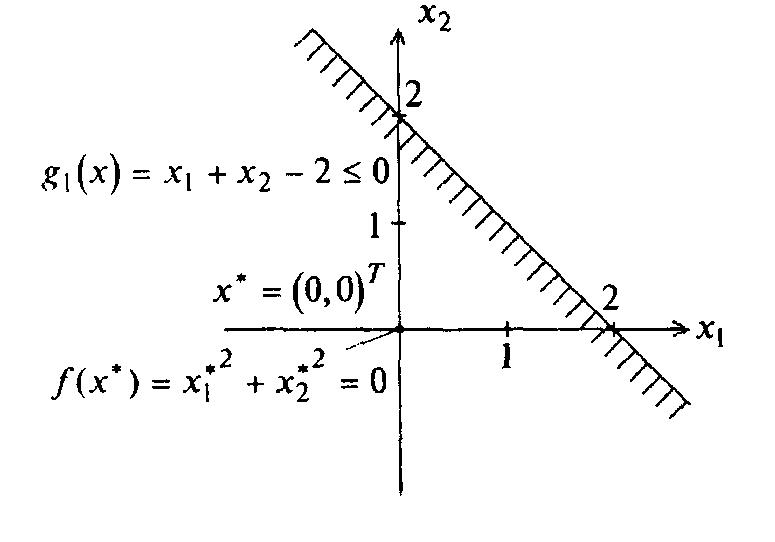
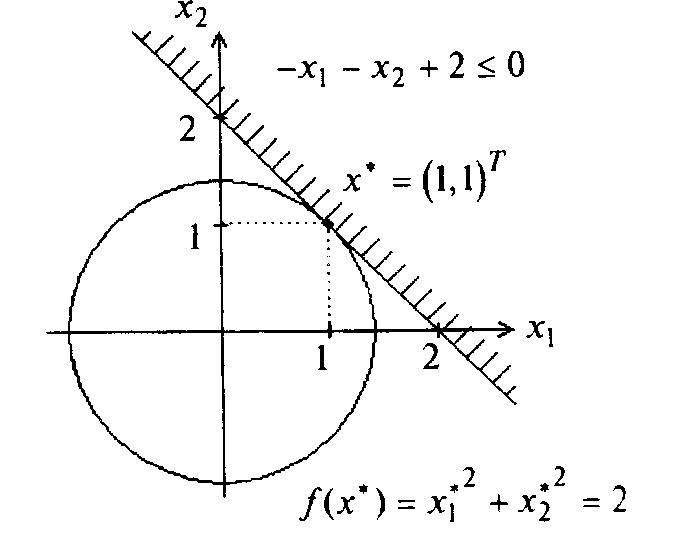
Рисунок 4.3 Рисунок 4.4

Для определения приближения решения  строится последовательность точек , где приращение  определяется в каждой точке  в зависимости от того, где ведётся поиск – внутри или на границе множества допустимых решений.

Решение задачи начинается с обхода границы допустимой области. Обход границ множества допустимых решений связан с выявлением активных в точке  ограничений , аппроксимацией их плоскостью ,

где  - матрица размера , и проекцией на неё вектора . Для выявления неравенств, активных в точке , задаётся погрешность определения активных ограничений . Активными считаются те ограничения, для которых . Число p ограничений, активных в точке , не должно превышать n - размерности вектора x.

Поиск ограничений, активных в точке , рассматривается как самостоятельная задача, которая  может быть решена путём последовательных приближений. Задается точка  и вычисляется . Если , то выбираются любые p ограничений с наименьшими по абсолютной величине невязками  в точке , строится матрица , вычисляется  и находится точка

, (4.2)

затем снова вычисляются невязки выбранных p ограничений. Уточнение по формуле (4.2) осуществляется до тех пор, пока не будет найдена точка , в которой . Проекция вектора  в точке , в которой активны p ограничений, определяется точкой

,

где приращение  осуществляет движение по плоскости  в направлении убывания . Величина выбирается так: , где  есть шаг, при котором

,

а  - наименьший шаг, при котором

для всех ограничений, которые не были активными в точке . Разумеется, невязка ограничений в точке  изменяется, и поэтому вычислению точки  должна предшествовать процедура выбора активных ограничений, описанная выше.

Процедура вычисления точек последовательности  обеспечивает последовательное движение вдоль границы допустимой области. При выполнении неравенства , где  - заданное достаточно малое положительное число, вычисляется приближение  вектора множителей Лагранжа :

.

Если , то в точке  выполнены необходимые условия минимума и в ней должны быть проверены достаточные условия. Если среди множителей  есть отрицательные, то это означает, что  не является приближением точки , так как в ней не выполнены необходимые условия минимума  при ограничениях . Однако выбор шага  позволяет говорить о том, что значение  не может быть уменьшено при заданном составе активных ограничений и, следовательно, процесс минимизации  необходимо продолжить, уменьшив их число: в число пассивных переводится то из ограничений, которому соответствует наибольший по абсолютному значению отрицательный множитель . Такая процедура поиска позволяет отыскать решение, лежащее как на границе, так и внутри множества допустимых решений.

Алгоритм:

Шаг 1. Задать начальную точку число итераций M.

Шаг 2. Положить k=0.

Шаг 3. Проверить условие :

а) если неравенство выполняется, то расчет окончен. Вычислить , проверить необходимые и достаточные условия минимума и оценить результат;

б) если нет, перейти к шагу 4.

Шаг 4.Вычислить .

Шаг 5. Проверить выполнение условий :

а) если неравенство выполнено хотя бы для одного j, вычислить . Если , перейти к шагу 7. Если при k > 0, перейти к шагу 9, а если , то следует проверить точку на принадлежность области допустимых решений. Если , перейти к шагу 9. В противном случае задать заново точку и перейти к шагу 4.

б) если ни одно из условий не выполнено, перейти к шагу 6.

Шаг 6. Вычислить точку , в которой будет выполнено условие , по крайней мере для одного значения . Положить и перейти к шагу 7.

Шаг 7. Вычислить .

Шаг 8. Проверить условие :

а) если неравенство выполняется, перейти к шагу 9;

б) если нет – к шагу 10.

Шаг 9. Вычислить вектор . Если , то расчет окончен, проверить достаточные условия минимума. Если нет, то исключить из состава активных ограничение (оно переводится в пассивные), которому соответствует наибольший по модулю отрицательный множитель, и перейти к шагу 7 (при этом из матрицы удаляется строка, соответствующая исключаемому ограничению).

Шаг 10. Получить точку .

Шаг 11. Определить . Для этого следует:

а) вычислить из условия ;

б) для всех пассивных в точке ограничений, кроме переведенных в пассивные на шаге 9, определить величину из условия (если условие выполняется только при , то не вычисляется);

в) найти величину ;

г) вычислить значение .

Шаг 12. Вычислить . Положить и перейти к шагу 3.

Пример: Найти минимум в задаче

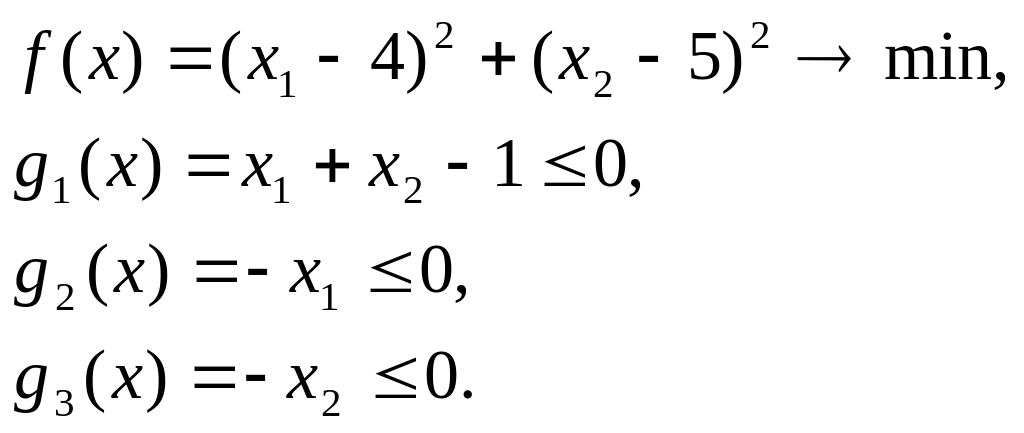
Решение:

1. Зададим , M =5.

2. Положим k = 0.

3⁰. Проверим условие : .

4⁰. Вычисляем .

5⁰. В точке активны ограничения , они формируют матрицу . Т.к. , переходим к шагу 7.

7⁰. Вычисляем , т.к. .

8⁰. Проверяем условие: , переходим к шагу 9.

9⁰. Вычисляем , удаляем третье ограничение (оно переходит в пассивные), которому соответствует наибольший по модулю отрицательный множитель -10, и переходим к шагу 7 (при этом исключается вторая строка из матрицы ).

7¹. Вычисляем , т.к. .

8¹. Проверяем условие: .

10⁰. Получаем точку .

11⁰. Определяем : величину находим из условия: ; т.к. первое ограничение пассивно в точке , то из условий и находим ; третье ограничение в аналогичной процедуре не участвует, поскольку переведено в пассивные только на шаге 9; .

12⁰. Вычисляем (см. рисунок 4.5). Полагаем и переходим к шагу 3.

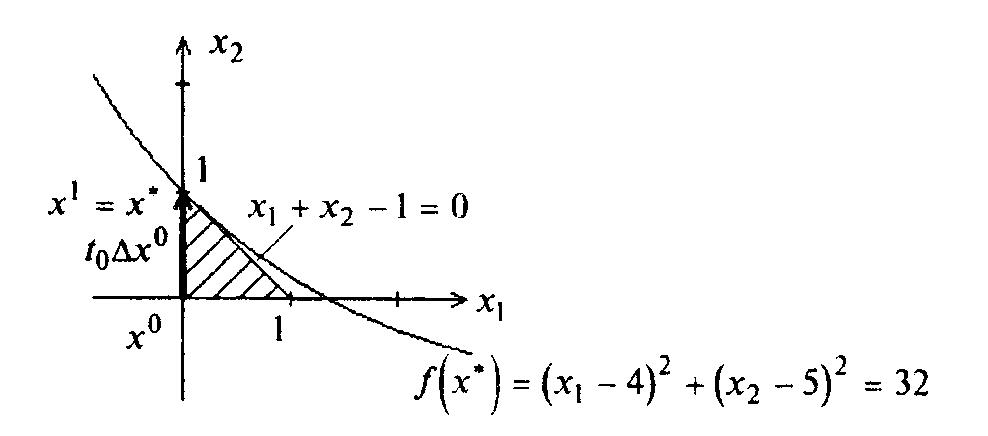
Рисунок 4.5

3¹. Проверим условие : .

4¹. Вычисляем .

5¹. Проверяем условия .

Активны первое и второе ограничения, они формируют матрицу , .

7¹. Вычисляем , т.к. .

8¹. Проверяем условие: , переходим к шагу 9.

9⁰. Вычисляем . Необходимые условия выполнены.

Проверяем достаточные условия минимума: . Дополнительные условия . Отсюда . Следовательно, . Точка - точка минимума .