3.3 Комбинированный метод штрафных функций
Для ограничений типа равенств применяется метод штрафов (внешних штрафов), а для ограничений-неравенств – метод барьерных функций (внутренних штрафов).
Задача на условный минимум сводится к решению последовательности задач поиска минимума смешанной вспомогательной функции:
или
,
где - параметр штрафа.
Начальная
точка задаётся так, чтобы
ограничения-неравенства строго
выполнялись:
.
На каждой k-й
итерации ищется точка
минимума
смешанной вспомогательной функции при
заданном параметре
с
помощью одного из методов безусловной
минимизации. Полученная точка
используется
в качестве начальной на следующей
итерации, выполняемой при уменьшающемся
значении параметра штрафа. При
последовательность
точек
стремится
к точке условного минимума
.
Алгоритм:
Шаг
1. Задать
начальную точку
так,
чтобы
;
начальное значение параметра штрафа
;
число
для уменьшения параметра штрафа; малое
число
для
остановки алгоритма. Положить
.
Шаг 2. Составить смешанную вспомогательную функцию
или
.
Шаг 3. Найти точку минимума функции с помощью какого-либо метода поиска безусловного минимума с проверкой выполнения справедливости неравенств: . При этом задать все требуемые выбранным методом параметры. В качестве начальной точки взять .
Шаг 4. Вычислить и проверить условие окончания:
a) если , процесс поиска закончить:
;
b)
если
,
положить
и
перейти к шагу 2.
Замечания:
а)
Метод предложен Фиакко А. и Мак-Кормиком
Г. Они рекомендуют
.
б) Можно использовать разные параметры штрафа для внешних и внутренних штрафов.
в) Для данного метода справедливы замечания для методов штрафа и барьерных функций.
г) Побочным продуктом вычислений является вектор множителей Лагранжа:
;
-
для обратной штрафной функции;
-
для логарифмической штрафной функции;
.
Пример: Найти минимум в задаче
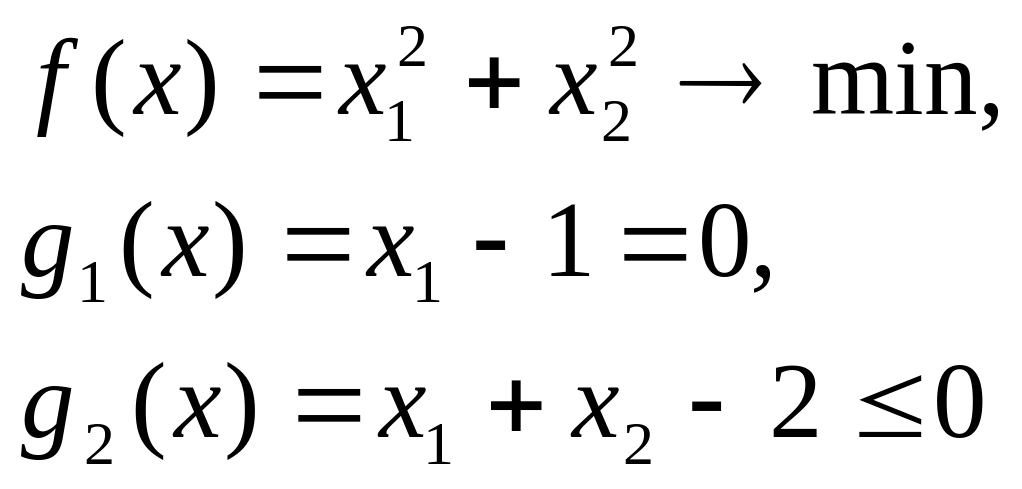
Решение:
1.
В поставленной задаче
.
Решим ее аналитически. Положим
.
2. Составим смешанную вспомогательную штрафную функцию:
.
3. Найдем безусловный минимум с помощью необходимых условий экстремума первого порядка:
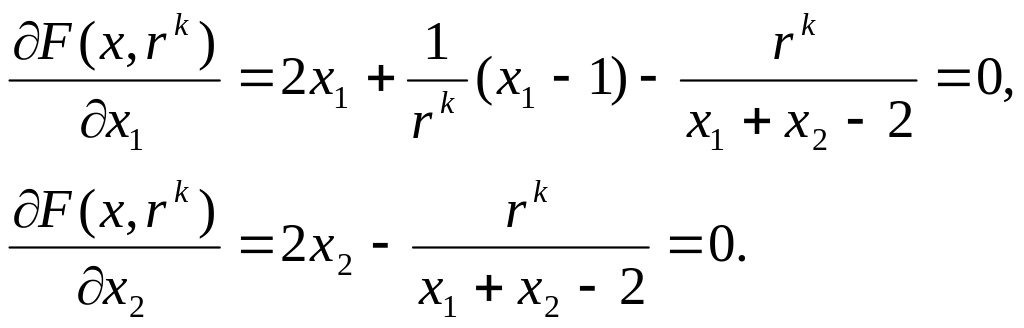
Вычитая,
имеем
,
а
находится в результате решения уравнения
.
При
имеем
или
.
Отсюда получаем
Для
первой пары корней имеем
,
т.е. они не лежат в допустимой области.
Поэтому
.
При
имеем
или
.
Отсюда получаем
Первая
пара корней не лежит в допустимой
области. Поэтому
.
При
имеем
или
.
Отсюда получаем
Первая
пара корней не лежит в допустимой
области. Поэтому
.
При
имеем
или
.
Отсюда получаем
Первая
пара корней не лежит в допустимой
области. Поэтому
.
При
имеем
или
.
Отсюда получаем
Первая
пара корней не лежит в допустимой
области. Поэтому
.
Т.к.
в полученной точке
,
то расчет завершается:
.
Легко показать, что достаточные условия безусловного минимума функции во всех найденных точках удовлетворяются. Оценки множителей Лагранжа легко вычисляются по формулам:
;
.
Результаты расчетов приведены в таблице:
k |
|
|
|
|
|
|
0 |
1 |
0,1722 |
-0,2416 |
-0,3846 |
-0,8278 |
0,483 |
1 |
|
0,6378 |
-0,0866 |
0,16969 |
-1,4488 |
0,1725 |
2 |
|
0,8858 |
-0,0273 |
0,095 |
-1,8272 |
0,0547 |
3 |
|
0,9694 |
-0,00756 |
0,0299 |
-1,9584 |
0,01505 |
4 |
|
0,99223 |
-0,00198 |
0,00768 |
-1,9891 |
0,0038 |
Графическая иллюстрация дана на рисунке 3.5.
Рисунок 3.5