4 Методы возможных направлений

4.1 Метод проекции градиента (метод Розена)

1. Применение метода в задаче с ограничениями типа равенств.

Стратегия поиска решения задачи методом проекции градиента состоит в построении последовательности точек , вычисляемых по правилу

,

где  есть вектор, вычисляемый для каждого значения k. Приращение  определяется из условия проекции вектора , на аппроксимирующую плоскость, задаваемую уравнением

,

которая аппроксимирует в точке , поверхность Г, задаваемую уравнениями . Здесь  - матрица размера  вида

,

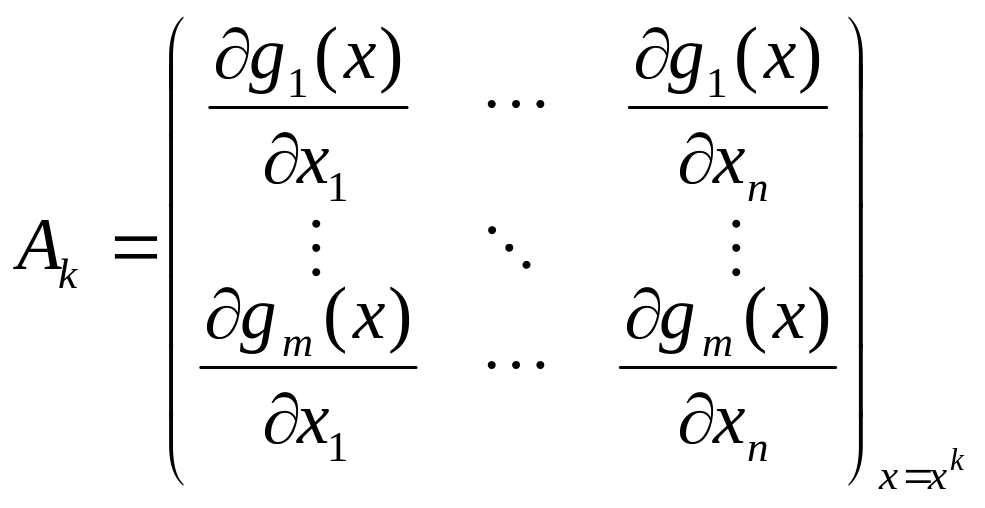а  - вектор столбец, .

На рисунке 4.1 в точке  построена аппроксимирующая прямая для задачи .

Её уравнение , т.к ;   и, следовательно, .

Вектор  определяется по формуле

,

где  называется градиентной составляющей приращения; она равна

и обладает следующим свойством: градиентная составляющая приращения  в линейном приближении не меняет вектор невязки условий связи. Это означает, что под действием градиентной составляющей точка  движется параллельно или по плоскости  (рисунок 4.1). Составляющая  называется компенсационной составляющей приращения и равна . Эта составляющая обладает, в линейном приближении, свойством компенсировать вектор невязки условий связи на величину . Под действием составляющей  осуществляется проекция точки  на плоскость  (рисунок 4.1).

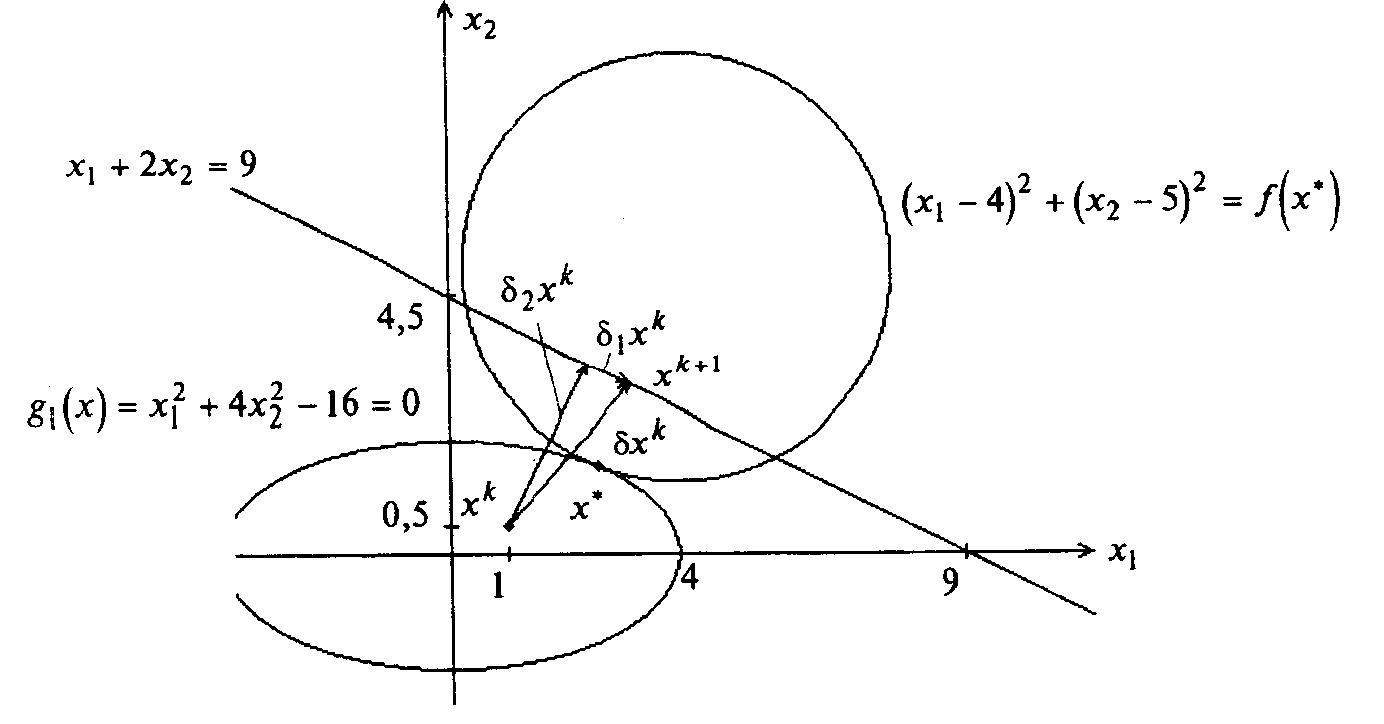
Рисунок 4.1

Величина шага  может выбираться как из условия убывания  при переходе из точки  в точку , так и из условия

. (4.1)

Задача (4.1) может решаться либо с использованием необходимых и достаточных условий минимума: , применяемых непосредственно к функции  или к аппроксимирующим её полиномам, либо с использованием численных методов.

Расчёт заканчивается в точке , в которой , , где  - заданное число. В полученной точке  требуется обязательная проверка выполнения достаточных условий минимума функции в исходной задаче. Точное равенство  свидетельствует о точном выполнении необходимых условий экстремума, при этом вектор множителей Лагранжа определяется по формуле

.

Знание приближения  вектора   позволит осуществить проверку достаточных условий в точке .

Замечание:

Если в исходной задаче ограничения линейны, т.е. имеют вид , то матрица A постоянна. Это означает, что в силу свойства компенсационной составляющей она вычисляется единственный раз в точке . При этом начальная точка попадает в область допустимых решений за одну итерацию. Дальнейший процесс построения последовательности связан с вычислением составляющей .

Алгоритм:

Шаг 1. Задать начальную точку число итераций M.

Шаг 2. Положить k=0.

Шаг 3. Проверить условие :

а) если неравенство выполняется, то расчет окончен. Вычислить , проверить необходимые и достаточные условия минимума и оценить результат;

б) если нет, перейти к шагу 4.

Шаг 4.Вычислить матрицу

.

Шаг 5. Вычислить .

Шаг 6. Вычислить .

Шаг 7. Вычислить .

Шаг 8. Вычислить .

Шаг 9. Вычислить .

Шаг 10. Проверить выполнение условий :

а) если , то расчет окончен. Вычислить , проверить необходимые и достаточные условия минимума и оценить результат;

б) если , то положить и перейти к шагу 11.

в) если , то положить и перейти к шагу 13.

г) если , то перейти к шагу 11.

Шаг 11. Получить точку .

Шаг 12. Определить из условия .

Шаг 13. Вычислить . Положить и перейти к шагу 3.

Замечание:

Если ограничения в задаче линейны, то при на шаге 3 переходим к шагу 8. На шаге 10 следует положить .

Пример: Найти минимум в задаче

Решение:

Ограничение в задаче является линейным (см. рисунок 4.2).

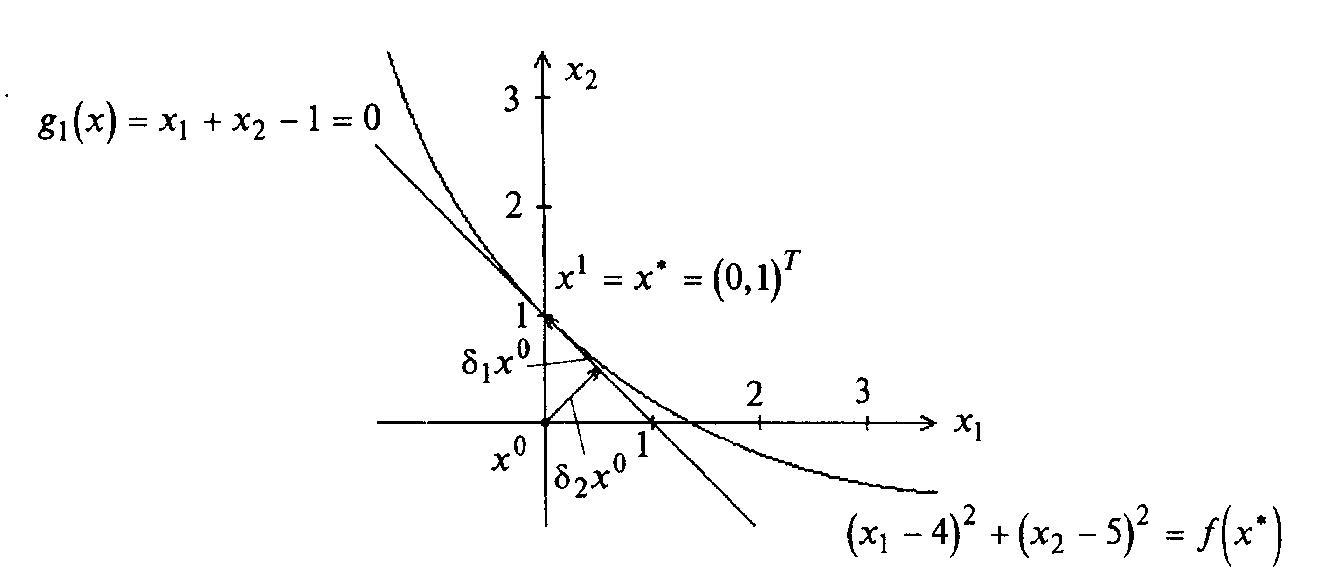
Рисунок 4.2

1. Зададим , M =5.

2. Положим k = 0.

3⁰. Проверим условие : .

4⁰.Вычисляем матрицу .

5⁰. Вычислим .

6⁰. Находим .

7⁰. Вычисляем .

8⁰. Вычислим : .

9⁰. Вычисляем .

10⁰. Проверяем выполнение условий: :

. Переходим к шагу 11.

11⁰. Получаем точку .

12⁰. Определяем из условия: .

13⁰. Вычисляем . Полагаем и переходим к шагу 3.

3¹. Проверим условие : .

8¹. Вычислим : .

9¹. Вычисляем .

10¹. Проверяем выполнение условий: :

. Расчет окончен. Вычисляем множитель Лагранжа

. Проверяем достаточные условия минимума. Второй дифференциал функции Лагранжа равен . Дополнительное условие: , откуда . Подставляя в , имеем . Вывод: точка - точка минимума.