
- •Киров 2006
- •Рецензент: к.Т.Н., доцент каф. Эвм Матвеева л.И.
- •1 Оформление лабораторной работы
- •1.1 Цель работы
- •1.2 Формирование отчета
- •2 Общие принципы методов поиска условного экстремума
- •3 Методы последовательной безусловной минимизации
- •3.1 Метод штрафов
- •3.2 Метод барьерных функций
- •1) Применение обратной штрафной функции
- •2) Применение логарифмической штрафной функции
- •3.3 Комбинированный метод штрафных функций
- •3.4 Метод множителей
- •3.5 Метод точных штрафных функций
- •4 Методы возможных направлений
- •4.1 Метод проекции градиента (метод Розена)
- •1. Применение метода в задаче с ограничениями типа равенств.
- •2. Применение метода в задаче с ограничениями типа неравенств.
- •4.2 Метод Зойтендейка
- •5 Пример отчета по лабораторной работе
- •6 Блок вариантов заданий
- •7 Библиографический список
3.4 Метод множителей
Стратегия аналогична используемой в методе внешних штрафов, только штрафная функция добавляется не к целевой функции, а к классической функции Лагранжа. В результате задача на условный минимум сводится к решению последовательности задач поиска безусловного минимума модифицированной функции Лагранжа:
![]() ,
где
,
где
![]() -
векторы множителей;
-
параметр штрафа; k -
номер итерации.
-
векторы множителей;
-
параметр штрафа; k -
номер итерации.
Задается
начальная точка поиска
.
На каждой
-й
итерации ищется точка минимума
модифицированной функции Лагранжа при
заданных
![]() с помощью одного
из методов безусловной минимизации.
Полученная точка
с помощью одного
из методов безусловной минимизации.
Полученная точка
![]() используется
в качестве начальной на следующей
итерации, выполняемой при возрастающем
значении параметра штрафа
и
пересчитанных определённым образом
векторах множителей
используется
в качестве начальной на следующей
итерации, выполняемой при возрастающем
значении параметра штрафа
и
пересчитанных определённым образом
векторах множителей
![]() .
Для достижения сходимости в отличие от
метода внешних штрафов не требуется
устремлять
к
бесконечности.
.
Для достижения сходимости в отличие от
метода внешних штрафов не требуется
устремлять
к
бесконечности.
Алгоритм:
Шаг 1. Задать начальную точку ; начальное значение параметра штрафа ; число для увеличения параметра; Начальные значения векторов множителей ; малое число для остановки алгоритма. Положить .
Шаг 2. Составить модифицированную функцию Лагранжа:
.
Шаг 3. Найти точку безусловного минимума функции по x с помощью какого-либо метода (нулевого, первого или второго порядка):
![]() .
.
При
этом задать все требуемые выбранным
методом параметры. В качестве начальной
точки взять
![]() .
.
Шаг
4. Вычислить
![]() ,
,
где
![]() и проверить выполнение условия окончания:
и проверить выполнение условия окончания:
a)
если
![]() ,
процесс поиска закончить:
,
процесс поиска закончить:
![]() ;
;
b)
если
![]() ,
положить:
,
положить:
![]() (пересчёт
параметра штрафа);
(пересчёт
параметра штрафа);
![]() (пересчёт
множителей для ограничений-равенств);
(пересчёт
множителей для ограничений-равенств);
![]() (пересчёт
множителей для ограничений-неравенств);
(пересчёт
множителей для ограничений-неравенств);
![]() ,
и перейти к шагу 2.
,
и перейти к шагу 2.
Утверждение
3 (о сходимости метода множителей в
задаче с ограничениями типа равенств)
Пусть функции
![]() непрерывны, последовательность
непрерывны, последовательность
![]() ограничена,
ограничена,
![]() при всех k,
причем
,
- компактное изолированное множество
точек локального минимума в исходной
задаче. Тогда найдется подпоследовательность
при всех k,
причем
,
- компактное изолированное множество
точек локального минимума в исходной
задаче. Тогда найдется подпоследовательность
![]() ,
сходящаяся к некоторой точке
,
сходящаяся к некоторой точке
![]() и такая, что ее произвольный элемент
и такая, что ее произвольный элемент
![]() является точкой локального минимума
функции
является точкой локального минимума
функции
![]() .
Если при этом
состоит из единственной точки
,
то можно указать последовательность
.
Если при этом
состоит из единственной точки
,
то можно указать последовательность
![]() и номер
и номер
![]() такие, что
такие, что
![]() и
и
![]() является точкой локального минимума
функции
при
является точкой локального минимума
функции
при
![]() .
.
Замечания:
а) На каждой итерации желательно, чтобы найденная точка локального минимума была бы ближайшей к . Метод корректен, если начиная с некоторого k метод безусловной минимизации всякий раз приводит в окрестность одной и той же точки условного локального минимума.
б)
Если
![]() ,
то через конечное число итераций те
множители, которые соответствуют
ограничениям, не являющимся активными
в точке
,
обратятся в нуль.
,
то через конечное число итераций те
множители, которые соответствуют
ограничениям, не являющимся активными
в точке
,
обратятся в нуль.
в)
Обычно
![]() .
Целесообразно выбрать
.
Целесообразно выбрать
![]() близкими к
близкими к
![]() ,
используя априорную информацию о
решении. Иногда выбирают
,
используя априорную информацию о
решении. Иногда выбирают
![]() .
В этом случае первая вспомогательная
задача минимизации совпадает с решаемой
в методе внешних штрафов.
.
В этом случае первая вспомогательная
задача минимизации совпадает с решаемой
в методе внешних штрафов.
г) Методом множителей удается найти условный минимум за меньшее число итераций, чем методом штрафов. При этом для достижения сходимости не требуется устремлять к бесконечности. Доказано, что минимум модифицированной функции Лагранжа, начиная с некоторого , совпадает с минимумом в исходной задаче. Это приводит также к тому, что проблема увеличения овражности не является такой острой, как в методе штрафов.
д) Метод множителей был предложен Пауэллом и Хестенсом и имеет многочисленные модификации.
Пример: Найти минимум в задаче
Решение:
1.
В поставленной задаче
![]() .
Решим ее аналитически. Положим
.
Решим ее аналитически. Положим
![]() .
Выберем для сравнения последовательность
,
используемую в примере в методе штрафов.
.
Выберем для сравнения последовательность
,
используемую в примере в методе штрафов.
2. Составим модифицированную функцию Лагранжа:
![]()
3.
Найдем безусловный минимум
![]() при фиксированных
при фиксированных
![]() :
:
![]()
Во
втором случае
.
Но при
![]() всегда выполняется
всегда выполняется
![]() ,
т.к.
,
т.к.
![]() в силу шага 4 алгоритма здесь не изменяется.
Поэтому найденная точка не является
решением.
в силу шага 4 алгоритма здесь не изменяется.
Поэтому найденная точка не является
решением.
В
первом случае имеем
![]() .
.
Кроме
того,
![]() ,
т.е. достаточные условия минимума
выполняются. Проведем расчеты при
различных k.
,
т.е. достаточные условия минимума
выполняются. Проведем расчеты при
различных k.
При
получаем
![]() .
.
Имеем
![]() ,
поэтому
,
поэтому
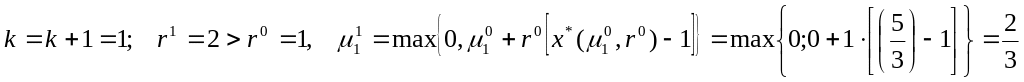 .
.
При
![]() получаем
получаем
![]() .
.
Имеем
![]() ,
поэтому
,
поэтому
![]() .
.
При
![]() получаем
получаем
![]() .
.
Имеем
![]() ,
поэтому
,
поэтому
![]() .
.
При
![]() получаем
получаем
![]() .
.
Имеем
![]() ,
поэтому
,
поэтому
![]() .
.
При
![]() получаем
получаем
![]() .
.
Имеем
![]() ,
поэтому процесс завершается:
,
поэтому процесс завершается:
![]() .
.
Результаты расчетов приведены в таблице:
k |
|
|
|
|
|
|
0 |
1 |
0 |
|
-3,66 |
|
0,222 |
1 |
2 |
|
1,333 |
-3,2218 |
0,333 |
0,333 |
2 |
10 |
1,333 |
1,0555 |
-3,100 |
0,0555 |
0,0075 |
3 |
100 |
1,888 |
1,00109 |
-3,00006 |
0,00109 |
0,0021 |
4 |
1000 |
1,997 |
1,0000029 |
-3,00000 |
0,0000029 |
0,0000058 |
