1) Применение обратной штрафной функции
1.
В поставленной задаче
.
Решим ее аналитически.
2. Составим вспомогательную штрафную функцию:
.
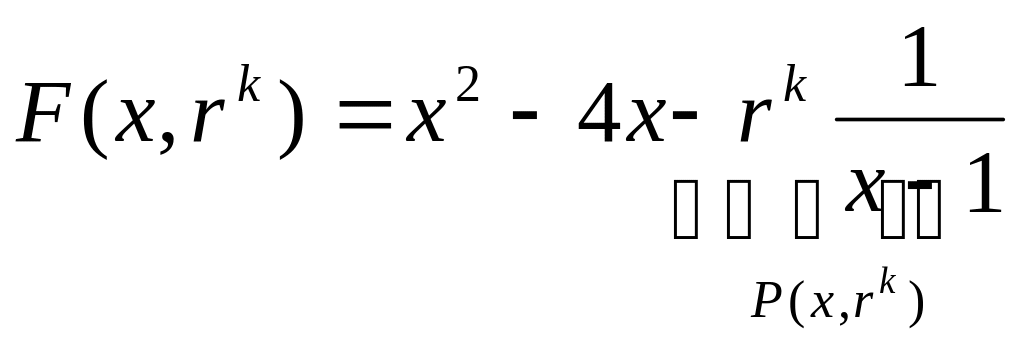3. Найдем минимум с помощью необходимых и достаточных условий:
.
Т.к.
рассматривается внутренность множества
X,
то
,
а уравнение для нахождения стационарных
точек имеет вид:
.
Найдем
корни по формуле Кардана. Уравнение,
представленное в канонической форме
,
запишем в виде
,
поделив на a
и введя вместо x
новую переменную
.
При этом
.
Т.к.
,
то
и
и, следовательно
.
Дискриминант
.
Если D
> 0, уравнение
имеет один действительный корень; если
D
< 0, уравнение
имеет три различных корня; если D
= 0, уравнение
имеет одно решение при
(три совпадающих нулевых корня) и два
решения при
(из трех действительных - два совпали).
При
имеем D
> 0, а при
получаем D
< 0. Искомые
корни находятся по формулам:
где
.
При
и
можно найти
,
знак r
совпадает
со знаком q.
Находится вспомогательная величина
,
а затем
.
Положим
.
Тогда справедливы равенства:
Пусть
.
Тогда
Т.к.
и
,
то:
.
Тогда
.
Корни
и
не лежат внутри допустимой области.
Поэтому
.
Пусть
.
Тогда
Т.к.
и
,
то:
.
Тогда
.
Корни
и
не лежат внутри допустимой области.
Поэтому
.
Пусть
.
Тогда
Т.к.
и
,
то:
.
Тогда
.
Корни
и
не лежат внутри допустимой области.
Поэтому
.
Видно,
что при
.
Кроме того, во всех точках
,
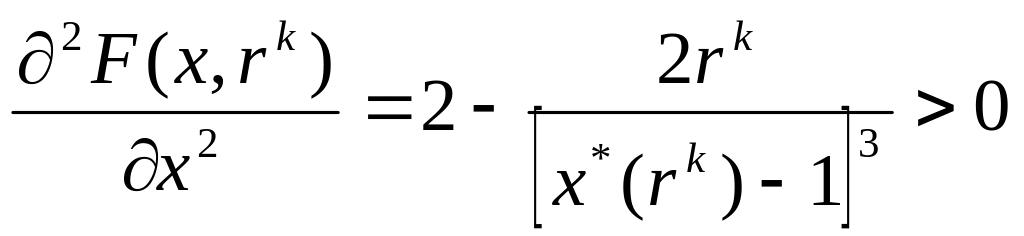т.е. достаточное условие безусловного минимума выполняется. Согласно п. д) замечаний найдем оценки множителя Лагранжа:
.
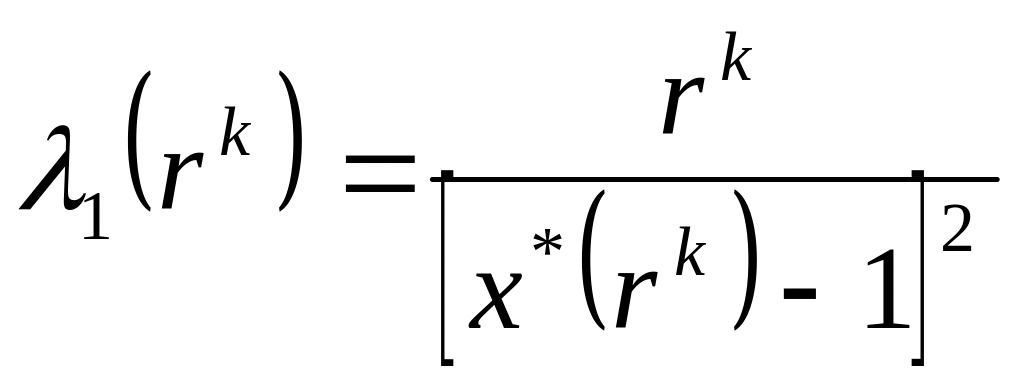При
.
Очевидно,
при
.
Результаты расчетов приведены в таблице:
k |
|
|
|
|
|
0 |
1 |
0,435 |
0,219 |
1,77 |
3,13 |
1 |
0,1 |
0,798 |
-2,06 |
0,495 |
2,45 |
2 |
0,01 |
0,932 |
-2,712 |
0,147 |
2,16 |
3 |
0,001 |
0,978 |
-2,91 |
0,045 |
2,066 |
4 |
0 |
1 |
-3 |
- |
2 |
Графическая иллюстрация дана на рисунке 3.4.
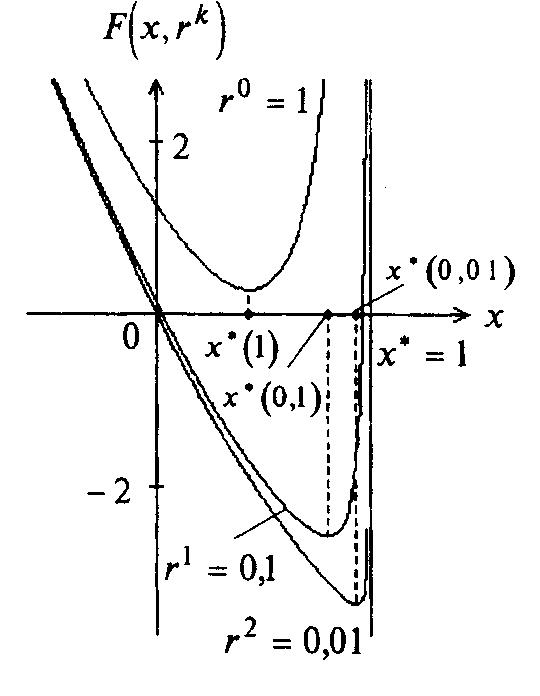
Рисунок 3.4
2) Применение логарифмической штрафной функции
1. В поставленной задаче . Решим ее аналитически.
2. Составим вспомогательную штрафную функцию:
.
3. Найдем минимум с помощью необходимых и достаточных условий:
.
Т.к.
рассматривается внутренность множества
X,
то
.
Отсюда получаем уравнение
.
Его решения имеют вид
.
Корень
не лежит в области X,
поэтому
.
Во всех точках
,
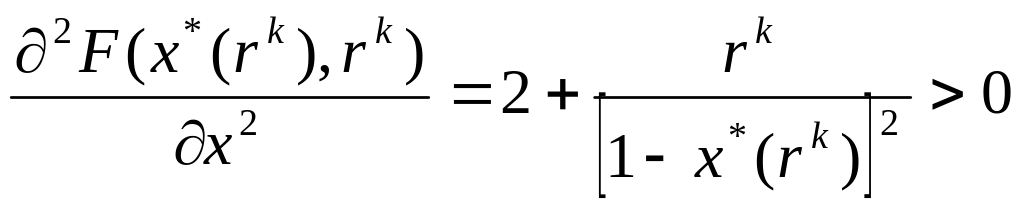т.е. достаточное условие безусловного минимума выполняется.
Результаты расчетов приведены в таблице:
k |
|
|
|
|
|
0 |
1 |
0,634 |
-1,13 |
1,005 |
2,73 |
1 |
0,1 |
0,952 |
-2,59 |
0,303 |
2,08 |
2 |
0,01 |
0,995 |
-2,937 |
0,053 |
2 |
3 |
0,001 |
0,9995 |
-2,99 |
0,0076 |
2 |
4 |
0 |
1 |
-3 |
- |
2 |
