3.2 Метод барьерных функций
Идея
метода заключается в сведении задачи
на условный минимум к решению
последовательности задач поиска минимума
вспомогательной
функции
,
где
-
штрафная функция,
-
параметр штрафа.
Как правило, используются:
обратная штрафная функция
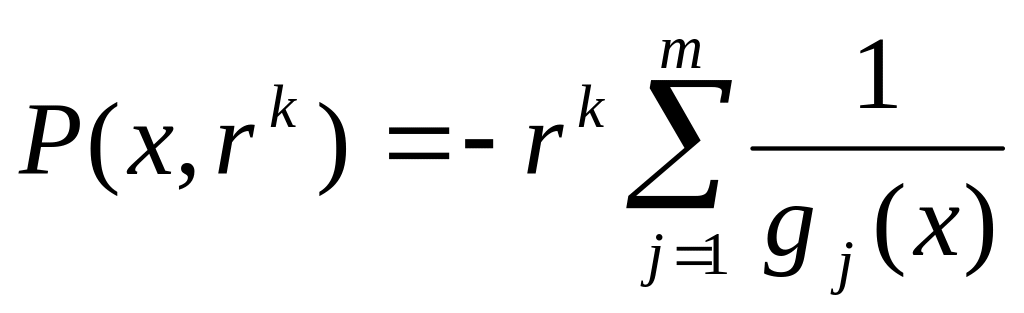(см. рисунок 3.2);
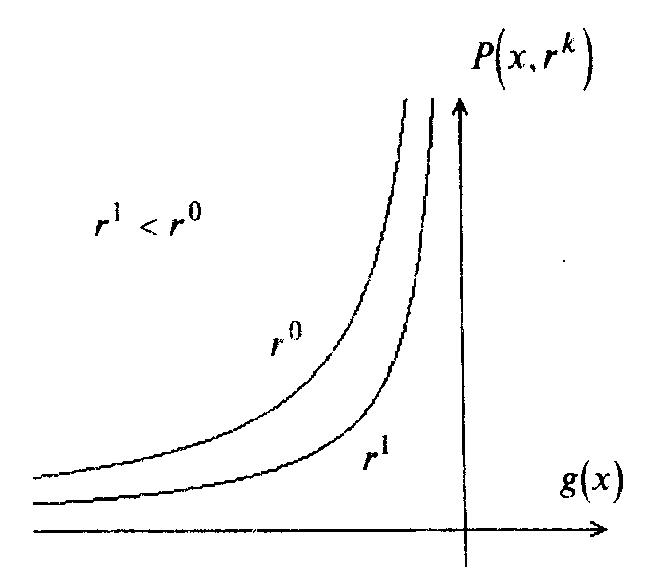
Рисунок 3.2
b)
логарифмическая штрафная функция
(см. рисунок 3.3).
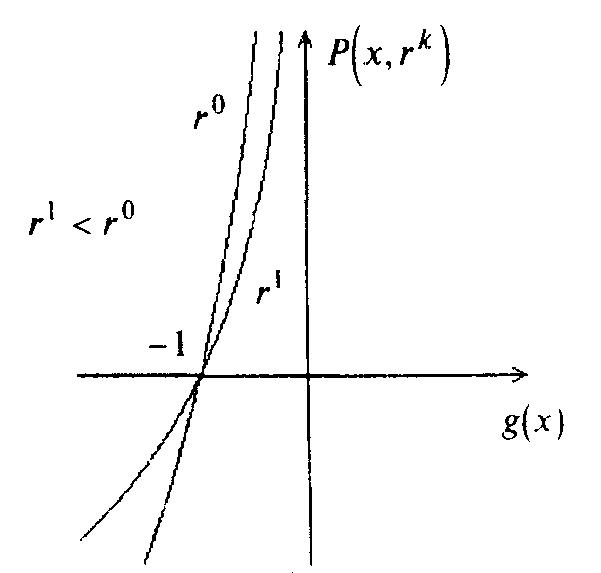
Рисунок 3.3
Обе
штрафные функции определены и непрерывны
внутри множества X,
т.е. на множестве
,
и стремятся к бесконечности при
приближении к границе множества изнутри.
Поэтому они называются барьерными
функциями. При
штрафная
функция, задаваемая обратной функцией,
положительна. Логарифмическая штрафная
функция положительна при
и
отрицательна при
,
т.е. внутренним точкам области отдаётся
предпочтение перед граничными точками.
Начальная
точка задаётся только внутри множества
X.
На каждой k-й
итерации ищется точка
минимума
вспомогательной функции
при
заданном параметре
с
помощью одного из методов безусловной
минимизации. Полученная точка
используется
в качестве начальной на следующей
итерации, выполняемой при уменьшающемся
значении параметра штрафа. При
последовательность
точек
стремится
к точке условного минимума
.
Барьерные функции как бы препятствуют
выходу из множества X,
а если решение задачи лежит на границе,
то процедура метода приводит к движению
изнутри области к границе.
Согласно описанной процедуре точки лежат внутри множества допустимых решений для каждого . Этим объясняется то, что метод барьерных функций иногда называется методом внутренних штрафов.
Алгоритм:
Шаг
1. Задать
начальную точку
внутри
области X;
начальное значение параметра штрафа
;
число
для
уменьшения параметра штрафа; малое
число
для
остановки алгоритма. Положить
.
Шаг 2. Составить вспомогательную функцию:
или
.
Шаг 3. Найти точку минимума функции с помощью какого-либо метода (нулевого, первого или второго порядка) поиска безусловного минимума с проверкой принадлежности текущей точки внутренности множества X. При этом задать все требуемые выбранным методом параметры. В качестве начальной точки взять . Вычислить:
или
.
Шаг 4. Проверить выполнение условия окончания:
a)
если
,
процесс поиска закончить:
;
b)
если
,
положить
и перейти к шагу 2.
Утверждение
2 Пусть
функции
,
выпуклы и конечны, множество
решений
задачи поиска условно минимума не пусто
и ограничено, существует точка
такая, что 
.
Тогда в методе барьерных функций
,
функции
выпуклы,
последовательность
,
порожденная алгоритмом, ограничена и
все ее предельные точки принадлежат
,
причем
.
Замечания:
а)
Обычно выбирается
,
а
.
б) При обеспечивается сходимость, однако с уменьшением функция становится все более овражной. Поэтому полагать малым числом сразу нецелесообразно.
в) Обратная штрафная функция была предложена Кэрроллом, а логарифмическая Фришем.
г) Т.к. большинство методов поиска безусловного экстремума использует дискретные шаги, то вблизи границы шаг может привести в точку вне допустимой области. Если в алгоритме отсутствует проверка на принадлежность точки множеству , это может привести у ложному успеху, т.е. уменьшению вспомогательной функции в точке, где она теоретически неопределена. Поэтому на шаге 3 алгоритма требуется явная проверка того, что точка не покинула допустимую область. Процедура поиска обычно завершается при некотором малом , отличном от нуля. Однако приближенное решение принадлежит множеству допустимых решений. Это одно из преимуществ метода барьерных функций.
д) Побочным продуктом вычислений в методе штрафных функций является вектор множителей Лагранжа:
-
для обратной штрафной функции;
-
для логарифмической штрафной функции.
Пример: Найти минимум в задаче
Решение: