3 Методы последовательной безусловной минимизации

3.1 Метод штрафов

Идея метода заключается в сведении задачи на условный минимум к решению последовательности задач поиска безусловного минимума вспомогательной функции:

,

где  - штрафная функция,  - параметр штрафа, задаваемый на каждой k-й итерации.

Штрафные функции конструируются, исходя из условий:

причём при невыполнении ограничений и  справедливо . Чем больше , тем больше штраф за невыполнение ограничений. Как правило, для ограничений типа равенств используется квадратичный штраф, а для ограничений типа неравенств – квадрат срезки:

,

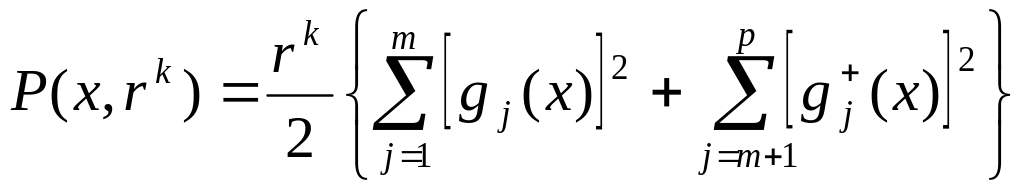где  - срезка функции:

Начальная точка поиска задаётся обычно вне множества допустимых решений X. На каждой k-й итерации ищется точка минимума вспомогательной функции  при заданном параметре  с помощью одного из методов безусловной минимизации. Полученная точка  используется в качестве начальной на следующей итерации, выполняемой при возрастающем значении параметра штрафа. При неограниченном возрастании  последовательность точек  стремится к точке минимума .

 

Алгоритм:

Шаг 1. Задать начальную точку ; начальное значение параметра штрафа ; число C > 1 для увеличения параметра; малое число  для остановки алгоритма. Положить .

Шаг 2. Составить вспомогательную функцию

.

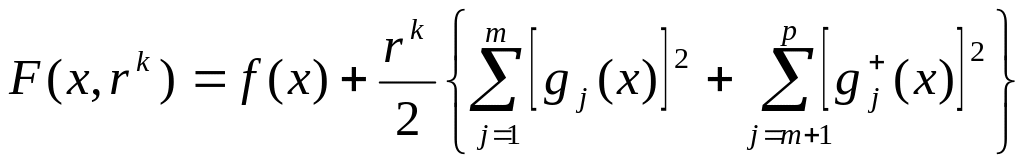Шаг 3. Найти точку  безусловного минимума функции  по x  с помощью какого-либо метода (нулевого, первого или второго порядка):

.

При этом задать все требуемые выбранным методом параметры. В качестве начальной точки взять . Вычислить .

Шаг 4. Проверить условие окончания:

а) если , процесс поиска закончить:

б) если , положить:  и перейти к шагу 2.

Утверждение 1 Пусть  - локально единственное решение задачи поиска условного минимума, а функции  и непрерывно дифференцируемы в окрестности точки . Тогда для достаточно больших  найдётся точка  локального минимума функции  в окрестности  и  при .

Замечания:

а) Так как сходимость метода обеспечивается при , то возникает вопрос о том, нельзя ли получить решение исходной задачи в результате однократного поиска безусловного минимума вспомогательной функции с параметром , равным большому числу, например . Однако такая замена последовательного решения вспомогательных задач не представляется возможной, так как с ростом  функция  приобретает ярко выраженную овражную структуру. Поэтому скорость сходимости любого метода безусловной минимизации к решению  резко падает. Так что процесс его определения заканчивается, как правило, значительно раньше, чем будет достигнута заданная точность, и, следовательно, полученный результат не даёт возможности судить об искомом решении .

б) Точки  в алгоритме – это точки локального минимума функции . Однако функция   может быть неограниченной снизу и процедуры методов безусловной минимизации могут расходиться. Это обстоятельство необходимо учитывать при программной реализации.

в) В методах штрафных функций имеется тесная связь между значениями параметров штрафа и множителями Лагранжа для регулярной точки минимума:

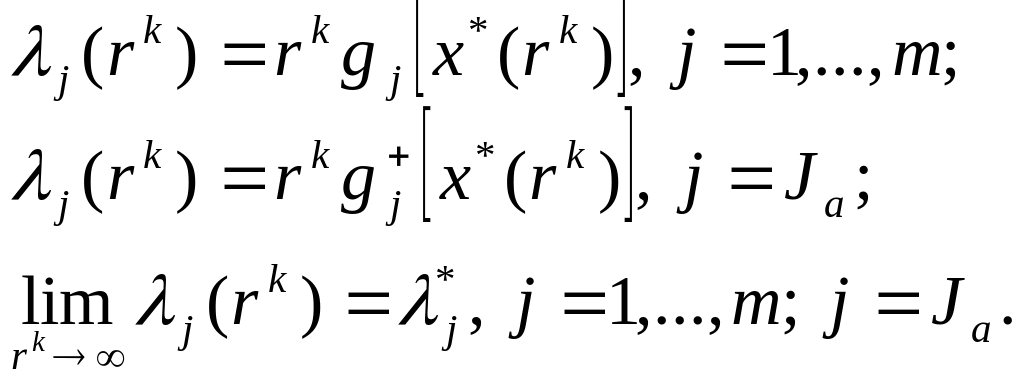
г) Обычно выбирается , а . Иногда начинают с , т.е. с задачи поиска безусловного минимума.

д) При решении задач процедура расчётов завершается при некотором конечном значении параметра штрафа . При этом приближённое значение, как правило, не лежит в множестве допустимых решений, т.е. ограничения задачи не выполняются. Это является одним из недостатков метода. С ростом параметра штрафа  генерируемые алгоритмом точки приближаются к решению исходной задачи извне множества допустимых решений. Поэтому обсуждаемый метод иногда называют методом внешних штрафов.

е) На практике для получения решения исходной задачи с требуемой точностью достаточно бывает решить конечное (относительно небольшое) число вспомогательных задач. При этом нет необходимости решать их точно, а информацию, полученную в результате решения очередной вспомогательной задачи, обычно удается эффектно использовать для решения следующей.

Пример: Найти минимум в задаче

Решение:

1. В поставленной задаче  (ограничения-равенства отсутствуют), . Решим задачу аналитически при произвольном параметре штрафа , а затем получим решение последовательности задач поиска безусловного минимума.

2. Составим вспомогательную функцию:

.

3. Найдем безусловный минимум функции  по x с помощью необходимых и достаточных условий:

Отсюда , но при этом не удовлетворяется условие , а также

.

В таблице приведены результаты расчётов при .

k
0	1		-3,66
1	2		-3,5	1
2	10		-3,166
3	100		-3,019
4	1000		-3,002
5		1	-3	2

Графическая иллюстрация дана на рисунке 3.1.

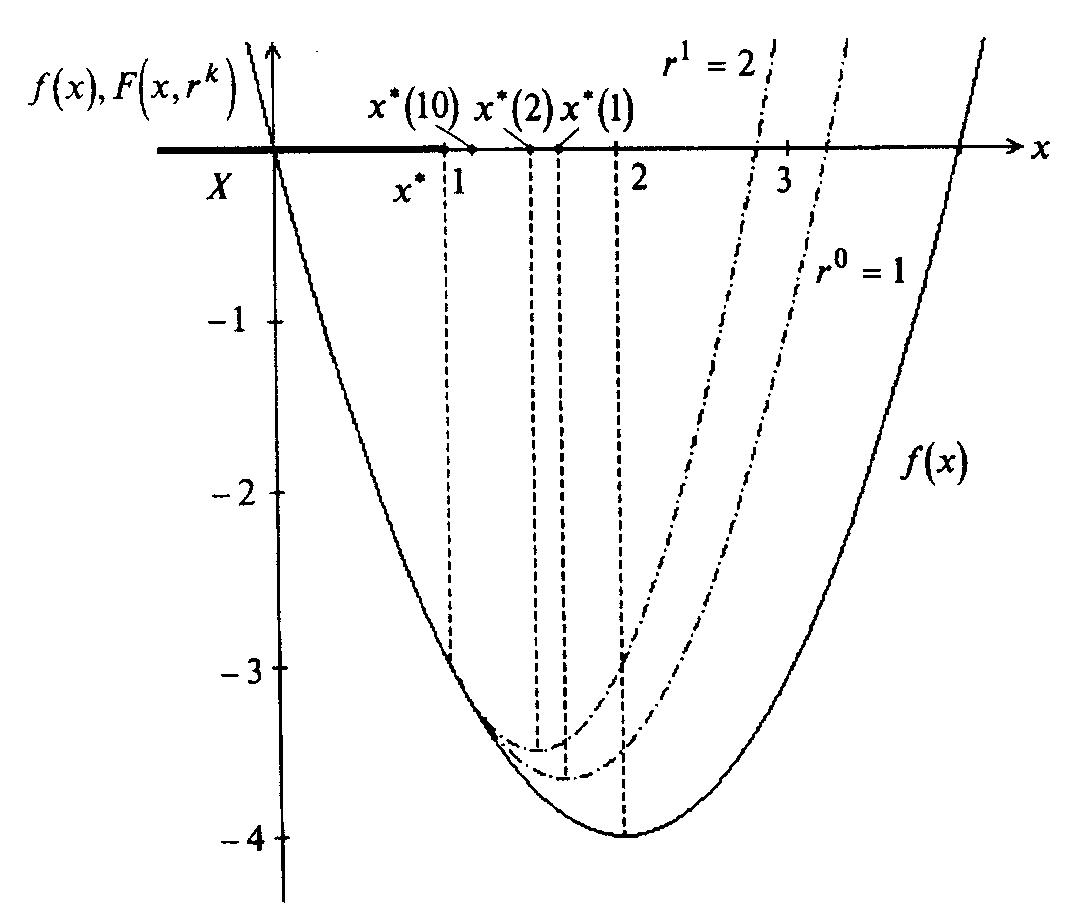
Рисунок 3.1

Так как  при , то достаточные условия минимума  удовлетворяются. При  имеем

Приведём решение этой задачи с помощью необходимых и достаточных условий экстремума.

Функция Лагранжа имеет вид

Необходимые условия минимума первого порядка:

а)      ;

б)      ;

в)      ;

г)       .

Решим систему для двух случаев.

В первом случае . Тогда из условия «а» получаем , что не удовлетворяет необходимым условиям минимума первого порядка.

Во втором случае . Поделим систему на  и заменим  на : . Из условия «г» имеем  или . При  из «а» следует, что , но при этом не удовлетворяется «б». При  имеем .

Достаточные условия минимума первого порядка удовлетворяются, так как  и число активных ограничений  (строка 1 в таблице). Согласно п. 3 замечаний получим

.