4.2 Метод Зойтендейка

Стратегия решения задачи методом Зойтендейка состоит в построении последовательности допустимых точек , таких, что . Правило построения точек последовательности :

,

где точка  - допустимая и такова, что

, (4.3)

 - множество индексов  активных ограничений, для которых выполнено условие (4.3); величина шага  находится в результате решения задачи одномерной минимизации:

                                                 (4.4)

Задача (4.4) может быть решена с использованием алгоритма применения необходимых и достаточных условий условного минимума. Иначе величину  следует выбирать из соотношения

,

где величина  определяется из условия , а величина ,  удовлетворяет условиям .

Направление спуска  удовлетворяет системе неравенств

(4.5)

Возможное направление спуска , удовлетворяющее условиям (4.5), определяется из решения задачи линейного программирования

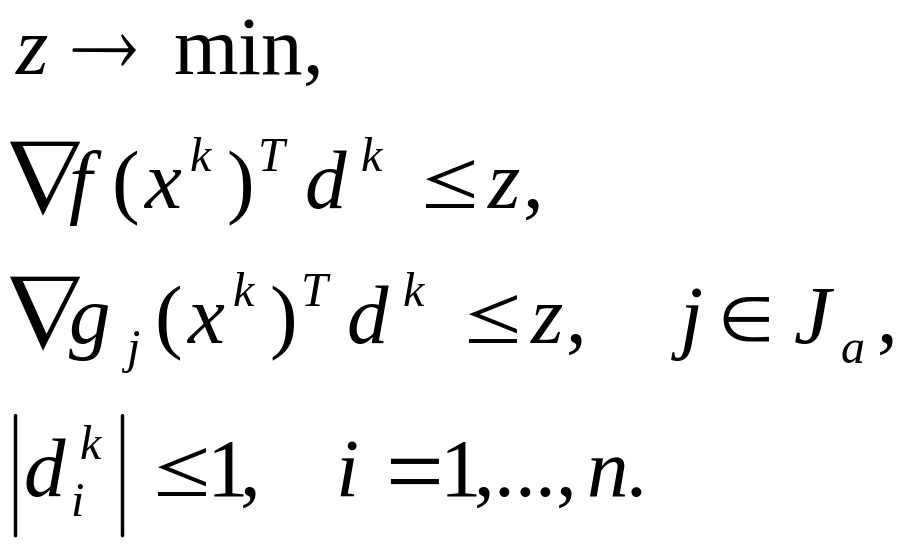  (4.6)

Если решение  задачи (4.6) меньше , то для поиска нового возможного направления спуска  полагают . Если же , то расчёт по усмотрению пользователя либо следует закончить, так как в точке  с точностью до  выполняются условия минимума в исходной задаче, либо продолжить, с целью добиться более высокой точности, положив , где .

Алгоритм:

Шаг 1. Задать , пердельное число итераций M, допустимую начальную точку , в которой .

Шаг 2. Положить k=0.

Шаг 3. Проверить условие :

а) если , расчет окончен;

б) если , перейти к шагу 4.

Шаг 4.Вычислить .

Шаг 5. Проверить выполнение условия . Сформировать множество индексов j, для которых условие выполнено. Если условие выполнено хотя бы для одного , то перейти к шагу 6. В противном случае положить и повторить вычисления на шаге 5.

Шаг 6. Записать систему неравенств

Шаг 7. Сформировать задачу линейного программирования

Шаг 8. решить задачу линейного программирования, сформированную на шаге 7. В результате находится искомое возможное направление спуска и - минимальное значение z.

Шаг 9. Вычислить шаг , решив задачу

Либо из соотношения , для чего следует:

а) найти величину из условия ;

б) определить величину , из условий (если условие выполняется только при , то не вычисляется). Если в точке ограничение с номером j активно и , то значение не вычисляется;

в) найти ;

г) вычислить значение .

Шаг 10. Найти точку .

Шаг 11. Вычислить величину .

Шаг 12. Проверить условие окончания:

а) если , то расчет может быть либо закончен, если точность удовлетворительна, либо продолжен при , . В первом случае - искомое приближенное решение исходной задачи, во втором – перейти к шагу 3;

б) если , то положить и перейти к шагу 3.

Замечания:

а) Если исходная задача не является задачей выпуклого программирования, в которой все функции , выпуклые, то алгоритм Зойтендейка сходится к точке , удовлетворяющей с точностью необходимым условиям минимума функции многих переменных при ограничениях типа неравенств. Следовательно, в точке должны быть проверены достаточные условия минимума.

б) Если исходная задача – задача выпуклого программирования и ее множество допустимых решений имеет внутренние точки, то найденная по алгоритму Зойтендейка точка есть решение исходной задачи.

в) Скорость сходимости алгоритма Зойтендейка оценивается как низкая по числу итераций.

Пример: Найти минимум в задаче

Решение:

1. Зададим , M =10.

2. Положим k = 0.

3⁰. Проверим условие : .

4⁰. Вычисляем .

5⁰. Проверяем выполнение условия :

.

Активным является ограничение .

6⁰. Записываем систему неравенств:

Имеем и .

7⁰. Записываем задачу линейного программирования

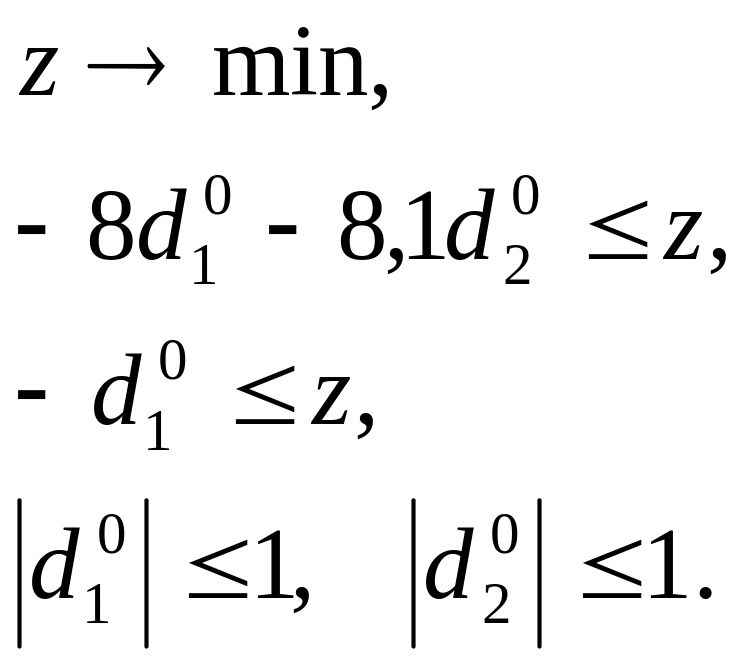
8⁰. Решаем задачу линейного программирования. Для этого приводим ее к каноническому виду, вводя следующие обозначения:

. Имеем:

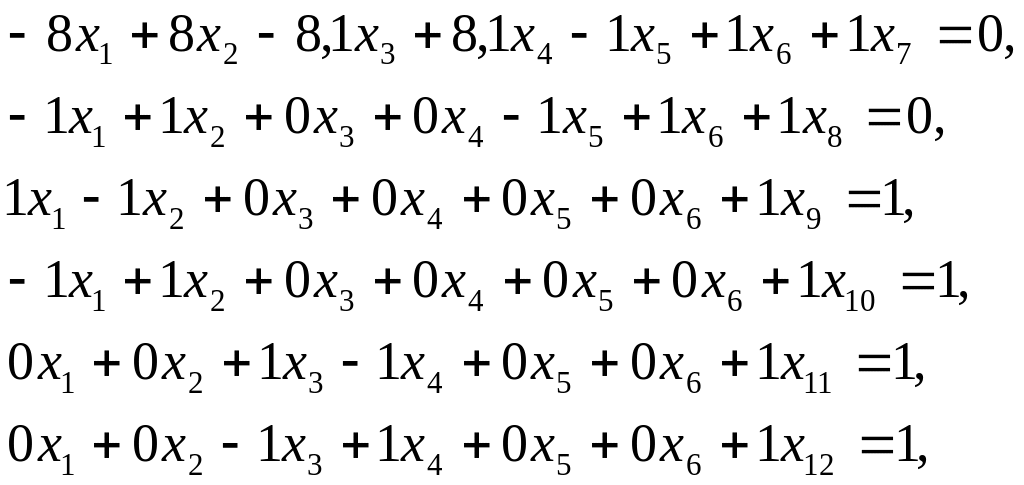
Решение задачи линейного программирования с использованием симплекс – метода имеет вид:

Поэтому .

9⁰. Вычисляем шаг . Имеем:

а)

б)

поскольку второе ограничение активно и , величина не вычисляется;

т.к. равенство выполняется только при , величина не вычисляется;

в) ;

г) .

10⁰. Получаем точку .

11⁰. Вычисляем .

12⁰. Проверяем условие окончания. Т.к. , то расчет окончен, точка есть найденное приближение точки .

Проанализируем полученную точку:

Т.к. решаемая задача есть задача выпуклого программирования, а множество имеет внутренние точки, то есть найденное приближенное решение задачи.