1.3. Геометрическая интерпретация и графический метод решения злп
В теории линейного программирования существуют две геометрические интерпретации решения ЗЛП. Первая интерпретация применяется для ЗЛП, записанной в стандартной форме, вторая – для ЗЛП, записанной в канонической форме.
Сначала рассмотрим с геометрической точки зрения представление множества допустимых планов стандартной ЗЛП на плоскости. Пусть количество ограничений m есть произвольное число, а количество переменных n равно 2. Тогда система ограничений ЗЛП в стандартной форме записи будет выглядеть следующим образом:
(1.17)
x1 , x2 0 (1.18)
Каждое из
неравенств системы ограничений (1.17) и
(1.18) представляет в пространстве
переменных x1 и
x2 полуплоскость
с границей, определяемой уравнением
прямой
,
x1 = 0, x2
= 0. Если система неравенств (1.17) с учетом
условия (1.18) совместна, тогда пересечение
всех этих полуплоскостей геометрически
представляет многоугольник возможных
решений системы, а именно – множество
допустимых планов рассматриваемой
задачи.
В линейном программировании множество допустимых планов с геометрической точки зрения может представлять собой:
выпуклый ограниченный многогранник;
выпуклый неограниченный многогранник;
пустое множество.
Графический метод решения злп
Рассмотрим ЗЛП с двумя переменными x1, x2 и m условиями-неравенствами:
(1.19)
(1.20)
При этом может быть наложено ограничение на переменные:
x1 , x2 0. (1.21)
Предположим, что множество допустимых планов ЗЛП (1.19) – (1.21) представлено в виде пятиугольника (рис. 1.5). Прямые, высекающие многоугольник OABCE на плоскости x1Ox2, определяются условиями (1.20) при m = 3 и (1.21), в которых знаки неравенства заменены на знаки равенства. Штриховка указывает общую часть пересечения полуплоскостей.
В этом многоугольнике необходимо найти такую точку, которая доставляла бы, например, максимум целевой функции (1.19). Поведение целевой функции может быть охарактеризовано с помощью линии уровня.
Определение 9. Линией уровня функции называется множество точек из области ее определения, в которых функция принимает одно и то же фиксированное значение.
Для
нашего случая линия уровня определяется
уравнением
.
Линия уровня, проходящая через начало
координат, имеет вид
.
x2
B
C
A
С(x)
D
О E x1
C(x) = const
Рис. 1.5. Графическая иллюстрация решения ЗЛП
Определение
10. Градиентом функции f
(x) = f
(x1, x2,…,
xn)
называется вектор
,
указывающий направление наиболее
быстрого возрастания функции.
Для линейной функции двух переменных линия уровня представляет собой прямую линию, перпендикулярную градиенту С(x):
.
Градиент показывает направление возрастания целевой функции.
Таким образом, с геометрической точки зрения решение ЗЛП сводится к определению такой точки множества допустимых планов D, через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Это означает, что для нахождения точки максимума необходимо построить линию уровня для некоторого произвольного значения целевой функции, например, нуля. Затем следует осуществлять ее параллельное перемещение так, чтобы она оставалась перпендикулярной вектору С(Х) до тех пор, пока не достигнет такой точки области D, из которой дальнейшее смещение в направлении вектора С(Х) было бы невозможно (выходим из области D).
Аналогично осуществляется поиск минимума целевой функции. Однако при этом движение по линиям уровня должно производится в направлении, обратном градиенту, т.е. по вектору –С(Х). Такой метод решения ЗЛП называется графическим.
На рис. 1.5 изображен некоторый частный случай, для которого решение ЗЛП (максимум целевой функции) достигается в точке C области D. Вообще возможны следующие варианты решения ЗЛП геометрическим методом.
На рис. 1.6 изображен случай, когда максимальное значение целевая функция принимает в любой точке отрезка BL. В этом случае линия уровня при перемещении в сторону увеличения значения целевой функции сливается с отрезком BL. Оптимальных планов будет бесконечное множество.
Аналогично, рис. 1.7 показывает, что оптимальными планами ЗЛП являются все точки луча AB. Рисунок 1.8 иллюстрирует ситуацию неограниченности целевой функции на множестве допустимых планов D, т.е. сколько бы мы ни перемещались по линиям уровня в направлении градиента, ее значение будет возрастать. Если же область допустимых планов состоит из одной единственной точки, то она является и оптимальным планом.
Отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
x2
x2
B
B
A
D
L
A
D
С(x)
K
С(x)
N
0
x1
0
M
x2
Рис. 1.6. Оптимальные планы Рис. 1.7. Оптимальные планы
отрезок BL луч AB
x2
B
D
M
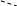A
С(x)
0 N x1
Рис. 1.8. Задача не разрешима, C(x) +
Итак, решение ЗЛП геометрическим методом состоит из следующих шагов.
На плоскости x1Ox2 строят прямые, уравнения которых получаются в результате замены в ограничениях (1.20) и (1.21) знаков неравенств на знаки равенств.
Находят полуплоскости, определяемые ограничениями.
Строят множество допустимых планов (многоугольник решений), если он существует.
Строят градиент С(x), указывающий направление возрастания целевой функции.
Строят линию уровня
,
проходящую через ноль.
Передвигают линию уровня параллельно самой себе либо в направлении вектора-градиента для ЗЛП на максимум, либо в противоположном направлении для задачи на минимум, в результате чего находят точку (точки), в которой целевая функция принимает максимальное (минимальное) значение, либо устанавливают неограниченность сверху (снизу) целевой функции на допустимом множестве.
В случае наличия оптимального плана вычисляют координаты точки (точек) максимума (минимума) функции и вычисляют значение целевой функции на оптимальном плане.
П р и м е р 1.5. Рассмотрим следующую задачу. Для производства изделий P1 и P2 предприятие использует три вида сырья S1, S2 и S3. Нормы расхода сырья каждого вида на одно изделие, общее количество сырья, которое может быть использовано предприятием, а также прибыль от реализации одного изделия приведены в табл. 1.1. Кроме того, маркетинговые исследования показали, что изделий вида P2 может быть реализовано не больше, чем изделий P1.