Приклади практичних завдань для самостійного опрацювання

1). За рис. 2.7 розрахувати ранні й пізні строки здійснення подій, а також їх резерви. Знайти критичний шлях виконання комплексу робіт і його довжину.

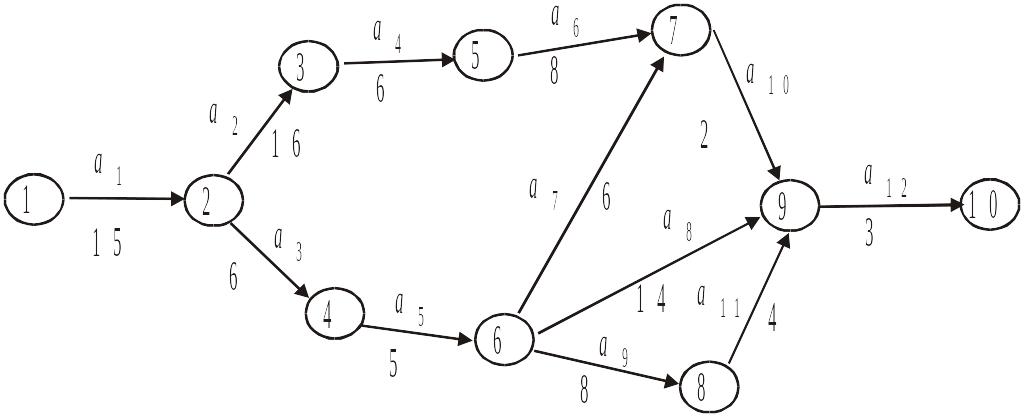
Рис. 2.7.

Розв'язок. Кожну вершину мережі розіб'ємо на чотири сектори. У верхній частині сектору відзначаємо номер події , у лівій – ранній строк здійснення події , у правій – пізній строк здійснення події й у нижній – резерв часу цієї події (рис. 2.8).

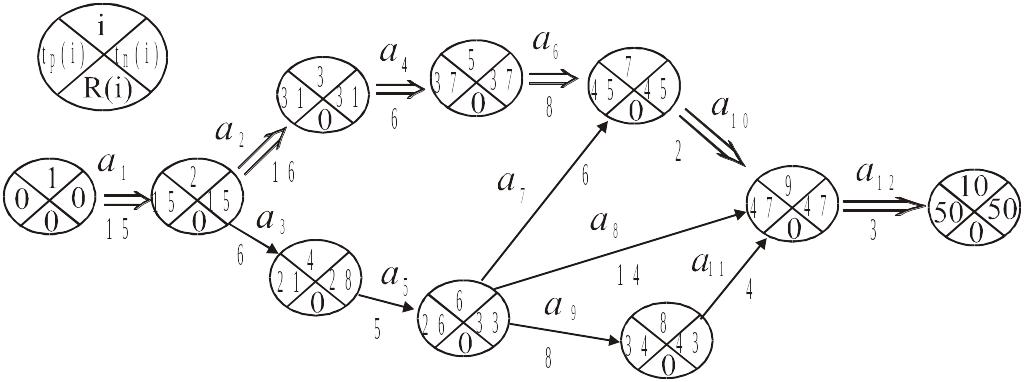
Рис. 2.8.

Спочатку за формулою (2.1) знаходимо ранні строки здійснення події й заносимо їх у ліві сектори мережевого графіка. Маємо:

;

;

;

;

;

;

;

;

;

.

Тепер розрахуємо пізні строки здійснення подій. Починаємо з останньої події й потім, «задкуючи», рухаємося до першої події.

Для = 10 пізній строк здійснення події . Далі по формулі (2.2) маємо:

;

;

;

;

;

;

;

;

.

Результати розрахунків заносимо в праві сектори вершин мережі.

По формулі (2.1) розрахуємо резерви часу кожної події й занесемо їх у нижні сектори вершин.

Наприклад:

;

;

;

і т.д.

Щоб визначити критичний шлях, фіксуємо події, що не мають резервів часу. Це події 1, 2, 3, 5, 7, 9, 10. Отже, шлях є критичним.

Довжина критичного шляху .

Критичний шлях відзначаємо на мережевому графіку подвійною стрілкою. Тепер перейдемо до параметрів робіт.

Окрема робота може початися в ранні, пізні або інші проміжні строки. Ранній строк початку роботи – це найбільш ранній (мінімальний) з можливих моментів початку даної роботи. Він, мабуть, збігається з раннім строком настання її початкової події, тобто

(2.7)

Тоді ранній строк закінчення роботи визначається по формулі

. (2.8)

Пізній строк закінчень роботи – найбільш пізній момент часу закінчення цієї роботи, після якого залишається стільки часу, скільки його необхідно для виконання всіх наступних робіт. І тому що жодна робота не може скінчитися пізніше припустимого пізнього строку своєї кінцевої події , пізній строк закінчення робіт визначається співвідношенням , (2.9)

а пізній строк початку цієї роботи – співвідношенням

. (2.10)

З формул (2.7)-(2.10) видно, що моменти початку й закінчення роботи тісно пов'язані із сусідніми подіями.

2). Обчислити для мережевого графіка, зображеного на рис. 2.7, ранні й пізні строки початку й закінчення робіт, їх повні й вільні резерви часу. Знайти всі повні шляхи, обчислити їхню довжину й резерви часу. Побудувати мережевий графік у масштабі часу.

Розв'язок. Щоб знайти зазначені параметри робіт, використовуємо формули (2.6)-(2.9), а також результати розв'язку попереднього прикладу, оформлені у вигляді мережевого графіка (рис. 2.8). Результати розрахунків зведемо в табл. 2.3.

Графа 3 заповнюється за допомогою мережевого графіка (рис. 2.8). Послідовно виписуються числа, що стоять у лівих секторах кружків. Графу 4 заповнюють, складаючи числа граф 2 і 3. Потім заповнюємо графу 6, вибираючи послідовно числа із правих секторів кружків мережевого графіка.

Таблиця 2.3.

Робота		Строки виконання				Резерви часу робіт
		ранні		пізні
1	2	3	4	5	6	7	8
	15 16 6 6 5 8 6 14 8 2 4 3	0 15 15 31 21 37 26 26 26 45 34 47	15 31 21 37 26 45 32 40 34 47 38 50	0 15 22 31 28 37 39 33 35 45 43 47	15 31 28 37 33 45 45 47 43 47 47 50	0 0 7 0 7 0 13 7 9 0 9 0	0 0 0 0 0 0 13 7 0 0 9 0

Графа 5 дорівнює різниці граф 6 і 2. Графа 7 дорівнює різниці граф 6 і 4. Графа 8 заповнюється на основі формули . Тут числа беруться з лівих кружків графіка, а – із графи 4. Для роботи . Вона кінчається в секторі кружка, що моделює подію 2, тому . Із графи 4 маємо . Значить . Для роботи маємо ; . Тому і т.д. Виявимо тепер усілякі повні шляхи для виконання робіт комплексу, знайдемо їхню довжину, а також резерви часу.

– критичний шлях;

;

;

.

Довжина цих шляхів:

днів;

днів;

дня;

день.

Таким чином, тривалість максимального шляху рівна 50 дням, за цей час усі роботи комплексу будуть виконані, тобто 50 днів – це мінімальний час для виконання всіх робіт комплексу.

Визначимо резерви часу по виявлених шляхах. Використовуючи формулу (2.6), одержимо:

днів;

днів;

днів;

днів.

У межах наявних резервів часу загальний строк виконання робіт не збільшується, якщо не збільшилася тривалість виконання кожної з робіт критичного шляху.

Для наочності виявлення резервів часу побудуємо мережевий графік робіт (рис. 2.9) у масштабі часу.

Побудова починається із критичного шляху відповідно до правил мережного моделювання з урахуванням зображення тривалості робіт у масштабі часу по осі абсцис. По осі ординат довжина стрілок вибирається з міркувань зручності сприйняття мережі в цілому. Цим пояснюється, наприклад, більша довжина стрілки роботи у порівнянні з , хоча за масштабом часу . У результаті одержимо мережевий графік, зображений на рис. 2.9.

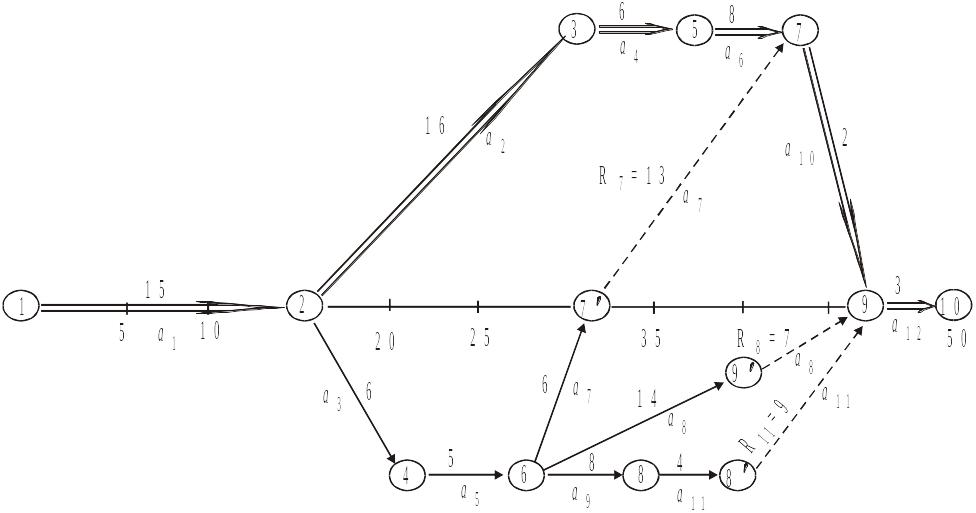
Рис. 2.9. Мережевий графік робіт у масштабі часу

При побудові мережевого графіка в масштабі часу ми зустрічаємося з необхідністю введення фіктивних робіт , , (пунктирні стрілки) і фіктивних подій , , . Час виконання цих фіктивних робіт дорівнює нулю, а їх структура показує розташування вільних резервів часу:

днів;

днів;

днів.

2). Знайти коефіцієнт напруженості роботи , зображеної на рис. 2.8.

Розв'язок. Максимальний шлях, що проходить через роботу , – це шлях

;

дня.

Незбіжні відрізки цього шляху й критичного шляху укладено між подіями 2 і 9. Для шляху – це відрізок ; а для критичного шляху – відрізок .

Відрізок шляху , що збігається із критичним шляхом, – це й , довжина якого рівна ; довжина критичного шляху . Підставимо знайдені величини у формулу (2.11):

. (2.11)

Формулу (2.11) можна привести до виду:

. (2.12)

Коефіцієнт напруженості може змінюватися в межах від 0 (для робіт, у яких відрізки максимального зі шляхів, що не збігаються із критичним шляхом, складаються з фіктивних робіт нульової тривалості) до 1 (для робіт критичного шляху).

Чим ближче до 1 коефіцієнт напруженості, тем складніше виконати дану роботу у встановлений термін, а чим ближче він до нуля, тем більший відносний резерв має максимальний шлях, що проходить через дану роботу.

Роботи можуть мати однакові повні резерви, але різний ступень напруженості. І навпаки, різним повним резервам можуть відповідати однакові коефіцієнти напруженості.

З формули (2.12) видно, що величина коефіцієнта напруженості залежить від і . Чим повний резерв часу більше виконання деякої роботи й , (тобто чим менше – відрізок часу максимального шляху, що проходить через цю роботу й не співпадаючого із критичним шляхом), тим більше буде дріб, що стоїть в правій частині формули (2.12), і чим менше коефіцієнт напруженості цієї роботи, тем легше буде її виконати. У загальному випадку зазначений дріб визначає питому вагу повних резервів часу робіт у тривалості відрізків максимальних шляхів, що не збігаються із критичним шляхом. Чим більше ця питома вага, тем менше коефіцієнт напруженості.

3). Провести оптимізацію мережевого графіка (рис. 2.9) за критерієм мінімуму часу виконання всіх робіт комплексу; побудувати оптимальний мережний план робіт; визначити економію. За умови, що ; ; ; ; ; ; ; ; ; ; ; .

Розв'язок. Виявлені вільні резерви дозволяють провести оптимізацію мережевого графіка, пов'язану із кращим перерозподілом виділених ресурсів, і побудувати план виконання всього комплексу робіт за менший час, тобто більш ощадливий.

Оптимізацію мережевого графіка будемо проводити шляхом перенесення частини коштів з некритичних робіт на критичні, фіксуючи при цьому номера робіт, з яких кошти знімаються й на які переносяться.

Переносячи резерви з некритичних робіт на критичні, ми будемо збільшувати некритичний шлях і зменшувати критичний доти, поки не збіжаться тривалості всіх шляхів.

Розташуємо тривалості всіх шляхів послідовно в порядку збільшення їх резервів і почнемо оптимізацію з першої пари шляхів і .

На першому етапі оптимізації переносимо резерви з некритичного шляху некритичної роботи , що має вільний резерв часу днів. Беремо частину коштів роботи й переносимо на роботу критичного шляху. Ці кошти на роботі позначимо . Тоді тривалість нових критичних шляхів: . Величину коштів можна визначити, розв'язавши систему:

(2.13)

при обмеженні

За умовою: ; ; ; ; ; ; . Тому система (2.13) прийме вид:

Звідси: .

Обмеження виконане.

Нові часи виконання робіт і знаходять по формулах: ; ; новий критичний строк .

Маємо:

;

;

.

На другому етапі розглядаємо наступний найближчий некритичний шлях , на якому у роботи є вільний резерв часу:

.

Частина коштів , що знімається з роботи , повинна задовольняти умові .

Кошти перенесемо на роботу в кількості й на роботу в розмірі для прискорення виконання робіт першого й третього шляхів.

Для знаходження величин цих коштів складемо систему рівнянь:

(2.14)

Підставимо в систему (2.14): ; ; ; ; ; ; ; .

Маємо:

Отже, ; ; .

Обмеження виконане.

Новий час виконання робіт , , знаходимо по формулах:

; ; .

Маємо:

;

;

.

Новий критичний шлях:

.

На третьому етапі розглядаємо на останньому путі наявність резерву часу в роботі . Вільний резерв часу в роботі рівний:

.

Знімаємо кошти й записуємо умову допустимості . Переносимо резерви некритичної роботи на роботи , , інших критичних шляхів у розмірах , , відповідно й складаємо систему рівнянь

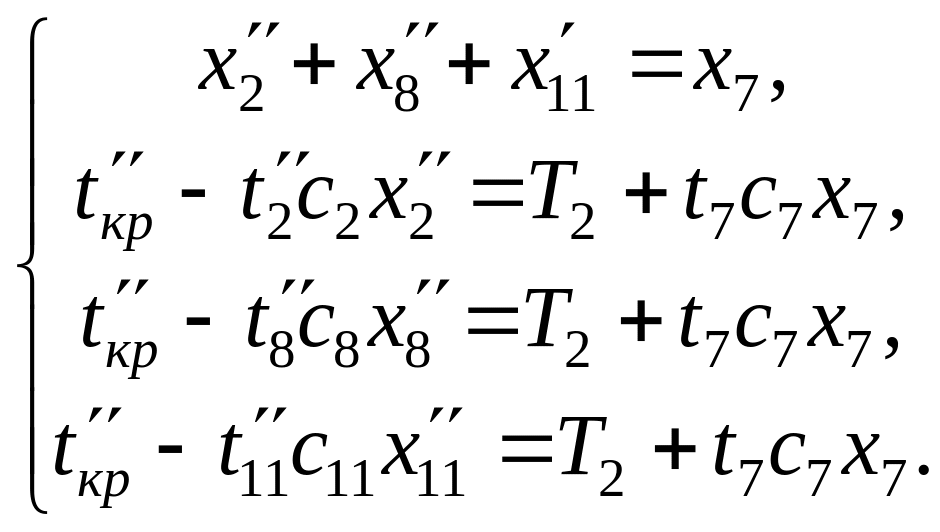(2.15)

Розв'язуючи цю систему при числових даних: ; ; ; ; ; ; ; ; ; ,

одержимо: ; ; ; .

Обмеження виконане.

Новий час виконання робіт , , , обчислюється по формулах:

;

;

;

.

Новий критичний шлях:

доби.

Економія 50 – 43,3 = 6,7 доби.

Побудуємо оптимальний план робіт (рис. 2.10).

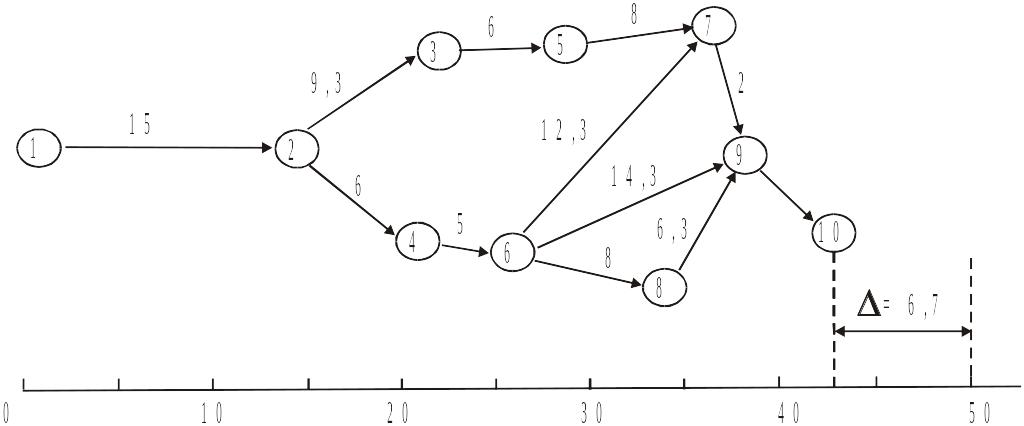
Рис. 2.10.