12.3. Понятие о множественной корреляции
Корреляционный
анализ системы случайных величин (Х1,
Х2,
…, Хm)
предусматривает прежде всего исследование
взаимного влияния каждой пары составляющих.
В результате получают оценки парных
коэффициентов корреляции
,
совокупность которых составляет
корреляционную
матрицу
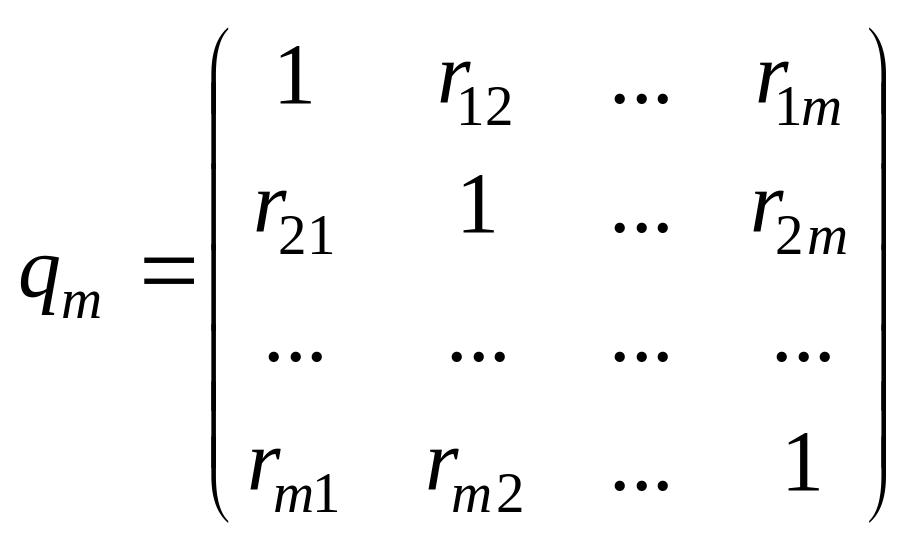
Известно, что на результативный признак воздействуют не только отдельно взятые факториальные признаки Хi, но и их взаимное влияние. Чтобы выявить связь между двумя из них, исключив влияние остальных признаков, вводят понятие частного коэффициента корреляции.
Коэффициент линейной
корреляции между составляющими Xk
и
Xj
системы
,
вычисленный при условии, что l
из оставшихся
m–2
факто-риальных признаков зафиксированы,
называется частным
коэффициентом корреляции l-го
порядка. Его выборочная оценка обозначается
где
(
)
- номера фиксированных признаков.
Для вычисления частного коэффициента корреляции l-го порядка составляют вспомогательную матрицу порядка l+2 из элементов матрицы qm , индексы которых соответствуют индексам коэффициентов частной корреляции (при l = m 2 используется вся матрица qm ).
В частности,
выборочный коэффициент корреляции
является мерой линейной связи между
составляющими X1
и X2
при
фиксированных Х3,
…, Хm
и вычисляется по формуле
(12.8)
где
алгебраические дополнения элементов
корреляционной матрицы qm.
Общую корреляционную
связь одного из признаков Xk
системы
со всеми остальными ее составляющими
можно определить с помощью множественного
(совокупного) коэффициента корреляции,
оценкой которого является величина
,
(12.9)
где
- определитель корреляционной матрицы
- алгебраическое
дополнение элемента
этой матрицы.
12.15. Даны
результаты 15 наблюдений над системой
случайных величин
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Х1 |
9,8 |
8,2 |
7,6 |
8,5 |
5,9 |
9,3 |
12,9 |
12,3 |
11,7 |
9,9 |
13,0 |
14,0 |
14,9 |
7,5 |
8,1 |
Х2 |
57,5 |
44,1 |
40,2 |
44,4 |
30,8 |
47,3 |
78,5 |
62,7 |
60,5 |
55,7 |
72,8 |
73,9 |
80,7 |
38,9 |
42,7 |
Х3 |
50,2 |
28,3 |
15,0 |
21,8 |
2,0 |
35,4 |
98,0 |
67,3 |
59,7 |
52,0 |
83,5 |
87,1 |
101 |
14,9 |
23,0 |
Х4 |
12,0 |
7,1 |
4,3 |
5,1 |
1,4 |
7,4 |
15,9 |
11,8 |
12,2 |
9,8 |
15,7 |
14,9 |
18,5 |
4,7 |
5,5 |
Требуется: а)
составить выборочную корреляционную
матрицу; б) вычислить выборочный частный
коэффициент корреляции
между признаками Х1
и
Х2 при
фиксированном Х3;
в) определить множественный коэффициент
корреляции R1.
Сначала вычислим выборочные средние, несмещенные средние квдратичные отклонения данных признаков и их парные корреляционные моменты:
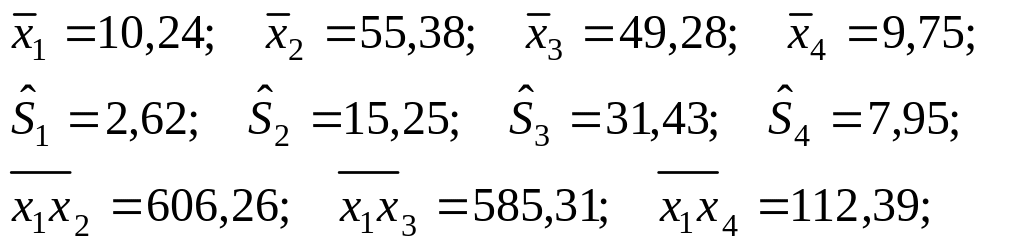
Теперь вычислим парные коэффициенты корреляции и составим корреляционную матрицу.
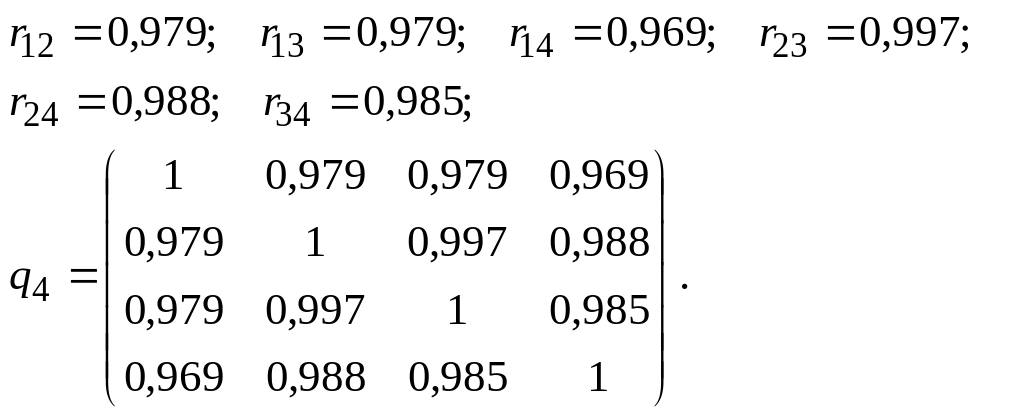
Чтобы вычислить
выборочный частный коэффициент корреляции
,
составим вспомогательную матрицу,
состоящую из элементов корреляционной
матрицы, индексы которых имеют цифры
1, 2 и 3:
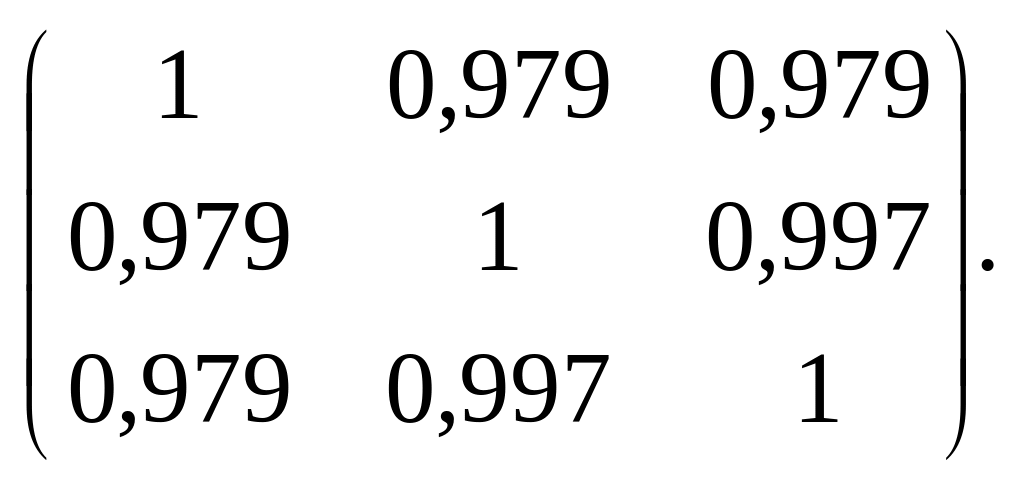
Вычисляем
алгебраические дополнения элементов
этой матрицы.
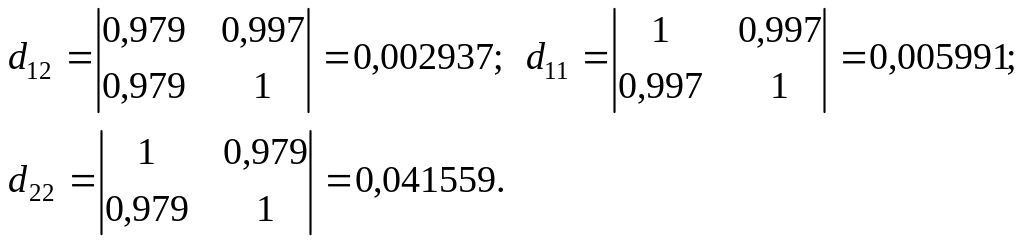
Наконец, вычисляем частный коэффициент корреляции :
Множественный коэффициент корреляции R1 характеризует влияние факториальных признаков Х2, Х3, Х4 на результативный признак Х1 :
где
Отсюда
Как видно, обобщенный коэффициент корреляции весьма близок к единице, что говорит об очень сильной корреляционной связи между данными признаками.
12.16. Дана
выборка значений системы трех случайных
величин. Требуется: а) составить
корреляционную матрицу q3;
б) вычислить частные коэффициенты
корреляции
в) вычислить множественные коэффициенты
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Х1 |
11,5 |
19,5 |
28,2 |
35,3 |
25,3 |
22,1 |
15,6 |
10,5 |
38,1 |
4,6 |
Х2 |
12,6 |
10,0 |
10,4 |
12,7 |
11,6 |
12,4 |
8,2 |
9,4 |
12,4 |
7,4 |
Х3 |
12,3 |
11,2 |
5,66 |
3,59 |
5,43 |
5,98 |
10,5 |
14,6 |
1,75 |
16,8 |
№ |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Х1 |
13,6 |
18,5 |
18,2 |
25,3 |
26,3 |
29,3 |
20,6 |
16,5 |
35,1 |
9,6 |
Х2 |
11,6 |
10,8 |
10,4 |
11,7 |
16,4 |
14,4 |
9,2 |
11,4 |
13,4 |
9,4 |
Х3 |
13,5 |
12,4 |
7,24 |
5,36 |
3,52 |
8,48 |
13,5 |
11,6 |
2,45 |
15,1 |