Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

«ВОДОРОДОПОДОБНЫЙ АТОМ»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к решению задач по атомной физике

для студентов физического факультета

Ростов-на-Дону

2006

Методические указания разработаны кандидатом физико-математических наук, ассистентом кафедры нанотехнологии И.Н. Леонтьевым и кандидатом физико-математических наук, зав. кафедрой нанотехнологии Ю.И. Юзюком.

Ответственный редактор канд. физ.-мат. наук И.Н. Леонтьев

Компьютерный набор и верстка инженер Г.А. Колесников

Печатается в соответствии с решением кафедры общей физики физического факультета РГУ, протокол № 21 от 25 апреля 2006 г.

Основные формулы

1.Первый постулат Бора (условие стационарности орбит):

Из бесконечного множества электронных орбит, возможных с точки зрения классической механики, осуществляются в действительности только некоторые дискретные орбиты (стационарные состояния), для которых момент импульса электрона удовлетворяет следующему условию:

,

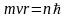где m–масса электрона, v – скорость электрона на орбите радиуса r, n – номер орбиты (главное квантовое число n=1,2,3..), 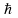– постоянная Планка.

Электрон, находящийся на одной из этих орбит, несмотря на то, что он движется с ускорением, не излучает электромагнитных волн.

2. Второй постулат Бора

При переходе атома из стационарного состояния с большей энергией E_i в стационарное состояние с меньшей энергией E_j происходит излучение кванта света (фотона) с энергией :

,

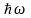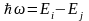где  – циклическая частота излучения при переходе с i-ой на j-ю орбиту (i>j), E_i и E_j - энергии электрона на этих орбитах.

Такое же соотношение выполняется и в случае поглощения фотона, когда атом переходитс низшего энергетического уровня E_j на более высокий уровень E_i.

3. Обобщенная формула Бальмера:

Излучение невзаимодействующих друг с другом атомов состоит из отдельных спектральных линий, причем они расположены не беспорядочно, а объединяются в группы или, как их называют, серии линий. Было обнаружено, что частоты волн в различных сериях, описываются следующей формулой – формулой Бальмера:

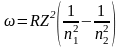где ,

где  – циклическая частота перехода между состояниями с квантовыми числами n₁ и n₂, R – постоянная Ридберга, Z – заряд ядра (в единицах е), k = 1/4_o, _o – диэлектрическая постоянная, ( n₁=1 – серия Лаймана, n₁ =2 – серия Бальмера, n₁=3 – серия Пашена, n₁=4 – серия Брэкета, n₁=5 – серия Пфунда, n₁=6 – серия Хэмфри).

Серия Лаймана находится в ультрафиолетовой части спектра, видимой части спектра принадлежит серия Бальмера, остальные серии лежат в инфракрасной области.

Задача №1

В классической электродинамике показывается, что электрон, движущийся с ускорением a, излучает в единицу времени энергию , где k=1/4₀. Оценить на основе классических представлений «время жизни» атома, считая, что полное ускорение совпадает с центростремительным.

Для простоты будем считать, что электрон в любой момент времени, до падения на ядро, движется равномерно, по круговой орбите. Причем будем считать, что в момент времени t=0 электрон движется по первой боровской орбите, т.е. r₁=0.5310^-10м. Тогда согласно 2-му Закону Ньютона

.

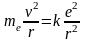
Тогда кинетическая энергия электрона K и ускорение а будут равны

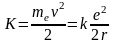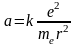, (1)

и полная энергия электрона в поле ядра

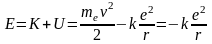. (2)

Очевидно, что энергия, которая будет излучаться за время dt ,будет равна убыли полной энергии электрона dE, тогда

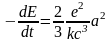или .

Подставляя в формулу (3), выражения для полной энергии Е (2) и ускорения а (1), получим

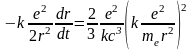. (3)

Разделяя переменные, получим

.

Проинтегрируем это уравнение: левую часть по r от r₁ до 0, а правую по t от 0 до .

.

В результате получим

.

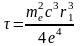Подставляя в последнее выражение численные значения, получим  = 1.310^-11с.

Задача №2

Частица массы m движется по круговой орбите в центрально симметричном потенциальном поле U=r²/2 . Найти, используя условия квантования Бора, разрешенные радиусы орбит и уровни энергии частицы.

Если потенциальное поле обладает сферической симметрией, то

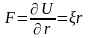. (4)

Исходя из второго закона Ньютона

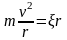. (5)

Согласно правилу квантования Бора

, где n = 1,2,3… .. (6)

Выражая из (6) скорость частицы v и подставляя в (5) найдем возможные значения r:

.

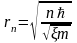Возможные значения полной энергии будут описываться следующим уравнением:

.

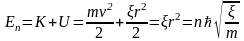Задача №3

Определить для водородоподобного иона радиус n-ой боровской орбиты и скорость электрона на ней. Вычислить эти величины для первой боровской орбиты атома водорода и ионов Не⁺ и Li⁺⁺.

Поскольку электрон двигается по круговой орбите, то

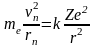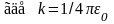, , (7)

где r_n – радиус n – ой орбиты, v_n – скорость электрона на n – ой орбите.

Согласно правилу квантования Бора

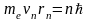. (8)

Откуда . Подставляя выражение, полученное для v_n в (7), получим

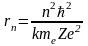. (9)

Подставив (9) в (8), получим выражение для v_n

.

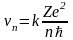Значения радиуса первой боровской орбиты r₁ и скорости электрона на ней v₁, для атомов водорода и ионов Не⁺ и Li⁺⁺, приведены в таблице 1.

Таблица 1.

	v1, 106 м/с	r1, 10-10м
Н	2.19	0.529
He+	4.37	0.265
Li++	6.56	0.176

Задача №4

Интерпретировать квантовые условия Бора на основе волновых представлений: показать, что стационарным боровским орбитам соответствует целое число дебройлевских волн. Найти длину волны электрона на n-ой орбите.

На стационарной боровской орбите будет укладываться целое число дебройлевских волн, если

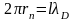где l = 1,2,3. (10)

По определению длина волны де Бройля равна (в случае если электрон движется на n - ой боровской орбите)

,

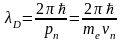где p_n – импульс электрона на n - ой боровской орбите, - скорость электрона на n - ой боровской орбите (см. задачу №2 ). Отсюда

(11)

Подставим полученное выражение для _D в (10) и, учтя, что радиус на n - ой боровской орбиты равен

,

получим

.

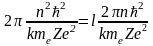Откуда l = n. Т.к. n целое положительное число, то мы можем сделать вывод, что на любой стационарной боровской орбите любого водородоподобного иона укладывается целое число дебройлевских длин волн.

Задача №5

Какова величина тока, соответствующего движению электрона на n-ой орбите атома водорода (n=1)?

По определению сила эквивалентного кругового тока равна:

.

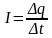При движении электрона по орбите за время равное одному периоду Т переносится заряд е (е – заряд электрона). Отсюда

.

Период обращения электрона на n - ой орбите равен

,

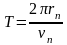где 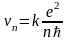– скорость электрона на n – ой орбите (см. задачу№2);

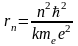– радиус n - ой орбиты.

Отсюда

.

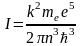Подставляя числовые значения и произведя вычисления для первой боровской орбиты (n = 1) получаем I = 1,0610^-3 А.

Задача №6

Электрон в атоме водорода движется вокруг ядра по круговой орбите некоторого радиуса. Найти отношение магнитного момента p_m эквивалентного кругового тока и к моменту импульса L орбитального движения электрона.

Магнитный момент p_m эквивалентного кругового тока и момент импульса L электрона, двигающегося по n - ой орбите, по определению равны

,

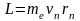где 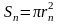– площадь контура, ограниченного n - ой орбитой,

– сила эквивалентного кругового тока, v_n – скорость электрона на n - ой орбите, r_n – радиус n - ой орбиты. Отсюда

.

Задача №7

Найти для водородоподобных ионов кинетическую энергию К электрона и его энергию связи Е_св в основном состоянии, а также потенциал ионизации _i. Вычислить эти величины для атома водорода и ионов Не⁺ и Li⁺⁺.

В предыдущей задаче было найдено значение скорости электрона на n - ой орбите. Оно имеет вид:

,

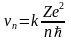Выражение для кинетической энергии электрона, находящегося на n - ой боровской орбите будет иметь следующий вид:

.

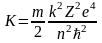А поскольку k²me4/2ћ³ = R - постоянная Ридберга, выражение для кинетической энергии электрона на n - ой боровской орбите примет вид

Полная энергия электрона (находящегося на n - ом уровне) в кулоновском поле ядра равна

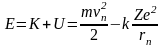
Используя выражения для v_n и r_n, полученные в задаче №3, получаем

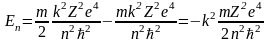
Состояние атома с наименьшей энергией (n = 1) называют основным. Эта энергия (по модулю) является энергией связи электрона в основном состоянии Е_св = Е₁. Именно эту энергию надо сообщить электрону в основном состоянии (n = 1), чтобы удалить его из атома. Таким образом, потенциал ионизации _i будет определяться следующим выражением:

.

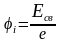Значения кинетической энергии K, энергии связи Е_св и потенциал ионизации 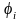для атома водорода и ионов He⁺ и Li⁺⁺ приведены в таблице 2.

Таблица 2

	K, эВ	Есв, эВ	i, В
Н	13.6	13.6	13.6
He+	54.5	54.5	54.5
Li++	122.5	122.5	122.5

Задача №8

Определить первый потенциал возбуждения φ₁ и длину волны резонансной линии (головной линии серии Лаймана) для атома водорода и ионов He⁺ и Li⁺⁺.

Первый потенциал возбуждения φ₁ соответствует переходу электрона из основного состояния n₁ = 1 на уровень с n₂ = 2.

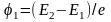
Поскольку

,

то

.

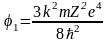Учитывая, что

,

выражение для первого потенциала возбуждения приобретает следующий вид

.

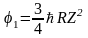Для нахождения длины волны в головной линии серии Лаймана воспользуемся обобщенной формулой Бальмера

.

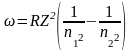Поскольку в нашем случае n₁ = 1, n₂ = 2, то

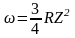
и, используя связь частоты с длиной волны, окончательно получим

.

Значения первого потенциала возбуждения φ₁ и длины волны λ головной линии серии Лаймана для атома водорода и ионов He⁺ и Li⁺⁺ представлены в таблице 3.

Таблица 3

	, нм	1, В
Н	121.5	10.2
He+	30.4	40.8
Li++	13.5	91.5

Задача №8

Вычислить длину волны  спектральной линии атомарного водорода, частота которой равна разности частот следующих двух линий серии Лаймана: ₁=102.6 нм, ₂=97.27 нм. Какой серии принадлежит эта линия?

Для вычисления длины волны некоторой спектральной линии атомарного водорода (Z = 1) воспользуемся формулой Бальмера:

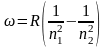(12)

или с учетом связи частоты и длины волны получим:

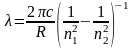. (13)

Для линий серии Лаймана (n = 1) это уравнение будет иметь вид:

, ,

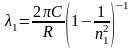отсюда

, ,

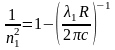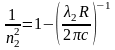подставляя в (13) получим

.

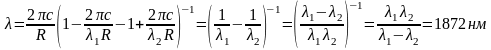Рассчитав значение n₁ определим к какой серии принадлежит эта линия

,

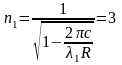т.е линия принадлежит серии Пашена.

Задача №9

У какого водородоподобного иона разность длин волн головных серий Бальмера и Лаймана равна 59,3 нм?

Для определения типа водородоподобного иона воспользуемся обобщенной формулой Бальмера

. (14)

Поскольку для головной линии серии Бальмера n₁ = 2, n₂ = 3, а для головной линии серии Лаймана n₁ = 1, n₂ = 2. То (14) для головной линии серии Бальмера примет вид:

,

а для головной линии серии Лаймана

.

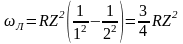Учтя связь частоты с длиной волны, получим

.

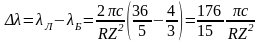Откуда

.

Что соответствует иону Li⁺⁺.

Задача №10

В спектре некоторых водородоподобных ионов длина волны третьей линии серии Бальмера равно 108,5 нм. Найти энергию связи электрона в основном состоянии этих ионов.

Запишем обобщенную формулу Бальмера

. (15)

Для третьей линии серии Бальмера n₁ = 2, n₂ = 5, тогда, с учетом того что

,

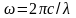выражение (15) примет следующий вид:

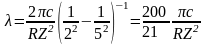. (16)

Поскольку (см. задачу №7)

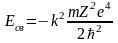и ,

то

.

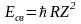Тогда с учетом (16) получим

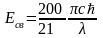=54.5 эВ.

Это энергия связи электрона в основном состоянии иона He⁺.

Задача №11

Учитывая движение ядра атома водорода и боровское условие квантования, найти: 1) возможные расстояния между электроном и ядром; 2) возможные значения полной кинетической энергии; 3) энергию связи электрона; 4) на сколько процентов отличается энергия связи и постоянная Ридберга, полученные без учета движения ядра, от соответствующих уточненных значений этих величин.

Пусть R и r – расстояния, соответственно от ядра и электрона до общего центра вращения. Тогда согласно 2-му Закону Ньютона

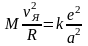
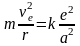, (17)

, М и m – массы ядра и электрона, соответственно, v_Я и v_е – их скорости, а – расстояние между ядром и электроном, равное R + r.

Согласно правилу квантования Бора

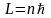, где n = 1,2,3…,

где L – момент импульса, равный в данном случае,

,

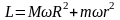тогда

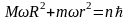. (18)

Используя связь линейной и угловой скорости

,

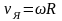
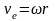перепишем (17) в следующем виде

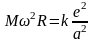
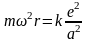(19)

или

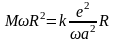
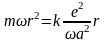
Подставляя, полученные выражения в (18), получим

.

Отсюда

.

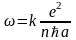Подставив найденное выражение для  в (19) найдем выражения для R и r

, .

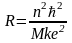Отсюда

,

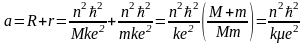где 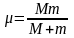– приведенная масса.

Полная кинетическая энергия атома водорода в данном случае будет складываться из кинетической энергии вращательного движения ядра К_Я и электрона К_е

.

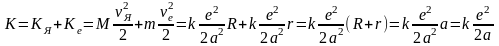Подставляя сюда выражение, найденное выше для а, получим

.

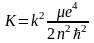Полная энергия системы равна сумме кинетической и потенциальной энергий

.

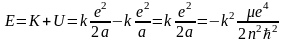Тогда выражение для энергии связи (n = 1) будет иметь следующий вид:

,

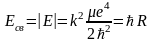где – уточненное выражение для постоянной Ридберга.

Сравнивая полученные выражения для постоянной Ридберга R и энергии связи Е_св с аналогичными выражениями, полученными нами ранее, но без учета движения ядра (т.е M = ), можно видеть, что

.

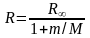
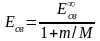Подставляя численные значения, оказывается, что разница составляет 0,055%. Несмотря на столь малое различие, его удается зафиксировать с помощью современных спектральных приборов.