2.7. Однородный фильтр

Однородным называется нерекурсивный фильтр, у которого все коэффициенты системной функции одинаковы. Этот фильтр называют также фильтром скользящего среднего. Схема фильтра приведена на рисунке 2.21.

Рисунок 2.21 – Однородный фильтр

Из рисунка видно, что выходной сигнал фильтра определяется следующими соотношениями

Определим Z-преобразования последовательностей v_n и y_n

Определим системную функцию фильтра

.

Используя подстановку , определим комплексный коэффициент передачи

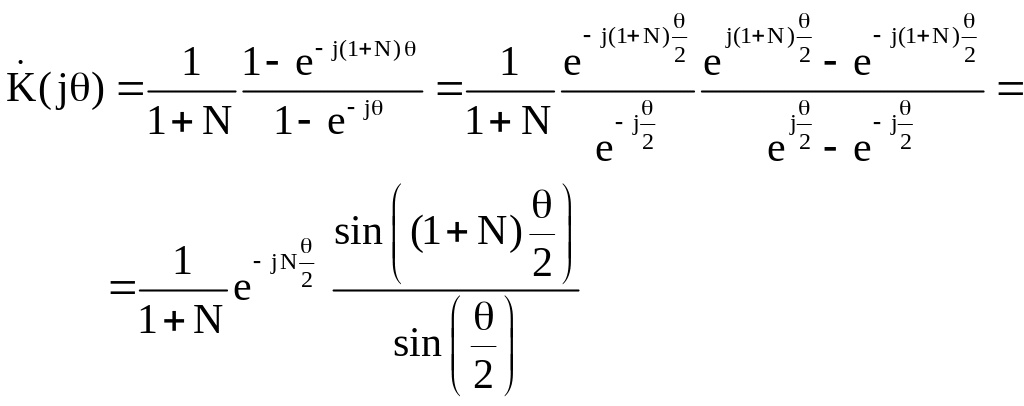(2.19)

Обозначим

. (2.20)

Определим ачх и фчх фильтра

, (2.21)

где

Поскольку ФЧХ принято представлять в интервале значений фазы от –π до π, то соотношение для корректируется путем прибавления или вычитания 2 π

(2.22)

Если после выполнения (2.22) не входит в заданный интервал, то принимают = и вновь выполняют (2.22). Эта операция повторяется до достижения требуемого результата.

Указанная операция автоматически выполняется, например, в программной среде MathCad при определении аргумента комплексного коэффициента передачи.

На рисунке 2.22 приведены АЧХ и ФЧХ однородного фильтра при N=1, а на рисунке 2.23 – функция A(θ), АЧХ и ФЧХ при N=3.

Рисунок 2.22 – АЧХ и ФЧХ однородного фильтра на одном элементе задержки

Рисунок 2.23- Функция A(θ), АЧХ и ФЧХ однородного фильтра при N=3

Из рисунков видно, что однородный фильтр является фильтром нижних частот.

Из сравнения рисунков 2.22 и 2.23 следует, что увеличение длины линии задержки уменьшает полосу пропускания однородного фильтра, а линейная ФЧХ при N=1 превращается в линейно-ломаную при N>1.

2.8. Триангулярный фильтр

Последовательное соединение двух одинаковых однородных фильтров порядка N образует триангулярный фильтр порядка 2N. В качестве примера рассмотрим последовательное соединение двух однородных фильтров второго порядка (рисунок 2.24).

Рисунок 2.24 – Последовательное соединение двух однородных фильтров

Системная функция фильтра определяется соотношением

.

Поскольку коэффициенты системной функции нерекурсивного фильтра являются отсчетами импульсной характеристики фильтра, то из полученного соотношения следует, что импульсная характеристика фильтра симметрична, а ее отсчеты сначала возрастают по линейному закону, а затем убывают также по линейному закону. Схема триангулярного фильтра четвертого порядка приведена на рисунке 2.25 а, а его импульсная характеристика на рисунке 2.25б. Из рисунка видно, что огибающая импульсной характеристики имеет форму равнобедренного треугольника, расположенного на пьедестале – прямоугольнике с высотой B₀ и основанием 2N.

.

Рисунок 2.25– Триангулярный фильтр 4-го порядка

В общем случае триангулярный фильтр порядка 2N описывается следующим разностным уравнением

(2.23)

где

-масштабный коэффициент на входе фильтра, при котором максимальный коэффициент передачи фильтра равен единице (на схеме рисунка 2.25а отсутствует).