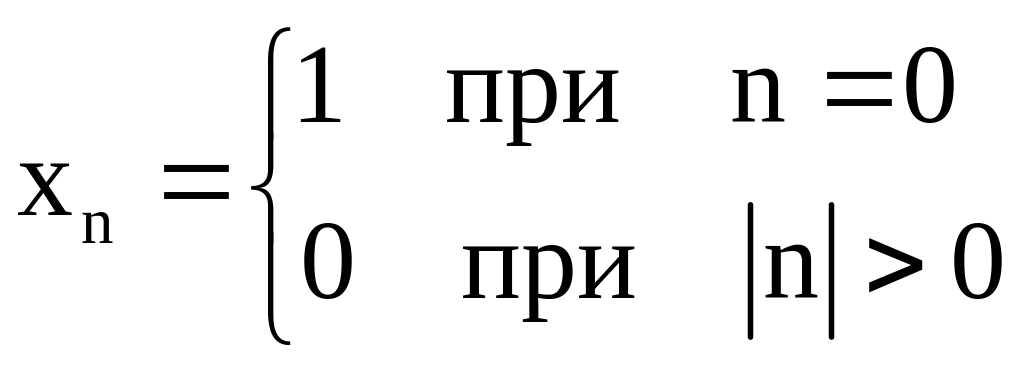2. Цифровые фильтры

Лекция №4

Введение

Фильтрация является одним из видов обработки как аналоговых, так и цифровых сигналов, нашедших широчайшее применение во всех областях деятельности человека.

В телекоммуникационных приложениях фильтрация используется для ограничения спектра сигнала, для селекции сигналов, для режекции помех.

Цифровой фильтр выполняет те же функции, что и аналоговый, но отличается своей реализацией. В данной теме рассматриваются алгоритмы реализации цифровых фильтров, их анализ и синтез.

Математическим аппаратом цифровой фильтрации является Z – преобразование.

Поэтому сначала рассматриваются основные свойства Z - преобразования, основные характеристики цифровых фильтров, а затем вопросы их синтеза.

В данную тему входят следующие разделы:

2.1. Свойства Z-преобразования

2.2. Импульсная характеристика цифрового фильтра. Понятие о рекурсивных и

нерекурсивных цифровых фильтрах, БИХ- и КИХ-фильтрах

2.3. Определение выходного сигнала фильтра по входному сигналу и импульсной

характеристике

2.4. Системная функция цифрового фильтра. Формы программной реализации

Фильтра

2.5. Частотная характеристика цифрового фильтра

2.6. Цифровой резонатор

2.7. Однородный фильтр

2.8. Триангулярный фильтр

2.9. Нерекурсивный фильтр с линейной ФЧХ

2.10. Устойчивость цифровых фильтров

2.11. Коэффициенты системной функции устойчивого звена второго порядка

2.1. Свойства z-преобразования

Прямым Z-преобразованием дискретной последовательности x_n, где n = 0,1, 2.., называется функция комплексной переменной z, определяемая следующим соотношением

. (2.1)

Функция определена для тех значений z, при которых ряд сходится.

Здесь и в дальнейшем последовательность отсчётов обозначается строчной, а ее Z-преобразование той же прописной буквой.

Примеры определения Z-преобразований трех простых последовательностей приведены в таблице 2.1.

Таблица 2.1

Название последовательности	Последовательность	Z-преобразование последовательности
Единичный отсчет		X(z)=1 при
Единичный скачок
Показательная функция

Соотношение (2.1) определяет одностороннее прямое Z – преобразование. Наряду с односторонним существует двухстороннее Z – преобразование, в котором суммирование начинается не от нуля, а от .

Обратное Z – преобразование определяется соотношением

Рассмотрим основные свойства прямого Z-преобразования.

1.Линейность. Пусть последовательность y_n представляет взвешенную сумму двух последовательностей x_1n и x_{2 n}

,

где постоянные весовые коэффициенты.

Тогда Z-преобразование последовательности y_n определяется следующим соотношением

. (2.2)

Таким образом, Z-преобразование взвешенной суммы двух последовательностей равно взвешенной сумме Z-преобразований этих последовательностей.

2.Сдвиг последовательностей. Пусть последовательность y_n представляет собой сдвинутую (задержанную) на m отсчетов последовательность x_n (рисунок 3.1)

.

Тогда Z-преобразование Y(z) последовательности y_n выражается через Z-преобразование X(z) последовательности x_n следующим образом

. (2.3)

Таким образом, Z-преобразование последовательности, сдвинутой относительно исходной на m отсчетов, равно Z-преобразованию исходной последовательности, умноженной на z ^–m.

Рисунок 2.1 – Последовательность y_n сдвинута относительно x_n

на 2 отсчета (2 интервала дискретизации)

3.Дискретная свертка двух последовательностей. Дискретной сверткой двух последовательностей x_n и h_n называется последовательность y_n, определяемая следующим соотношением

. (2.4)

Z-преобразование Y(z) дискретной свертки y_n двух последовательностей равно произведению Z -преобразований H(z) и X(z) исходных последовательностей h_n и x_n

, (2.5)

где .

2.2. Импульсная характеристика цифрового фильтра. Понятие о рекур

сивных и нерекурсивных цифровых фильтрах, БИХ- и КИХ-фильтрах

Цифровым фильтром дискретного сигнала называется линейная частотно-избирательная система, реализуемая на основе вычислительного устройства.

Пусть при действии на входе цифрового фильтра последовательности отсчетов x_n на его выходе действует последовательность y_n .

Если n-ый отсчет выходного сигнала фильтра y_n зависит только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., то такой фильтр называется нерекурсивным.

Если n-ый отсчет выходного сигнала фильтра y_n зависит не только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., но и от отсчетов выходного сигнала в предшествующие моменты времени, то такой фильтр называется рекурсивным.

Импульсной характеристикой цифрового фильтра называется выходной сигнал фильтра при действии на его входе единичного отсчета и нулевых начальных условиях.

На рисунке 2.2 показаны входной сигнал фильтра в виде единичного отсчета x_n и реакция фильтра на этот сигнал – импульсная характеристика h_n.

Фильтр с конечной импульсной характеристикой называется КИХ-фильтром (КИХ-конечная импульсная характеристика). Фильтр с бесконечной импульсной характеристикой называют БИХ-фильтром.

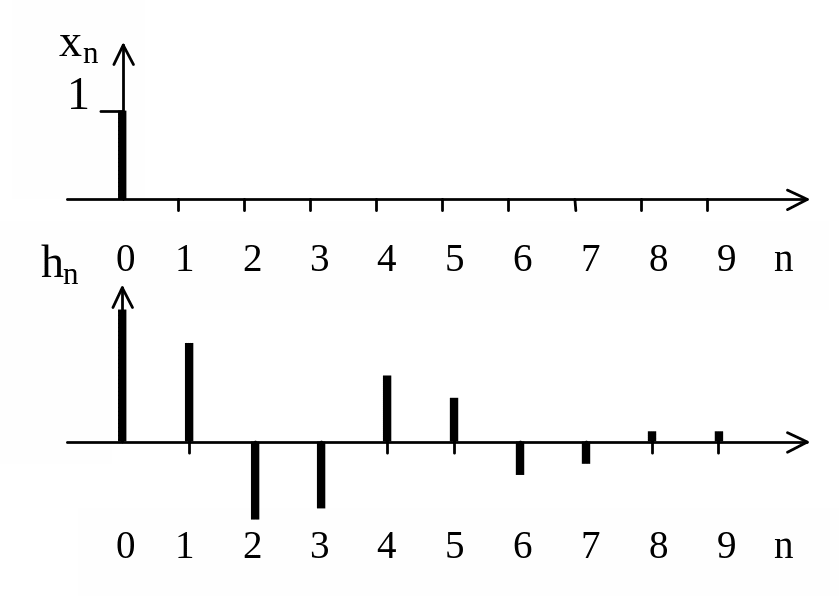
Рисунок 2.2 – Единичный отсчет x_n и импульсная характеристика h_n

2.3. Определение выходного сигнала фильтра по входному сигналу и

импульсной характеристике

Определение выходного сигнала цифрового фильтра по входному сигналу и импульсной характеристике основано на определении импульсной характеристики и принадлежности фильтра к линейным системам, для которых справедлив принцип суперпозиции.

На рисунке 2.3 приведен пример определения выходного сигнала фильтра в случае, когда входной сигнал x_n содержит два отсчета x₀ = 2 и x₁= 2, а импульсная характеристика 3 отсчета: h₀ = 1, h₁=0.5, h₂ = 0.25.

Сначала определим реакцию фильтра на отсчет x₀, считая, что x₁=0. Если бы вместо x₀ действовал единичный отсчет, то выходным сигналом была бы импульсная характеристика.

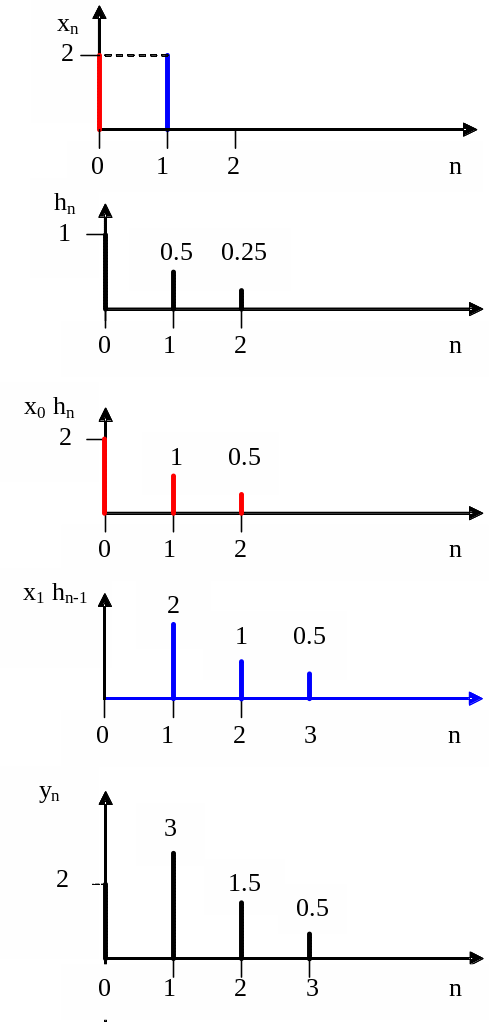
Рисунок 2.3 – Определение выходного сигнала фильтра по входному сигналу и импульсной характеристике

Так как фильтр линейная система, то при входном отсчете в x₀ раз больше единичного, выходной сигнал будет представлять собой импульсную характеристику, все отсчеты которой умножены на x₀, - x₀ h_n.

Определим реакцию фильтра на отсчет сигнала x₁ при x₀ =0. При x₁=1 выходной сигнал фильтра представлял бы собой импульсную характеристику, запаздывающую на один отсчет h_n-1. При отсчете x₁, отличном от единицы, реакцией фильтра будет запаздывающая на один отсчет импульсная характеристика, все отсчеты которой умножены на x₁, - x₁ h_n-1.

Согласно принципу суперпозиции полученные реакции суммируются.

В результате

, , …..

В общем случае

(2.6)

Согласно последнему соотношению

Однако в рассмотренном примере x₂ = 0, поэтому, как видно из рисунка,

В общем случае

В данном примере x₂ = x₃ = 0, h₃ = 0, поэтому

Соотношение 2.6 представляет собой дискретную свертку последовательностей x_n и h_n, т.е. выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра.

На рисунке 2.4 дано графическое представление дискретной свертки при конечной импульсной характеристике фильтра, содержащей N+1 отсчет. Из рисунка видно, что y_n зависит только от отсчетов входного сигнала x_n, x_n-1, .. x_n-N, следовательно, данный фильтр является нерекурсивным.

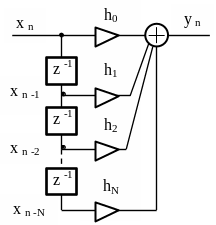
Рисунок 2.4 – Нерекурсивный цифровой фильтр

Лекция №5

2.4. Системная функция цифрового фильтра. Формы программной

реализации фильтра

Системной функцией цифрового фильтра называется отношение Z-преобразования выходного сигнала фильтра к Z-преобразованию входного сигнала

.

Воспользовавшись (2.6) и теоремой о дискретной свертке (раздел 2.1), выразим Z-преобразование Y(z) выходного сигнала фильтра y_n через Z-преобразование X(z) входного сигнала x_n

Y(z) = H(z) X(z),

где .

Из последних соотношений следует, что системная функция H(z) представляет собой Z-преобразование импульсной характеристики цифрового фильтра.

Полюсом системной функции называется значение комплексной переменной z, при котором системная функция H(z) стремится к бесконечности.

Нулем системной функции называется значение комплексной переменной z, при котором системная функция H(z) равна нулю.

Рассмотрим формы программной реализации фильтра:

1. Прямая форма

На рисунке 2.5 представлен алгоритм функционирования цифрового фильтра при прямой форме реализации. Прямая форма следует из определения фильтра как линейной системы. Следовательно, n – ый отсчет выходного сигнала фильтра y_n должен быть связан линейными соотношениями с отсчетами входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1, ..x_n-N и отсчетами выходного сигнала в предшествующие моменты времени y_n-1, y_n-2, .. y_n-N. Соответствующие коэффициенты пропорциональности B₀, B₁, .. B_N, A₁, A₂, .. A_N определяют свойства фильтра.

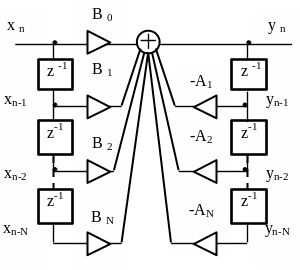
Рисунок 2.5 – Прямая форма программной реализации фильтра

Согласно схеме рисунка 2.5 запишем разностное уравнение

Выразим Z - преобразование выходного сигнала Y(z) через Z-преобразование входного сигнала

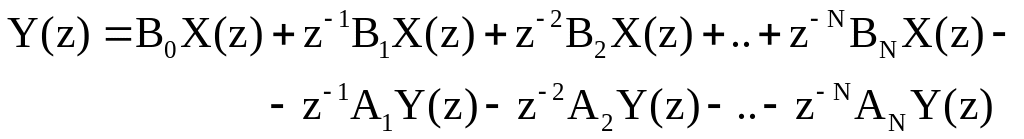
Из последнего соотношения получим

. (2.7)

Таким образом, системная функция цифрового фильтра в общем случае представляет собой дробно-рациональную функцию. Полином числителя описывает нерекурсивную часть фильтра, а полином знаменателя – рекурсивную.

Чтобы найти нули системной функции, нужно полином числителя приравнять нулю и найти корни полученного уравнения.

Чтобы найти полюсы системной функции, нужно полином знаменателя приравнять нулю и найти корни полученного уравнения.

Отметим, что знаки перед коэффициентами A в выражении для системной функции и в разностном уравнении противоположны.

2. Каноническая форма.

Представим выражение (2.7) в виде произведения двух функций

,

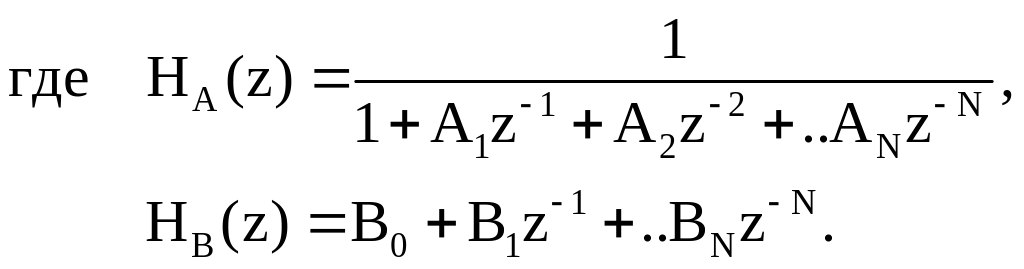(2.8)

Согласно (2.8) цифровой фильтр с системной функцией H(z) можно представить в виде последовательного соединения двух фильтров с системными функциями H_A(z) и H_B(z) (рисунок 2.6).

Рисунок 2.6 – Представление фильтра с прямой формой реализации

в виде последовательного соединения двух фильтров

Действительно,

.

Заменив укрупненный алгоритм рисунка 2.6 детальным, получим схему фильтра, изображенную на рисунке 2.7.

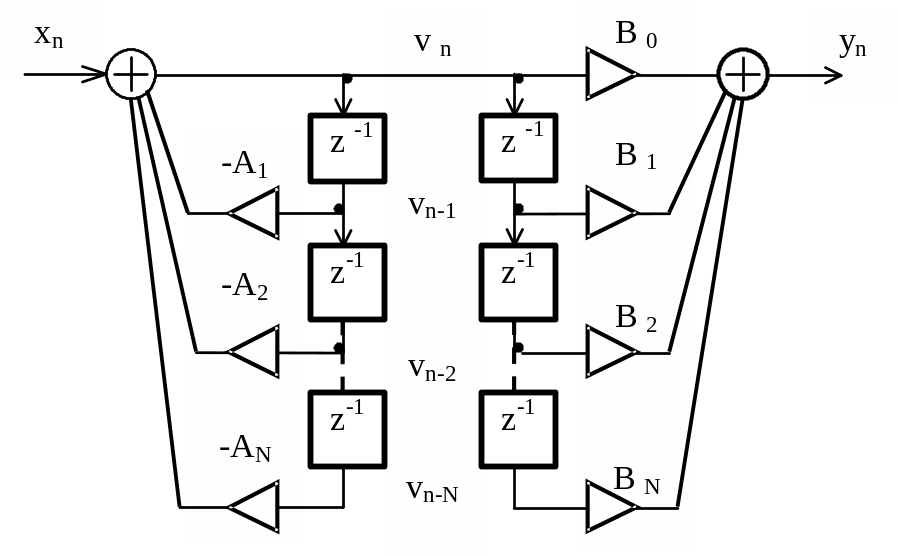
Рисунок 2.7 – Детальный алгоритм представления фильтра с прямой реализацией