Построение графика вдоль пути

General Postproc  Path Operations  Plot Path Item  On Graph. В списке слева (Path items to be graphed) выбрать Stress, справа — компоненту (например, SX) Нажать кнопку OK.

Просмотр и сохранение численных данных.

Перерисовать конечно-элементную сетку или узлы. Для того, чтобы информация выводилась только в нужных узлах, необходимо их выбрать Utility Menu  Select  Entities и выбрать Nodes By Num/Pick , нажать кнопку OK. Мышью выбрать узлы.

Для анализа численной информации и построения графиков в сторонних пакетах можно выводить численные результаты в узлах. General Postproc  List Results  Nodal Solution и в появившемся меню выбрать компоненты вектора перемещений или тензоров напряжений, деформаций. Данные можно сохранить в файле.

Для вывода координат узлов нужно выполнить Utility Menu  List  Nodes, причем их удобно упорядочить по координате. Данные можно сохранить в файле.

3. Задача Ламе

3.1. Введение

Рассматривается бесконечно длинная прямая труба, нагруженная постоянным внутренним давлением p (рис. 3.1). Наружная поверхность трубы свободна от действия нагрузки. Считается, что труба не растягивается вдоль своей оси, то есть находится в условиях плоской деформации. внутренний радиус трубы равен , внешний — . Требуется найти окружные и радиальные напряжения в стенке трубы.

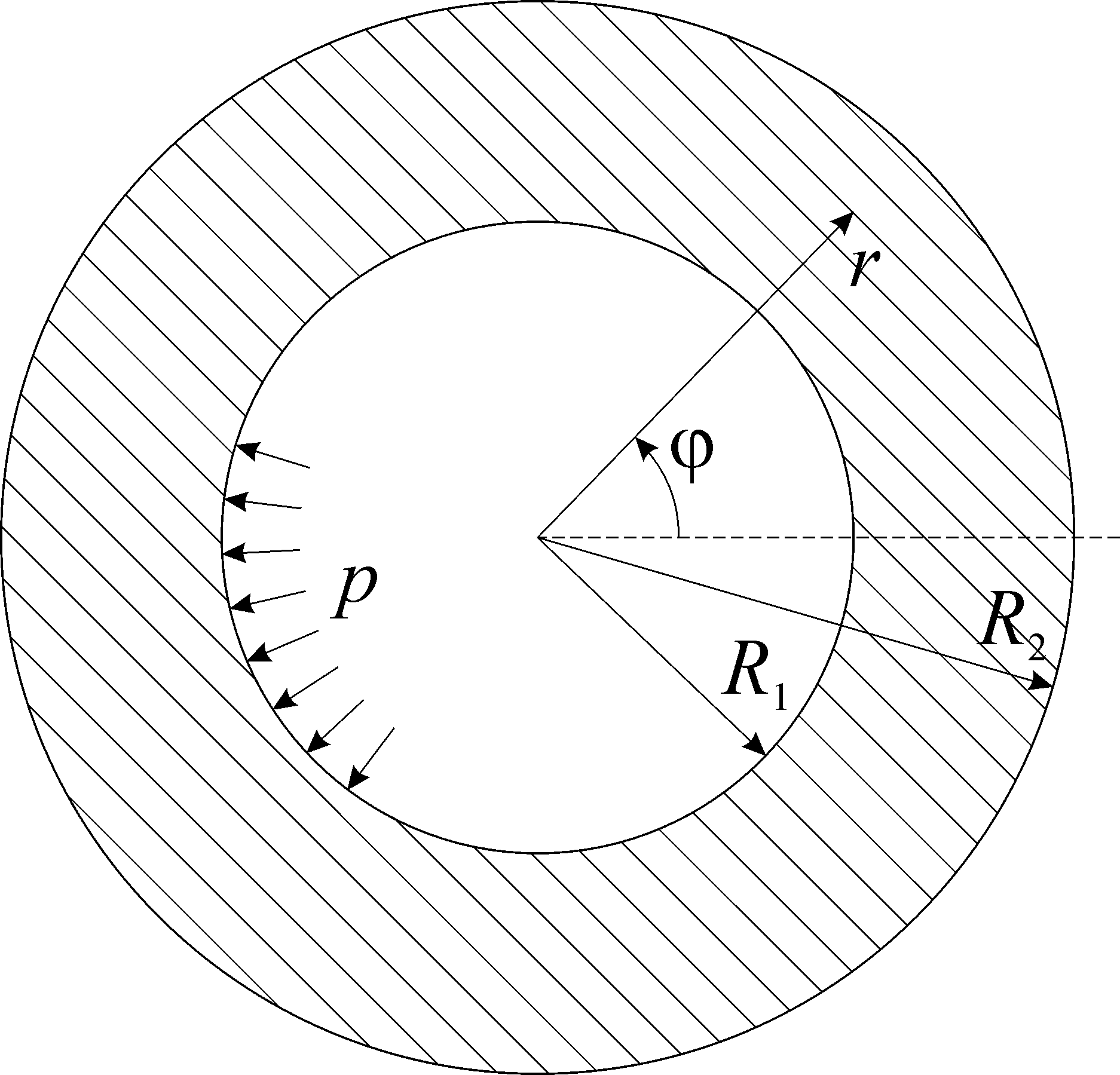
Рис. 3.1: Сечение трубы

Точное решение этой задачи было найдено Г. Ламе. Напряжения (радиальная компонента) и (окружная компонента) определяются по формулам

, (3.1)

Отметим, что при малой толщине h=R₂–R₁ стенки трубы по сравнению с ее средним радиусом R=(R₂+R₁)/2 наиболее опасной становится компонента . В то время как монотонно изменяется от –p на внутренней стенке до нуля на внешней, остается примерно постоянным и имеет значительно большую величину:

(3.2)

3.2. Цели работы

1. Приобрести базовые навыки работы в ANSYS: построение двумерной области; создание равномерных конечно-элементных сеток; задание граничных условий; визуализация и анализ результатов расчета.

2. Исследовать влияние густоты конечно-элементной сетки и порядка аппроксимации конечного элемента на точность численного решения.

3.3. Требования к отчету по работе

В отчете должна быть представлена постановка задачи, сформулированы цели, приведены численные значения всех параметров, описаны варианты расчета. По результатам работы должны быть сделаны выводы (в частности, необходимо объяснить расхождения численных результатов с точным решением).

В работе необходимо решить задачу на четырех разных конечно-элементных сетках:

• На грубой сетке элементов PLANE42

• На мелкой (вдвое мельче) сетке элементов PLANE42

• На грубой сетке (такой же, как в первом варианте) элементов PLANE82

• На мелкой (вдвое мельче) сетке элементов PLANE82

В отчете должны быть представлены графики зависимости радиального и окружного напряжений и (они совпадают с и на линиях =0) для всех расчетов, а также для точного решения. На одном графике можно помещать несколько кривых; лучше всего на одном графике изображать одну компоненту тензора напряжений в разных вариантах расчета и в точном решении.