Шаг 8. Запуск решателя.

По умолчанию ANSYS предполагает, что в задаче рассматривается упругая статика, поэтому никаких предварительных настроек решателя делать не надо. Запуск задачи на счет производится командой Solution  Solve  Current LS. Окно статистики можно закрыть. Если нет сообщений об ошибках, в появляющемся диалоговом окне следует нажать кнопку OK.

Шаг 9. Визуализация и анализ результатов

По окончании расчета результаты анализируются в постпроцессоре (General Postproc). Обычно сразу же после расчета имеет смысл посмотреть вид деформированной области. Для этого используется команда Main Menu  General Postproc  Plot Results  Deformed Shape. В появляющемся диалоге выбирается один из способов отображения исходной области вместе с деформированной (можно выбрать, например, Def + undef edge).

Необходимо вывести картины распределения напряжений и и провести их анализ. Построить средствами ANSYS требуемые графики для визуального сравнения с аналитическими. Для этого сначала создать Путь по оси OX с именем, например, OX и построить графики, затем по оси OY — имя OY. Эти пути пригодятся при решении второй задачи с этой же сеткой.

Шаг 10. Задача растяжения на мелкой сетке.

Задать на линиях в 2 раза большее число элементов, сохранив переменную густоту сетки. Заново разбить поверхность на конечные элементы. Провести расчет и анализ результатов.

Шаг 11. Задача чистого сдвига на мелкой сетке.

Необходимо приложить сжимающее давление на второй стороне области. Затем провести расчет и анализ результатов.

4.5. Параметры задачи

Вариант	1	2	3	4	5	6
Радиус отверстия, м	0.1	0.2	0.25	0.3	0.4	0.5
Длина стороны, м	1	1.5	2	2.5	3.5	4.5

Табл. 4.1: Геометрия области в задаче Кирша

Другие параметры задачи (общие для всех вариантов):

Давление: p = 1000 Па

Материал:

Модуль Юнга: Е = 210¹¹ Па

Коэффициент Пуассона: = 0.3

Параметры КЭ сетки:

Используемый элемент: PLANE82

Для грубой сетки дуга окружности содержит 4-5 элементов, стороны квадрата–10 элементов, оси симметрии–15. Параметр сгущения на осях симметрии 3 (или 0.333 — это зависит от направления обхода стороны и определяется экспериментально).

5. Контактная задача Герца

5.1.Введение

Рассматривается задача о соприкосновении упругого шара с абсолютно твердой плоскостью. Шар радиуса R прижимается к плоскости силой P (рис. 5.1).

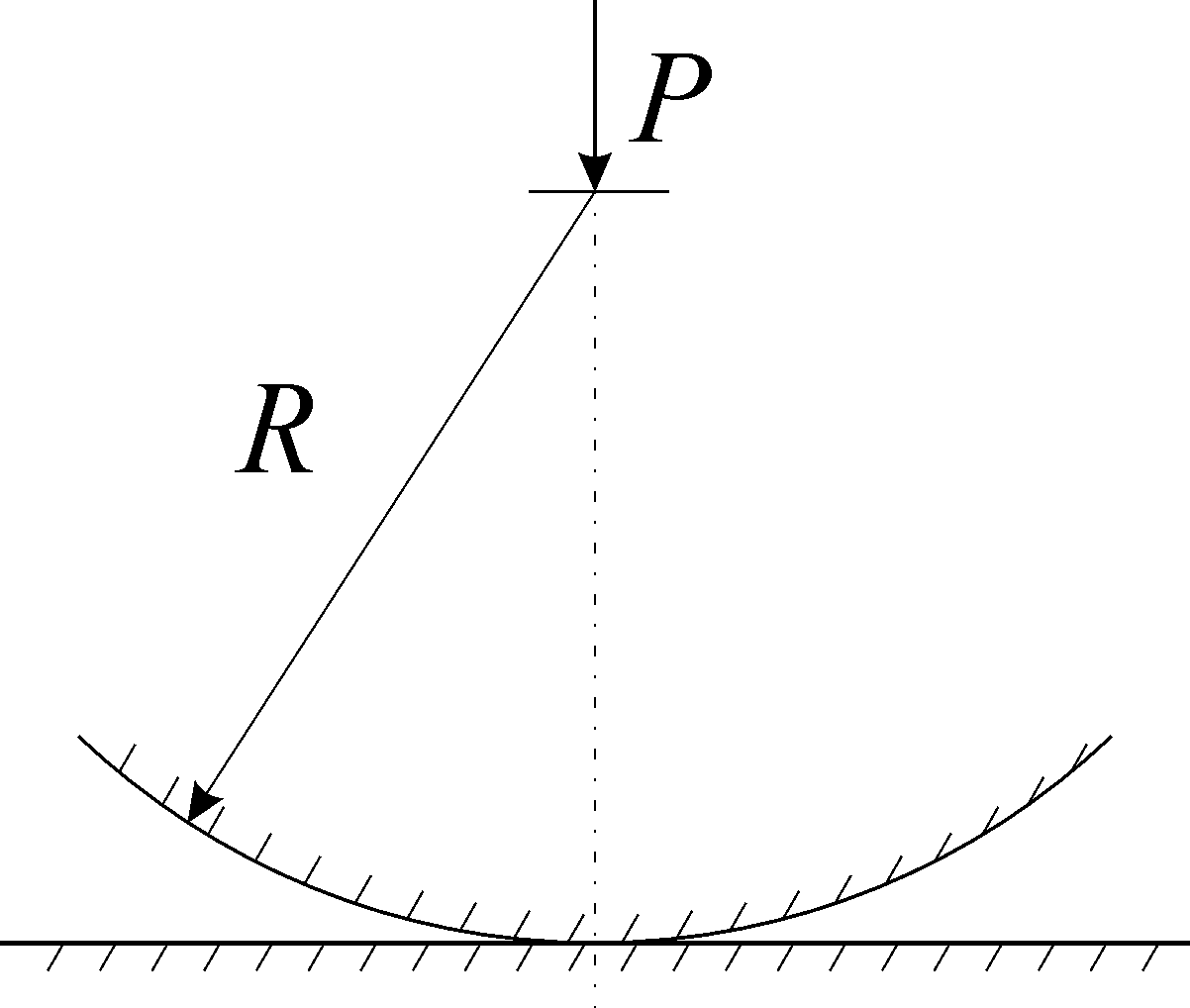
Рис. 5.1. Контакт упругого шара с абсолютно твердой плоскостью

На поверхности контакта отсутствует трение, то есть силы реакции, действующие на шар со стороны плоскости, направлены по нормали к ней. Предметом анализа является напряженно-деформированное состояние шара вблизи зоны контакта. В частности, представляют интерес радиус круга контакта a; максимальное давление p_max на поверхности контакта; перемещения u точек шара, удаленных от зоны контакта, в зависимости от прижимающей силы (перемещения этих точек примерно одинаковы, так как вдали от зоны контакта шар практически не деформируется). Данная задача в более общей постановке была решена Герцем (он рассматривал контакт двух шаров разных радиусов). В рассматриваемом здесь случае формулы, полученные Герцем для интересующих нас величин, принимают следующий вид:

, , (5.1)

Здесь E — модуль Юнга материала шара; коэффициент Пуассона в этих формулах принят равным 0.3.