Министерство образования РФ

СЕВМАШВТУЗ

Кафедра №6.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

По выполнению лабораторной работы №

«Исследование работы системы фазового управления тиристорного регулятора»

по дисциплине «Полупроводниковые преобразователи»

Индекс в соответствии с У.П.2000 г. Количество часов – 2 часа

ДС 05 специальность 140400

Северодвинск

2001

1

ИССЛЕДОВАНИЕ РАБОТЫ СИСТЕМЫ ФАЗОВОГО УПРАВЛЕНИЯ ТИРИСТОРНОГО РЕГУЛЯТОРА

1. ЦЕЛЬ РАБОТЫ.

Изучение работы системы фазового управления тиристорного регулятора

2. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ.

2.1 Сравнение способов регулирования по содержанию гармоник и уровню помех.

Схемы регулятора переменного тока, временные диаграммы токов или напряжений при фазовом и импульсном регулировании идентичны и представлены на рис. 1

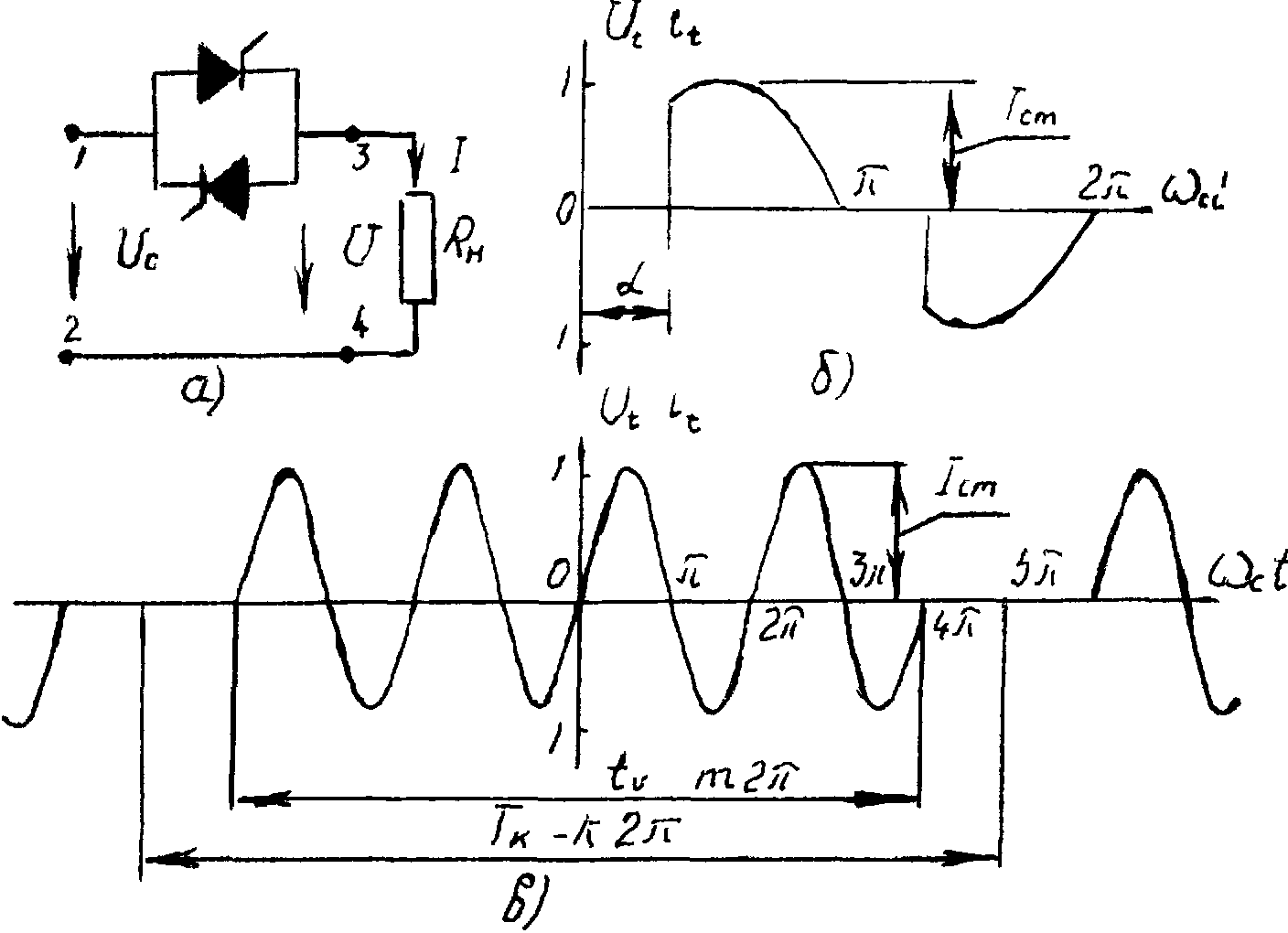
Рис 1

При фазовом регулировании диаграмма тока нагрузки (рис.1.2) может быть представлена как периодическая функция времени с периодом Т=2, симметричная относительно оси абсцисс. Разложение такой кривой в ряд Фурье содержит только нечетные гармоники.

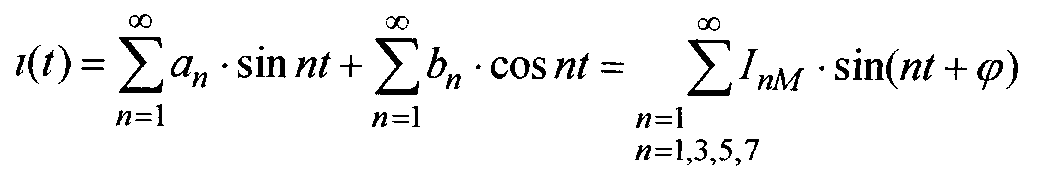
Если функция симметрична относительно какой-либо оси или начала координат, то достаточно знать её аналитическое выражение за половину периода

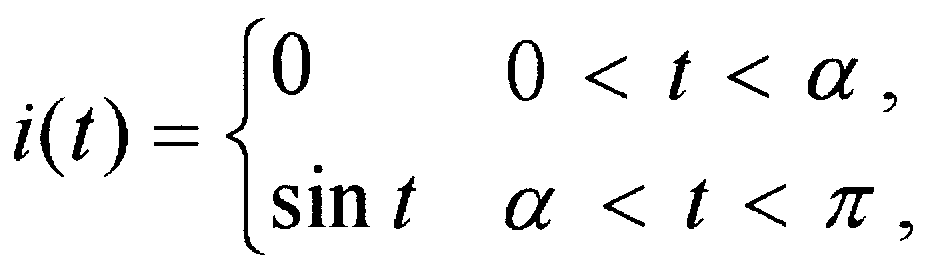
чтобы определить коэффициенты ряда Фурье:

2

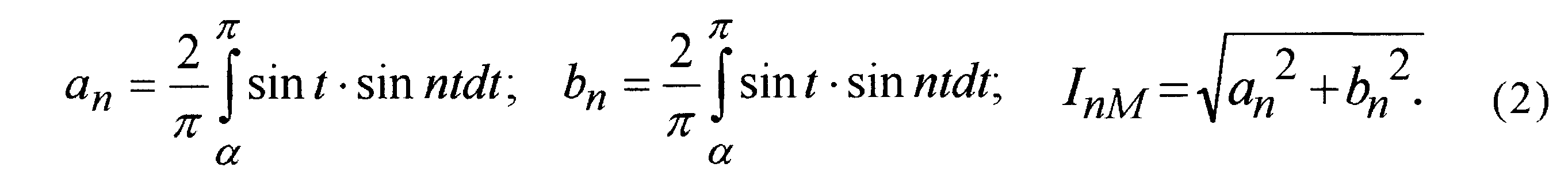
Согласно (2) амплитуда первой гармоники I1M, амплитуды её активной I1aM и реактивной I1pM составляющих, а также косинуса угла сдвига по фазе между первыми гармониками тока и напряжения cos1 можно найти, как

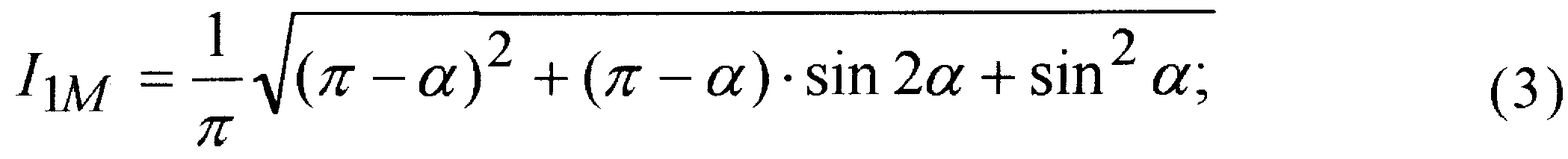
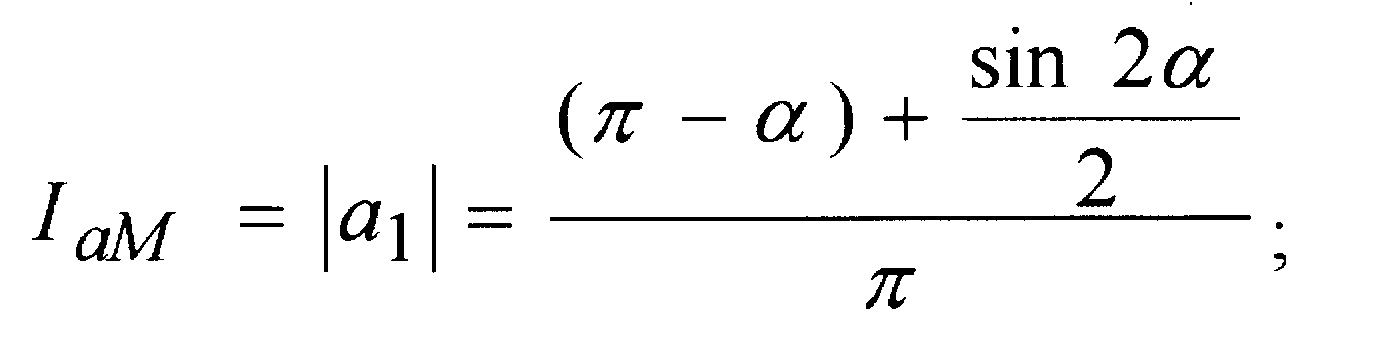
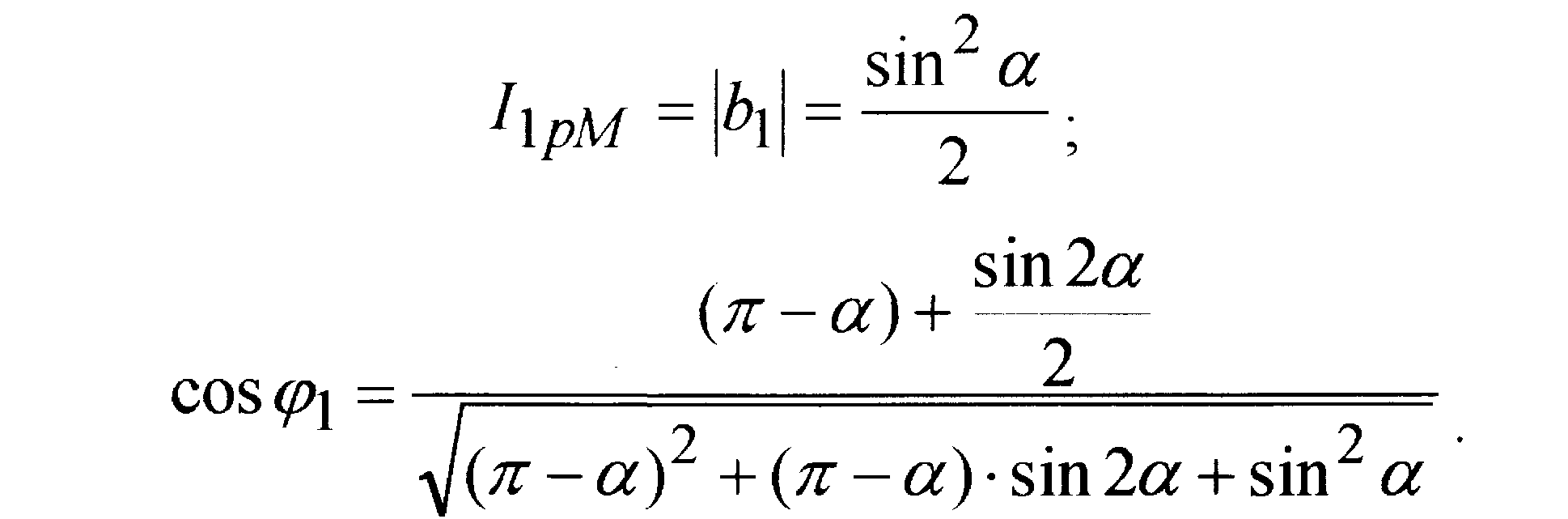
Амплитуда п-й гармоники согласно (2) может быть найдена, как

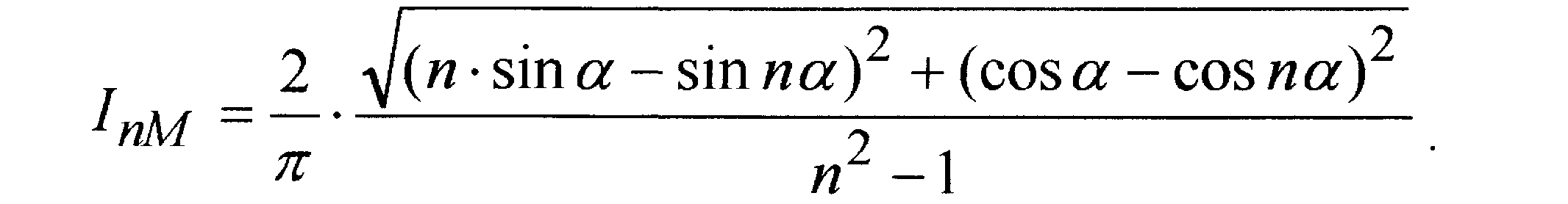
При достаточно больших значениях порядкового номера гармоник n, можно перейти к приближённому выражению вычисления и? действующих значений:

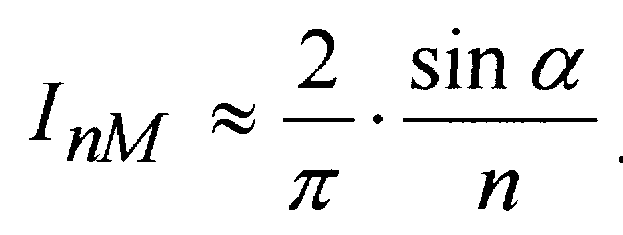
Для ограничения скорости нарастания тока при фазового регулировании в цепь нагрузки часто вводят линейный или насыщающийся дроссель. Введение дросселя меняет диаграмму тока, но практически не изменяет временную диаграмму суммарного напряжения на дросселе и нагрузке, а следовательно, и спектр гармоник напряжения. Сопротивление нагрузки n-й гармонике тока при линейном дросселе может быть найдено как:

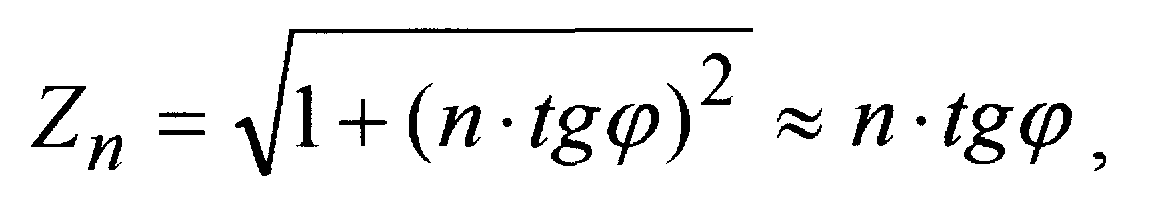
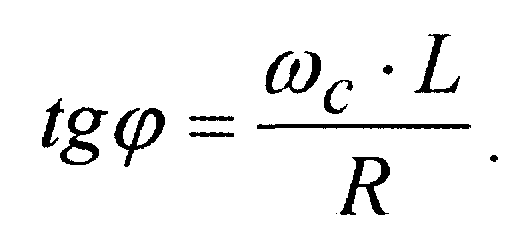
где

3

Амплитуды гармоник тока высокого порядка при наличии дросселя можно определить следующим образом:

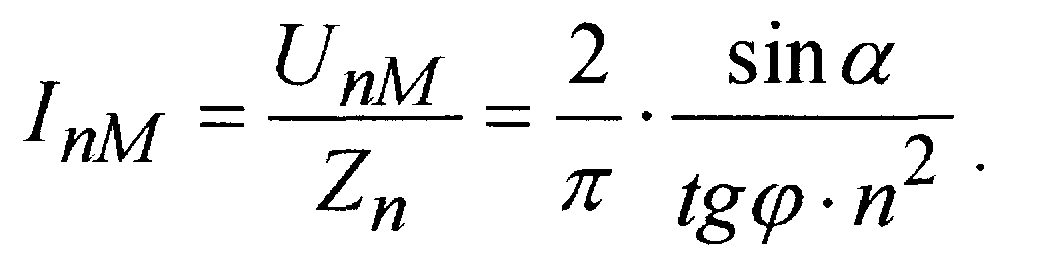
В случае применения насыщающегося дросселя расчёт спектра гармоник высокого порядка более сложен. Приближённо можно считать в этом случае, что tg  определяется величиной индуктивности насыщенного дросселя.

При импульсном регулировании диаграмма тока нагрузки (рис.1.3) есть периодическая функция времени с периодом T=k •2, симметричная относительно начала координат, или нечётная функция. Такие функции раскладываются в ряд Фурье только по синусам. Для сравнения импульсного и фазового регулирования удобно номер гармоники характеризовать числом, величина которого является относительной частотой гармоники. Для фазового регулирования это будет величина n, для импульсного – n/k.

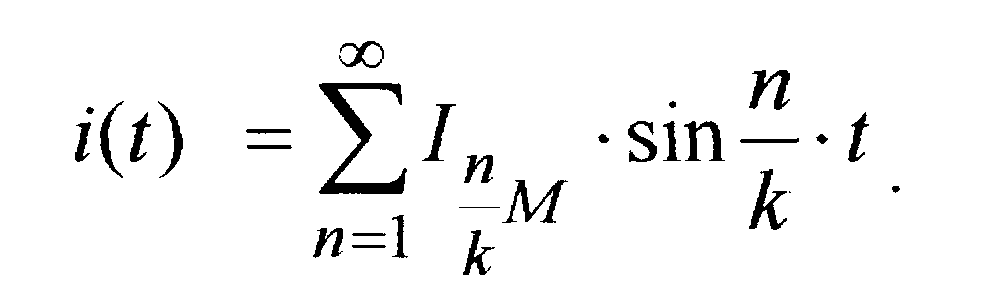
Из этого выражения следует, что фазы всех гармоник в начале координат (рис.1.3) равны либо нулю, либо "" и в токе нагрузки отсутствует реактивная составляющая 1-й гармоники (cos1=l). Мгновенное значение тока аналитически может быть записано в следующем виде:

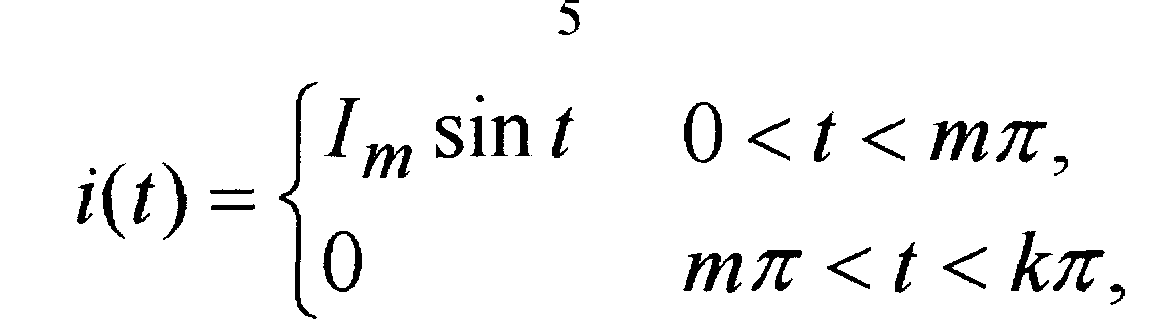
где m - число импульсов в пачке (tu=2m).

Амплитуда гармоники

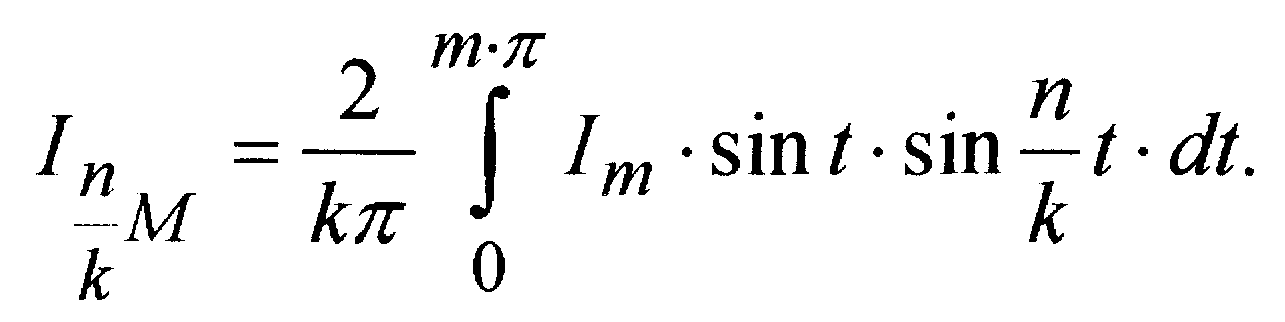
После преобразований можно получить выражение для амплитуды n/k-й гармоники тока через период включений Т_k= 2k и глубину импульсного регулирования "  "

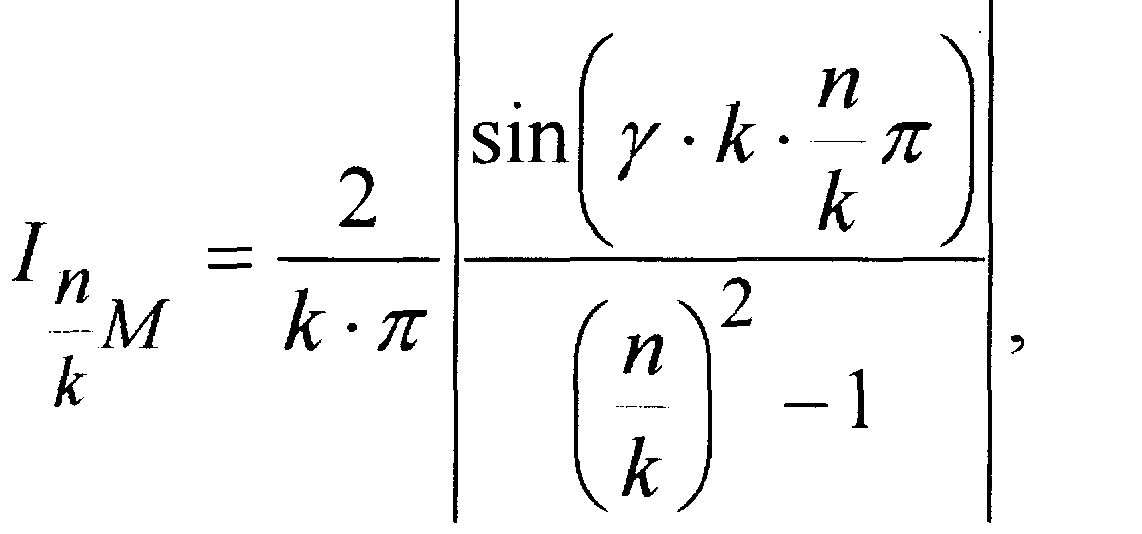
4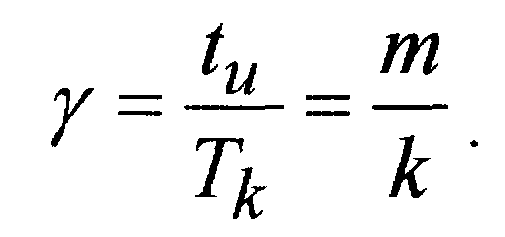

где

Амплитуда первой гармоники и её активная составляющая (cos1 =1) после раскрытия неопределённости

Гармоники высоких порядков при (n/k)²>>1 можно находить по упрощённой формуле

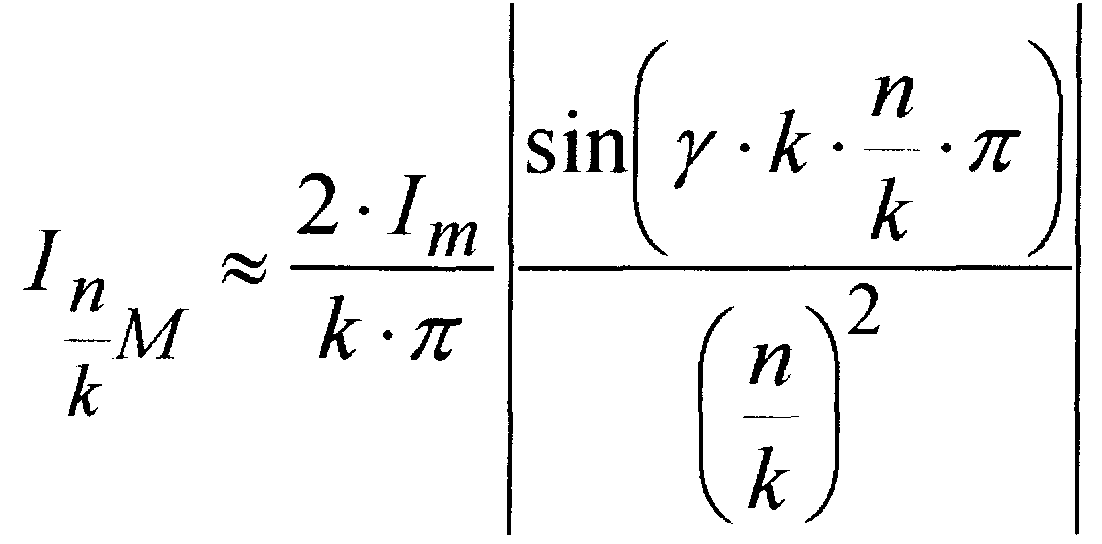
Амплитудный спектр гармоник тока при фазовом и импульсном регулировании представлен на рис 2. 1 и 2. 2 соответственно.

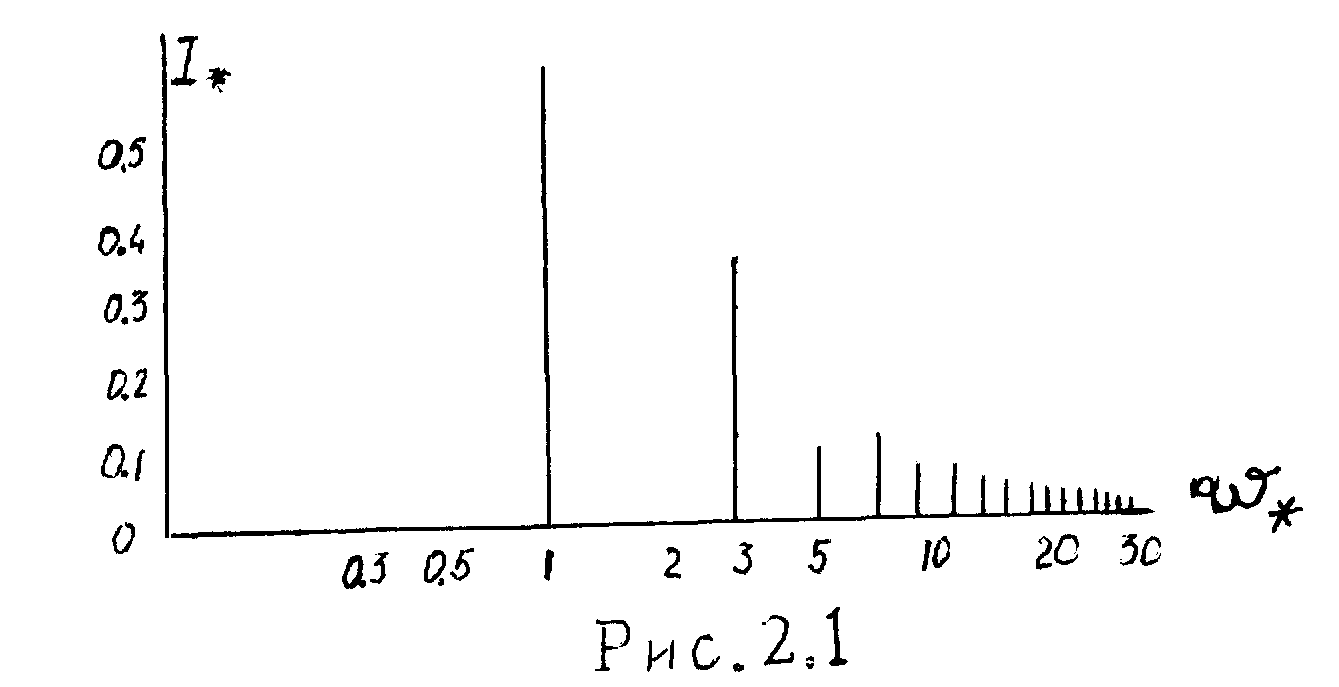
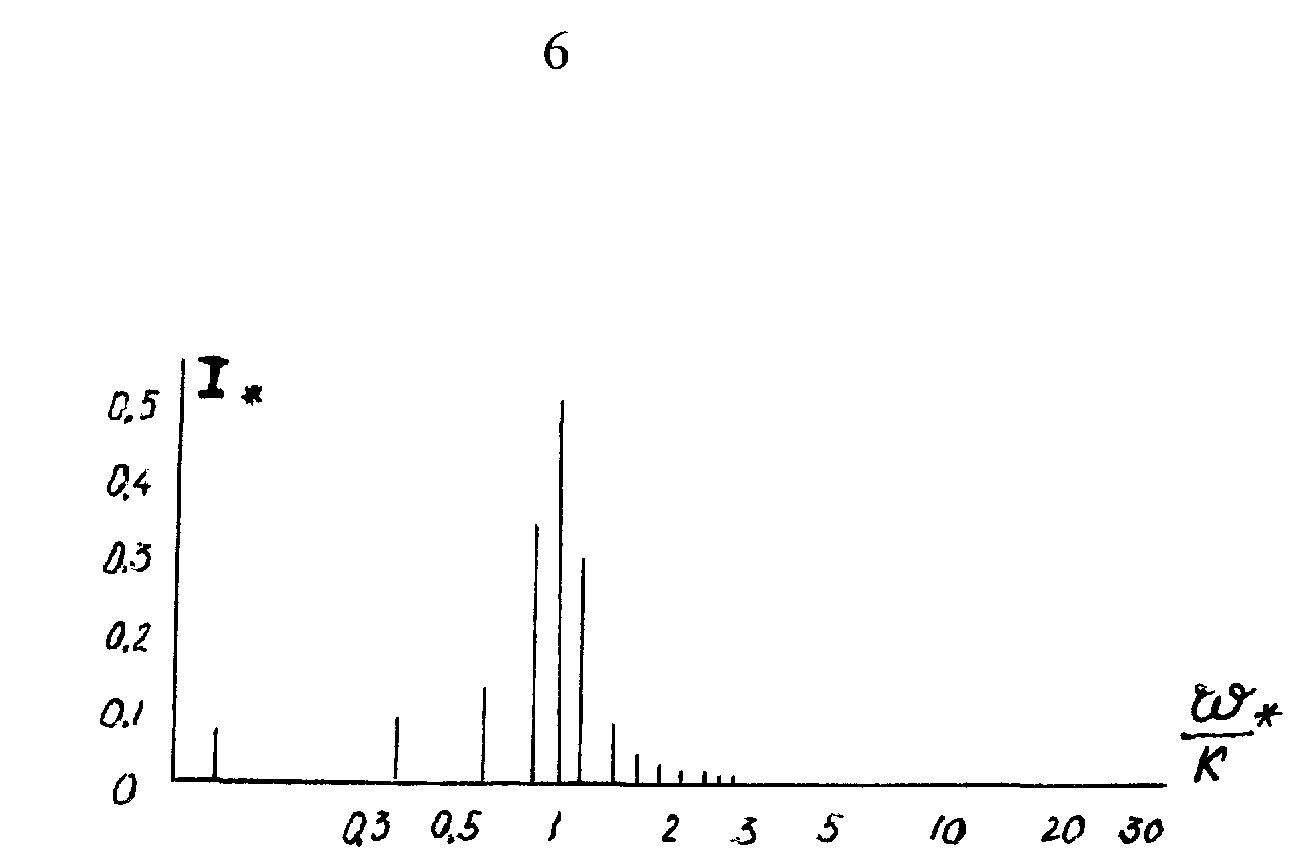
Рис. 2. 2

Особенностью импульсного регулирования является появление в спектре тока гармоник ниже частоты сети и в диапазоне 1 и 2-ой гармоник частоты сети, которые несут практически всю энергию, передаваемую из сети к нагрузке.

При импульсном регулировании в спектре высших гармоник отсутствуют

5

гармоники, кратные частоте сети n = 2, 3, 4, 5..., так как sin(*k*n/k*) = 0. Гармоники, кратные частоте сети, искажают форму синусоиды напряжения сети, что имеет место при фазовом регулировании. Импульсное регулирование почти не искажает форму синусоиды, но низкочастотные гармоники приводят к возбуждению низкочастотных колебаний напряжения сети.