Симплекс-метод решения задач линейного программирования.
Рассмотренный ранее графический метод позволяет находить оптимальные значения целевой функции на плоскости, т.е. когда в системе ограничений стандартной задачи ЛП даны лишь две переменных – и .
Симплекс-метод является универсальным методом, который позволяет находить оптимальные значения при большом количестве переменных.
Суть симплекс-метода состоит в таком целенаправленном переборе возможных вариантов решения, при котором каждое последующее решение лучше, чем предыдущее.
Алгоритм симплекс-метода.
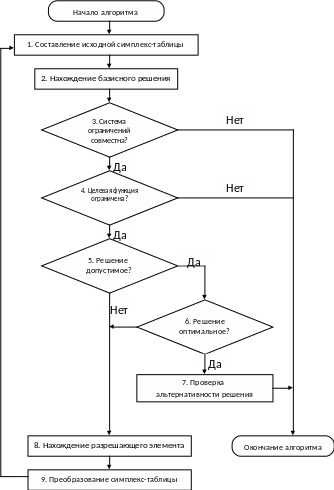
1 Этап. Составление исходной симплекс-таблицы.
Исходную
задачу линейного программирования
необходимо привести к канонической
форме и преобразовать к следующему
виду, выбрав при этом в качестве базисных
переменных дополнительные переменные
,
,
…, 
:
На основе преобразованной канонической задачи составляем исходную симплекс-таблицу (данные берем без раскрытия скобок):
Базисные переменные |
Свободные
члены |
Свободные переменные |
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример:
Путем введения дополнительных неотрицательных переменных со знаком «+» в полученную систему ограничений, задача ЛП приводиться к каноническому виду:
;
;
;
;
.
Далее выражаем данные дополнительные переменные через свободные:
; ; ; ; .
На основе полученной задачи составляем исходную симплекс-таблицу (данные берем без раскрытия скобок):
Базисные переменные |
Свободные члены |
Свободные переменные |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Любые m переменных системы ограничений ЗЛП в каноническом виде, состоящей из m-линейно-независимых уравнений с n переменными (m<n), называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n–m переменных называются неосновными (или свободными).
2 Этап. Нахождение базисного решения.
Решение, при котором все свободные переменные равны нулю, называется базисным решением. Базисное решение легко определить по симплекс-таблице. Так, первый столбец симплекс-таблицы показывает базисные переменные, вторая – соответствующие им значения. Свободные переменные приравниваются к нулю.
В нашем примере:
– базисное решение.