Лекции по дисциплине «Математические методы в экономике»

Разработал к.э.н., доцент Казанского Федерального Университета Карамышев Антон Николаевич

Введение

На практике часто возникают задачи, в которых необходимо найти максимальную прибыль или минимальную стоимость при наличии некоторых материальных, трудовых, временных, финансовых ограничений.

С математической точки зрения выше написанное означает нахождение максимума или минимума некоторой целевой функции от многих переменных, когда на эти переменные накладываются определенные ограничения.

Дисциплина, изучающая такие задачи и разрабатывающая методы их решения, называется «Математические методы в экономике».

Задачи линейного программирования.

В общем виде задача ЛП выглядит так:

где , , - заданные постоянные величины (числа).

Функцию (1) называют целевой функцией;

системы (2) и (3) – системой ограничений;

условие (4) – условием неотрицательности проектных параметров.

Совокупность проектных параметров 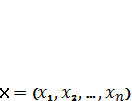удовлетворяющих ограничениям (2), (3) и условию (4) называют допустимым решением или планом.

Допустимое решение , при котором целевая функция принимает оптимальное (максимальное или минимальное) значение, называется оптимальным решением или оптимальным планом задачи ЛП.

Стандартная задача ЛП имеет следующий вид:

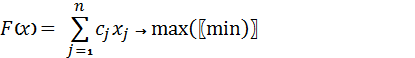
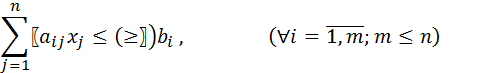
Каноническая задача ЛП имеет следующий вид:

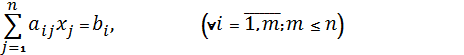
Все три формы задачи ЛП эквивалентны, т.к. каждая из них с помощью некоторых преобразований может быть переписана в другую форму.

Для преобразования ограничения-неравенства в ограничение-равенство вводят дополнительную неотрицательную переменную:

а) со знаком «–», если неравенство «≥»;

б) со знаком «+», если неравенство «≤».

Для преобразования ограничения-равенства в ограничение-неравенство выражают одну из неотрицательных переменных через остальные, а затем исключают ее с переходом к неравенству.

Выделяют следующие задачи ЛП:

1. Задача об использовании ресурсов (задача планирования производства);

2. Задача составления рациона (задача о диете, задача о смесях);

3. Задача об использовании мощностей (задача о загрузке оборудования);

4. Задача о раскрое материалов;

5. Транспортная задача.

Примеры составления задач лп.

1. Задача планирования производства.

Для изготовления двух видов продукции используем четыре вида ресурсов . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1.

Таблица 1

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
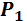
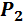
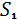
	18	1	3
	16	2	1
	5	-	1
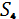
	21	3	-

Прибыль от реализации продукции , Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение: составим экономико-математическую модель задачи.

Для их изготовления потребуется ресурсов:

При этом объем потребляемых ресурсов не должен превышать их запасы, т.е. имеются следующие ограничения.

По смыслу задачи переменные и должны быть неотрицательные, т.е.

, ≥ 0.

Суммарная прибыль от реализации продукции составит:

Обобщим задачу планирования производства.

Пусть планируется произвести n видов продукции из m видов ресурсов.

– виды производимой продукции;

– число единиц продукции , запланированное к производству;

– виды потребляемых ресурсов;

– запас ресурса ;

- число единиц ресурса , затрачиваемого на изготовление единицы продукции ;

– прибыль от реализации единицы продукции .

Экономико-математическая модель задачи планирования производства в общей постановке примет вид: найти такой план выпуска продукции, удовлетворяющий системе:

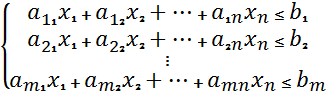(1)

и условию (2)

при котором функция принимает максимальное значение.