Историческая формулировка

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Интересно, что если добавить требование инерциальной системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой  , а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Современная формулировка

Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

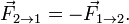
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Историческая формулировка

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[2].

Формула Циолковского

[править]

Материал из Википедии — свободной энциклопедии

Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.

,

где:

 — конечная (после выработки всего топлива) скорость летательного аппарата;

 — удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива);

 — начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо).

 — конечная масса летательного аппарата (полезная нагрузка + конструкция);

Эта формула была выведена К. Э. Циолковским в рукописи «Ракета» 10 мая 1897 года (22 мая по григорианскому календарю).^[1]

Однако первыми уравнение движения тела с переменной массой решили английские исследователи У. Мур, а также П. Г. Тэйт и У. Дж. Стил изКембриджского университета соответственно в 1810—1811 гг. и в 1856 году.

Формула Циолковского может быть получена путём интегрирования дифференциального уравнения Мещерского для материальной точки переменноймассы:

,

в котором   — масса точки;

 — скорость точки;

 — относительная скорость, с которой движется отделяющаяся от точки часть её массы. Для ракетного двигателя эта величина и составляет егоудельный импульс  ^[2]

Для многоступенчатой ракеты конечная скорость рассчитывается как сумма скоростей, полученных по формуле Циолковского отдельно для каждой ступени, причем при расчёте характеристической скорости каждой ступени к её начальной и конечной массе добавляется суммарная начальная масса всех последующих ступеней.

Введем обозначения:

 — масса заправленной  -ой ступени ракеты;

 — масса  -ой ступени без топлива;

 — удельный импульс двигателя  -ой ступени;

 — масса полезной нагрузки;

 — число ступеней ракеты.

Тогда формула Циолковского для многоступенчатой ракеты может быть записана в следующем виде:

4)

Динамика вращательного движения. Основные понятия: момент силы, момент инерции, момент импульса. Основное уравнения динамики вращательного движения. Закон сохранения момента импульса и его применение.