Невырожденные матрицы. Обратная матрица.

Пусть А – квадратная матрица n-го порядка

А= .

Квадратная матрица А называется невырожденной, если определитель не равен нулю, в противном случае ( ) матрица А называется вырожденной.

Матрицей, союзной к матрице А, называется матрица

А =

где А - алгебраическое дополнение элемента данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).

Обратная матрица

Понятие обратной матрицы вводится только для квадратной матрицы.

Матрица называется обратной матрице А, если выполняется условие

,

где Е – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.

Теорема1: Всякая невырожденная матрица имеет обратную.

Теорема2: Матрица где А - алгебраическое дополнение элемента невырожденной матрицы А, является обратной для матрицы А.

Алгоритм нахождения обратной матрицы.

1. Найти определитель матрицы А.

2. Найти алгебраические дополнения А всех элементов матрицы А и составить матрицу А , элементами которой являются алгебраические дополнения А .

3. Найти матрицу, транспонированную полученной матрице А , и умножить её на - это и будет = .

4. Сделать проверку: .

Свойства обратной матрицы.

1.

2.

3.

Пример 6: Найти обратную матрицу для матрицы А и сделать проверку.

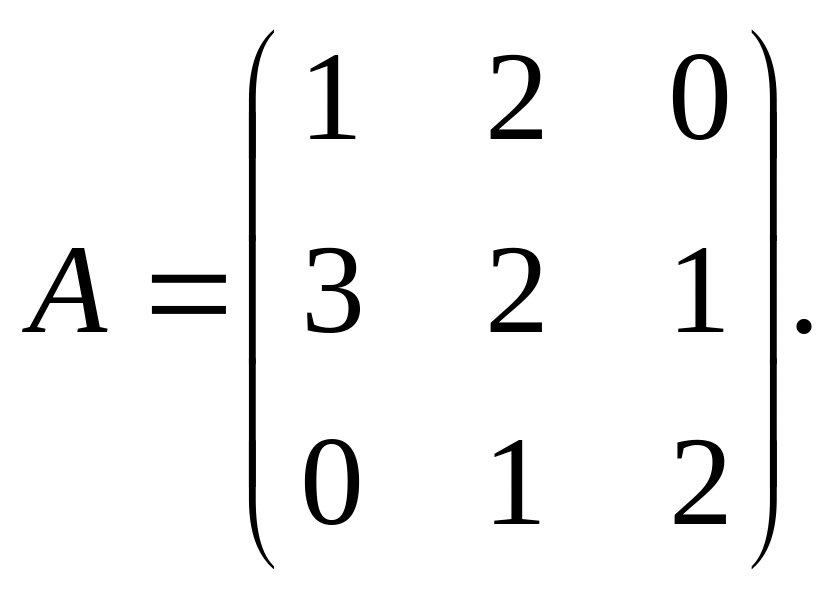
Определитель , следовательно матрица А невырожденная и обратная для неё матрица существует.

Составляем матрицу .

.

Отсюда, матрица

Проверка:

Ранг матрицы.

1. Вычисление ранга по определению.

Пусть дана матрица А размера

А= .

В матрице А размера вычёркиванием каких – либо строк и столбцов можно выделить квадратные подматрицы к-го порядка, где Определители таких подматриц называются минорами к-го порядка матрицы А.

Например, из матрицы можно получить подматрицы первого, второго и третьего порядков.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

Ранг матрицы А обозначается: rang A, или r(A).

Из определения следует:

• ранг матрицы не превосходит меньшего из её размеров, т.е.

• r(A)=0тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А нулевая матрица;

• для квадратной матрицы n-го порядка r(A)= n тогда и только тогда, когда матрица А – невырожденная.

Пример 7 :Вычислить ранг матрицы

Матрица А имеет четвёртый порядок, поэтому . Однако , так как матрица А содержит нулевой столбец, поэтому .Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители, значит Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвёртый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом Поскольку матрица А содержит не нулевые элементы, т.е. невырожденные подматрицы первого порядка, то .

Пример 8: Вычислить ранг матрицы

Для матрицы

Проверим равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычёркивании одного из столбцов матрицы):

Поскольку все миноры третьего порядка нулевые, Так как существует не нулевой минор второго порядка, например,

то

В общем случае определение ранга матрицы перебором всех миноров достаточно трудоёмко. Для облегчения этой задачи используют преобразования, сохраняющие ранг матрицы.

Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Обозначается А~В.

Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.