Раздел X. Дифференциальные уравнения

До сих пор нам встречались только числовые уравнения. Они так называются потому, что решением их являются некоторые числа. Например, решениями квадратного уравнения являются 2 числа: и . Однако при изучении явлений природы в различных областях знаний интерес представляет, например, нахождение закона развития некоторого явления с течением времени (т.е. зависимость параметров, описывающих явление, от времени t), либо характер зависимости одних параметров явления от других его параметров. Такие закономерности уже описываются некоторой функцией. Поэтому для выяснения закономерностей развития некоторого явления необходимо найти соответствующую функцию. Уравнение, в котором в качестве неизвестного, подлежащего определению, выступает некоторая функция, называется функциональным уравнением. Мы будем рассматривать частный вид функциональных уравнений, которые называются обыкновенными дифференциальными уравнениями.

Обыкновенным дифференциальным уравнением (далее − просто дифференциальным уравнением) называется функциональное уравнение, связывающее искомую функцию и ее производные до некоторого порядка , , ... , . Порядком дифференциального уравнения называется порядок наивысшей входящей в него производной от искомой функции.

Пример. − дифференциальное уравнение 3 порядка.

Очень многие законы природы в различных областях описываются дифференциальными уравнениями. Это и механическое движение тел по законам Ньютона, модель естественного роста выпуска продукции, модель рынка с прогнозируемыми ценами, законы нагревания и остывания тел, законы колебаний систем, процесс радиоактивного распада, процесс размножения бактерий и многое другое.

Дифференциальные уравнения первого порядка

Это дифференциальные уравнения на неизвестную функцию , куда могут входить аргумент искомой функции, сама искомая функция и ее первая производная . Мы будем сначала рассматривать уравнения, разрешенные относительно этой производной, т.е. уравнения вида

(1) .

Справа в (1) может быть любая функция (чаще всего – формула) от двух переменных и .

Что мы будем называть решением такого уравнения? Решением числового уравнения, как известно, называется такое число, подстановка которого в уравнение вместо неизвестного превращает его в верное числовое равенство. Аналогично, функция называется решением уравнения (1) на некотором числовом интервале , если при подстановке ее в уравнение вместо неизвестной функции получается верное тождество на этом интервале: . Если функция является решением уравнения , то ее график называется интегральной кривой этого уравнения.

Пример 1. При каком значении параметра функция является на области своего определения решением уравнения ?

Решение. По определению решения, функция является решением уравнения , если при ее подстановке в уравнение получается верное тождество. Перед такой подстановкой требуется вычислить производную этой функции, так как левая часть уравнения требует подстановки не самой проверяемой функции, а ее производной. Поскольку , то после указанной подстановки получаем: или . Понятно, что последнее равенство становится тождеством только при . Таким образом, функция является решением уравнения только при .

Рассмотрим теперь уравнение

(2) .

В данном примере правая часть уравнения (1) имеет вид . Убедимся, что функция является его решением (на любом интервале, не содержащем 0). Для этого подставим ее в правую и левую часть уравнения (2) и убедимся, что получается верное тождество: , что после вычисления производной и сокращения в правой части действительно дает тождество . Есть ли другие решения этого уравнения? Другими словами, есть ли другие функции, обращающие уравнение (2) в верное тождество? Легко понять, что в решении этого уравнения двойку можно заменить на любое другое число, при этом функция опять будет решением уравнения (2). Убедимся, что какое бы число мы ни взяли, функция является решением этого уравнения (а не только при , что мы только что проверили). Подставляя функцию при произвольном числе в уравнение (2), получаем: , , − верное тождество (каким бы числом ни было). Поэтому решением уравнения (2) является функция при любом числе . Таким образом, решений у этого уравнения бесконечно много. При этом бесконечность множества решений обусловлена тем, что в формулу для решения входит так называемая произвольная постоянная , которой можно придавать любое числовое значение, получая при этом снова решения уравнения. Для такой формулы есть соответствующий термин. Выражение вида (справа стоит формула, содержащая и ) называется общим решением уравнения , если при подстановке в это выражение вместо любого (допустимого) числа будем получать решение этого уравнения. Все получающиеся при этом решения уравнения (1) называются его частными решениями. Все ли решения уравнения содержатся в его общем решении? Ответ зависит от уравнения. Особым решением дифференциального уравнения (1) называется такое его решение, которое не получается из его общего решения ни при каком значении . Для уравнения , как мы только что выяснили, общим решением будет . Нахождение общего решения дифференциального уравнения и его особых решений является конечной целью его исследования. Но в процессе решения дифференциального уравнения мы обычно получаем не сразу общее решение вида (в котором явно выражена переменная от и ), а некоторое соотношение, связывающее , и . Такое соотношение называется общим интегралом дифференциального уравнения. Если затем в этом общем интеграле удается отделить переменную в одну сторону, а и в другую, то получим общее решение уравнения вида . Если не удается, то ответом может считаться общий интеграл.

При изучении конкретного явления, описываемого некоторым дифференциальным уравнением, требуется найти одно конкретное частное решение, описывающее данное явление. Дифференциальное уравнение же, как мы убедились, имеет бесконечно много решений (заключенных в формуле его общего решения). Поэтому для выделения нужного из них кроме самого уравнения необходимо привести дополнительное условие, позволяющее выделить нужное решение из бесконечного числа других решений. Например, для получения вида траектории полета пули кроме самого дифференциального уравнения (выражающего 2-й закон Ньютона для свободного полета пули данной массы под действием силы тяжести) необходимо дополнительно знать начальную скорость и начальное положение пули (от этого будет зависеть вид траектории). Для дифференциального уравнения первого порядка (1) это дополнительное условие обычно задается тем, что требуют, чтобы искомое решение уравнения (1) при заданном нами значении переменной давало бы заданное нами значение переменной . Задача нахождения одного конкретного решения уравнения , удовлетворяющего такому дополнительному условию, называется задачей Коши для этого уравнения. Форма записи задачи Коши следующая:

(3) .

Для решения задачи Коши сначала ищется общее решение дифференциального уравнения , а затем из дополнительного условия ищется то числовое значение параметра С, при котором выполняется это соотношение. Поскольку выполнение условия для функции на языке геометрии означает, что ее график проходит через точку с соответствующими координатами, то геометрический смысл задачи Коши (3) состоит в том, что ищется такое решение уравнения , чтобы соответствующая ему интегральная кривая этого уравнения проходила через заданную точку координатной плоскости.

Поскольку мы нашли (а точнее, угадали и проверили) общее решение только одного пока уравнения , то и примеры будут касаться только этого уравнения.

Пример 2. Построить интегральные кривые уравнения .

Р ешение. Напомним, что интегральные кривые дифференциального уравнения это графики решений этого уравнения. Поскольку (как мы ранее нашли) все решения уравнения заключены в формуле его общего решения , то нам и нужно построить графики этих функций при всех числовых значениях параметра . Известно (из пройденной ранее аналитической геометрии), что уравнениями вида задаются всевозможные прямые на координатной плоскости, проходящие через начало координат и не совпадающие с осью ординат . Поэтому все такие прямые и будут исчерпывать интегральные кривые этого уравнения. Поскольку таких прямых бесконечно много, то изобразим на рисунке лишь некоторые из них, соответствующие различным значениям параметра .

Если для этого уравнения будет поставлена задача Коши, то будет искаться то решение уравнения, для которого соответствующая ему прямая проходит через точку с заданными координатами .

Пример 3. Найти решение задачи Коши

(4) .

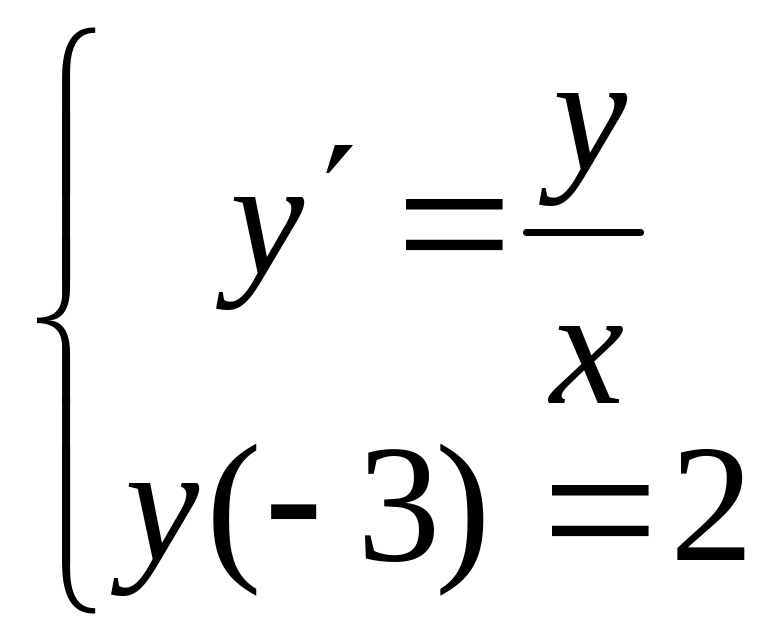Решение. Все решения данного уравнения получаются из его общего решения при различных значениях произвольной постоянной . При каком-то значении будет получаться и интересующее нас решение, удовлетворяющее условию (т.е. при дающее ). Найдем это значение , подставляя в выражение числа и и выясняя, при каком будет выполняться получившиеся равенство: , откуда . Подставляя полученное значение в общее решение , получим, что решением задачи Коши (4) является функция . Соответствующая интегральная кривая (точнее, прямая) изображена на рисунке.

Как же находить общие решения (или общие интегралы) дифференциальных уравнений? Точно так же, как есть неберущиеся интегралы (т.е. не выражающиеся через элементарные функции), так есть и нерешаемые дифференциальные уравнения (в том смысле, что их решение не может быть записано в элементарных функциях). Однако для некоторых классов уравнений есть четкие схемы нахождения их общего решения или общего интеграла. Каков же должен быть вид правой части в дифференциальном уравнении , чтобы оно принадлежало к одному из этих классов? И что это за схемы? О некоторых типах таких уравнений и схемах их решения пойдет речь ниже. Но сначала познакомимся с еще одной формой записи дифференциальных уравнений.