Замена переменной и интегрирование по частям в определенном интеграле

Самым простым методом вычисления неопределенных интегралов был так называемый метод непосредственного интегрирования, сводящийся к преобразованию подынтегрального выражения к сумме-разности элементарных функций из таблицы интегралов с некоторыми числовыми коэффициентами. Если же это не удавалось, то предлагались два специальных приема – замена переменной и интегрирование по частям. Ситуация с вычислением определенных интегралов в точности та же самая. Имеется практически точно такой же метод непосредственного интегрирования определенных интегралов, который от того же метода для неопределенных интегралов отличается лишь на последнем этапе − тем, что после сведения задачи к интегрированию «табличных» функций при их последующем интегрировании мы после выписывания соответствующей первообразной не приписываем дальше «+ С» (как при вычислении неопределенного интеграла), а, в соответствии с формулой Ньютона-Лейбница, вместо этого ставим вертикальную черту с пределами интегрирования и считаем соответствующую разность значений первообразной. Примеры вычисления определенных интегралов методом непосредственного интегрирования приведены в предыдущих параграфах. Если же этот метод неприменим, снова используются методы замены переменной и интегрирования по частям, которые тоже очень похожи на эти же методы для неопределенного интеграла с небольшими изменениями. Такими же остаются и рекомендации по конкретным типам замены в зависимости от вида подынтегральной функции, а также по классам функций, при интегрировании которых применяется интегрирование по частям. Формулы, описывающие эти методы для случаев неопределенного и определенного интегралов, также очень похожи. Однако имеется некоторая их специфика для определенного интеграла, которая будет отмечена ниже. Начнем с формулы замены переменной, формальное изложение которой выглядит достаточно громоздко.

Теорема. Пусть 1) Функция непрерывна на отрезке [a, b]. 2) Функция имеет непрерывную производную на отрезке [α, β]. 3) , . 4) Множество значений функции не выходит за отрезок [a, b] при изменении t на [α, β]. Тогда справедлива следующая формула замены переменной:

.

Доказательство теоремы несложно, проводится с помощью формулы Ньютона-Лейбница и формулы дифференцирования сложной функции. Приведенная формула замены переменной в определенном интеграле отличается от соответствующей формулы для неопределенного интеграла лишь наличием пределов интегрирования в каждом из интегралов. В отличие от формулы замены переменной в неопределенном интеграле, в данном случае нет необходимости в ответе переходить к старой переменной, так как в ответе получится число – значение определенного интеграла. После того, как замена сделана, мы можем "забыть", как выглядел исходный интеграл, и продолжать преобразования интеграла от функции с новой переменной. Именно на том, что к старой переменной возвращаться не приходится, мы и получаем экономию усилий при применении формулы замены переменной в определённом интеграле, по сравнению с тем, что получилось бы, если бы мы просто нашли первообразную (сделав ту же замену переменных, но в неопределенном интеграле) и применили формулу Ньютона - Лейбница. Однако возникает дополнительная работа по расчету новых пределов интегрирования α и β для новой переменной интегрирования t.

Правила для пересчетов пределов интегрирования следующие.

1. Если при замене переменной старая переменная выражена через новую в форме , то новый нижний предел α для новой переменной находится из условия , а новый верхний предел β из условия .

2. Если при замене переменной новая переменная выражена через старую в форме , то , а .

Советы о том, какая замена целесообразна для вычисления того или иного интеграла, − те же самые, что и при вычислении неопределённых интегралов, так что тут ничего нового изучать не придётся.    Итак, два основных отличия от замены переменных в неопределенном интеграле состоят в том, что в ответе теперь не нужен возврат к старой переменной, зато добавляется работа по пересчету пределов интегрирования α и β для новой переменной.  

Пример 1. Вычислить .

Решение. В предыдущей главе (посвященной неопределенным интегралам) в конце параграфа «Интегрирование некоторых иррациональных выражений» при интегрировании выражений, содержащих , предлагалась замена переменной вида . Такого же вида замену сделаем и сейчас, не забывая пересчитать пределы интегрирования α и β для новой переменной по приведенному выше правилу 1.

= {применим формулу понижения степени } = .

Итак, .

Пример 2. Вычислить .

Решение. Для неопределенных интегралов, содержащих переменную интегрирования только под знаком экспоненты , рекомендовалась замена переменной по формуле . Поэтому в данном примере надо бы сдеать замену переменной по формуле . Однако в данном случае решение будет короче, если сделать замену (так как именно такое выражение стоит под знаком корня в интеграле). Пересчет пределов интегрирования α и β для новой переменной выполняем по правилу 2.

. Итак, .

Рассмотрим теперь метод интегрирования по частям в определенном интеграле. По форме он почти не отличается от аналогичного метода для неопределенных интегралов.

Теорема. Пусть функции u(x) и v(x) имеют непрерывные производные на отрезке [a,b]. Тогда справедлива следующая формула интегрирования по частям:

(1) .

Напомним формулу интегрирования по частям для неопределенного интеграла, приведенную в параграфе «Интегрирование по частям» предыдущей главы:

(2) .

Видно, что отличия в формуле (1) от формулы (2) лишь в том, что интегралы справа и слева становятся определенными, а выражение заменяется на , что, как обычно, означает разность значений при и выражения слева от вертикальной черты. В том же параграфе предыдущей главы были приведены типы интегралов, для вычисления которых следует применять метод интегрирования по частям, а так же рекомендации, что при этом брать за , а что за . Все эти рекомендации справедливы и при вычислении определенных интегралов:

1. 2. 3. 4.

Пример 3. Вычислить .

Решение. Это второй из перечисленных выше типов интеграла, поэтому применяем формулу интегрирования по частям (1), беря в соответствии с рекомендацией за , а за :

. Итак, .

Пример 4. Вычислить .

Решение. Это интеграл первого из перечисленных выше типов при и , поэтому при применении формулы (1) делаем рекомендуемый выбор функций и :

{ учтем, что } .

Таким образом, .

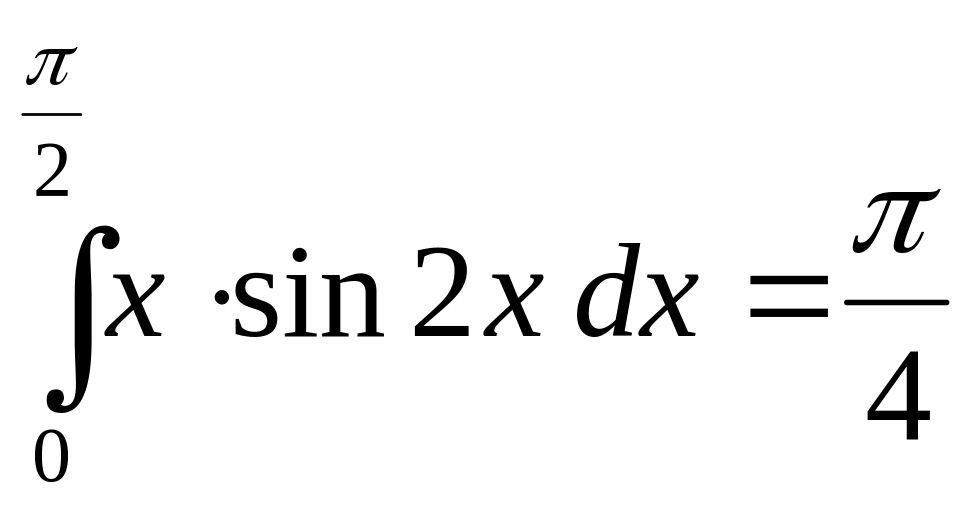Пример 5. Вычислить .

Решение. Представим интеграл в виде : . Теперь видно, что это интеграл третьего типа при (так как ), и . Применяем формулу (1):

{учтем, что , а } .

Итак, .