Дифференциальные уравнения второго порядка

В такие уравнения (согласно определению порядка дифференциального уравнения) искомая функция может входить вместе с производными до второго порядка включительно, причем наличие в уравнении второй производной обязательно. Кроме второй производной от искомой функции в уравнение второго порядка могут (но не обязаны) входить ее первая производная , сама искомая функция и ее аргумент . Снова будем рассматривать уравнения второго порядка, разрешенные относительно старшей (в данном случае второй) производной. Это уравнения вида

(1) ,

где под в правой части понимается функция трех переменных, выраженная формулой, содержащей , и . Попробуем теперь понять структуру решений такого уравнения и перенести основные понятия, которые были введены для уравнения 1-го порядка (решение, общее решение, задача Коши и т.д. ), на уравнения второго порядка (1). Аналогично ситуации с уравнением 1-го порядка, функция называется решением уравнения (1) на некотором числовом интервале , если при подстановке ее в уравнение вместо неизвестной функции получается верное тождество на этом интервале: . Аналогично, если функция является решением уравнения (1), то ее график называется интегральной кривой этого уравнения.

Попробуем понять структуру решений уравнения второго порядка, непосредственно найдя все решения какого-либо простейшего из них. В качестве примера рассмотрим уравнение

(2) .

В этом случае функция в (1) имеет простой вид и не содержит искомой функции и ее первой производной . Это уравнение можно решить непосредственно без всяких предварительных знаний о структуре решения уравнений второго порядка. Требуется найти функцию, вторая производная которой равна . Найдем сначала не саму искомую функцию, а ее производную . Поскольку вторая производная есть по определению производная от первой производной, то уравнение (2) может быть записано в виде . Таким образом, нам известна производная от функции . Как известно, по ее производной функция восстанавливается с помощью неопределенного интеграла, поэтому . Поскольку , то производной от искомой функции может быть (и будет!) только функция вида: при любом числовом значении произвольной постоянной (мы пишем , а не привычное , поскольку при дальнейшем решении появится еще одна произвольная постоянная, которую мы обозначим ). Итак, нам известен вид производной от искомого решения: . Снова восстанавливаем функцию по известной ее производной с помощью интегрирования: , где тоже произвольная постоянная, появившаяся после интегрирования. Таким образом, все решения уравнения (2) имеют вид

(3) ,

где и − произвольные числа (произвольные постоянные). Если вспомнить, то в формулу общего решения уравнения первого порядка входила только одна произвольная постоянная , но, как видно из приведенного примера, общее решение уравнения второго порядка должно содержать уже две произвольные постоянные и . Поэтому примем следующее определение: выражение вида , содержащее две произвольные постоянные и , называется общим решением уравнения второго порядка , если при любых (допустимых) числовых значениях С₁ и С₂ оно дает решение этого уравнения. Для уравнения , как мы только что выяснили, общим решением будет выражение .

Поговорим о задаче Коши для уравнения второго порядка (1). Если надо из всех решений этого уравнения выделить одно конкретное решение, то необходимо определить конкретные значения уже двух произвольных постоянных С₁ и С₂, входящих в формулу общего решения. Для их определения нужны уже два дополнительных условия ( для уравнения 1-го порядка, напомним, достаточно было одного дополнительного условия вида для нахождения значения одной произвольной постоянной С, содержащейся в формуле общего решения). Поэтому в качестве дополнительных условий при решении задачи Коши для уравнения (1) задают не только значение самой искомой функции в некоторой точке, но и значение ее производной в этой же точке. Таким образом, Итак, задачей Коши для уравнения второго порядка (1) называется задача нахождения такого решения этого уравнения, которое при заданном нами значении принимает заданное нами значение , а его производная в этой же точке принимает заданное нами значение . Запись задачи Коши выглядит следующим образом:

(4) .

Пример 1. Найти решение следующей задачи Коши: .

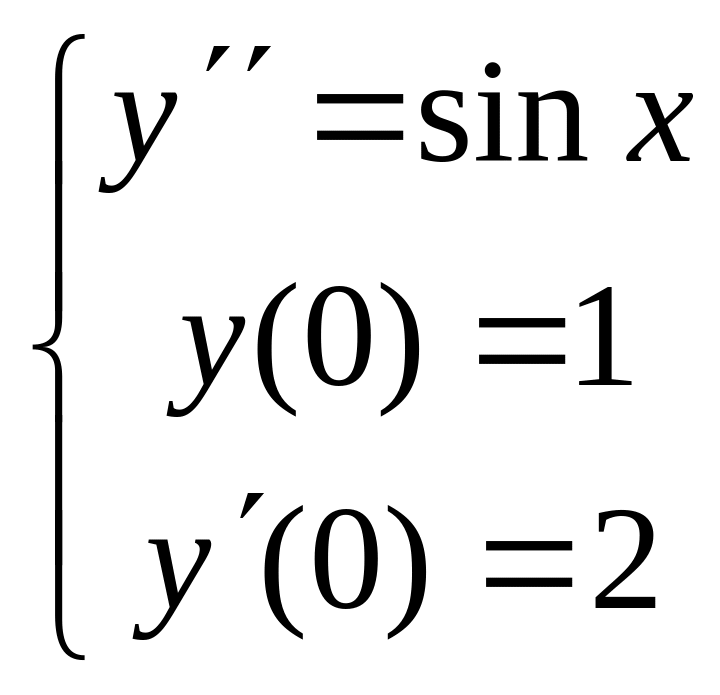Решение. Наш пример имеет вид задачи Коши (4) с параметрами: , и . Мы уже нашли вид общего решения предложенного уравнения , содержащего все его решения при различных значениях произвольных постоянных и : . Найдем теперь такие числовые значения постоянных и , при которых функция будет удовлетворять дополнительным условиям: и . Условие говорит о том, что при подстановке в выражение для функции должно получиться число 1: , т.е. (с учетом, что ). Таким образом, значение одной произвольной постоянной мы уже определили. Подставляем в формулу для общего решения , получаем функцию . Эта функция (при любом значении ) удовлетворяет как заданному уравнению , так и первому дополнительному условию . Найдем теперь значение произвольной постоянной , при котором эта функция удовлетворит и второму дополнительному условию , т.е. при подстановке в выражение для производной этой функции должно получиться число 2. Поскольку у нас пока нет выражения для производной функции , то найдем его: , т.е. . Подставляем в него − должны получить : . Отсюда (с учетом ) , т.е. . Подставляя найденное значение в выражение , получаем, что решением исходной задачи Коши является функция .