Линейное уравнение

Продолжаем изучение уравнений, для которых известен алгоритм их решения. Линейными дифференциальными уравнениями (первого порядка) называются уравнения вида

(1) ,

где и − непрерывные на некотором интервале функции. Если , то уравнение (1) называется однородным уравнением, а иначе – неоднородным уравнением. Наиболее просто ищется общее решение однородного уравнения:

(2) .

Действительно, после перенесения второго слагаемого в правую часть получаем уравнение , которое, очевидно, является уравнением с разделяющимися переменными (правая часть представляется в виде произведения функции, зависящей только от , и функции, зависящей только от ). По пройденному алгоритму решения таких уравнений сначала умножаем обе его части на , учитывая, что слева : . Затем делим обе части уравнения на (при этом теряем решение , но потом его восстановим): . Теперь «навешиваем» интегралы на правую и левую части: . При вычислении интеграла по не пишем «+С»: , а при вычислении интеграла по добавка «+С» обязательно появится, которую мы явно выпишем. Поэтому приходим к общему интегралу , где уже под интегралом справа понимаются не все, а какая-либо одна первообразная от , поскольку произвольная постоянная уже явно выписана в формуле для общего интеграла. Мы получили общий интеграл такого вида, из которого мы раньше научились получать и общее решение. Напомним, что одно из утверждений леммы в параграфе «Уравнения с разделяющимися переменными» звучало так: «Общий интеграл вида (где − произвольная функция) дает общее решение ,где − произвольная постоянная, не равная 0 ( )». В полученном общем интеграле роль играет , а потому общее решение может быть записано в виде , где . Однако при из этой формулы получаем потерянное ранее решение , поэтому ограничение можно убрать! Итак, мы доказали, что справедлива следующая

Теорема 1. Общее решение однородного линейного уравнения (2) имеет вид

(3) ,

где под интегралом в экспоненте справа понимается какая-либо одна первообразная от (т.е. после вычисления «+С» писать не надо), а − произвольная постоянная.

Пример 1. Найти общее решение уравнения .

Решение. Это линейное однородное уравнение вида (2), для которого . Для того, чтобы выписать его общее решение по формуле (3), вычислим значение показателя степени у экспоненты в этой формуле: (напомним, что «+С» писать не надо). Тогда по формуле (3) общее решение этого уравнения имеет вид , где С – произвольная постоянная.

Рассмотрим теперь неоднородное линейное уравнение (1). Вид общего решения этого уравнения устанавливает следующая

Теорема 2. Общее решение неоднородного линейного уравнения (1) имеет вид

(4) ,

где

(5) ,

причем при вычислении интегралов, входящих в (4) и (5) снова требуется лишь одна первообразная (т.е. «+С» писать не надо) , а − произвольная постоянная.

Отметим, что если в уравнении (1) (т.е. уравнение на самом деле является однородным), то формулы (4) и (5) переходят в формулу (3) – общее решение однородного уравнения (что и должно быть). Таким образом, для получения общего решения неоднородного уравнения (1) по формулам (4), (5) необходимо предварительно вычислить два интеграла: и .

Пример 2. Найти решение задачи Коши: .

Решение. Таким образом, необходимо найти такое решение уравнения

(6) ,

которое при принимает значение . Найдем сначала все решения уравнения (6), а затем выберем из них нужное. Это линейное неоднородное уравнение вида (1), в котором , а . Для нахождения его общего решения по формулам (4), (5) вычислим предварительно интегралы и . Первый интеграл: . Тогда из (5): . Тогда второй интеграл: {вносим число 5 под знак дифференциала} . Подставляя полученные значения интегралов в формулы (4) и (5), получим общее решение уравнения (6): . Для упрощения полученного выражения раскроем скобки: . Итак, общее решение уравнения (6) имеет вид

(7) .

Найдем теперь такое числовое значение произвольной постоянной С в (7), при котором полученная функция при принимает значение . Подставляя в (7) и , получаем следующее уравнение для нахождения нужного значения С: или или . Отсюда . Подставляя это значение в (7), получаем следующее решение исходной задачи Коши: .

Пример 3. Найти общее решение уравнения : .

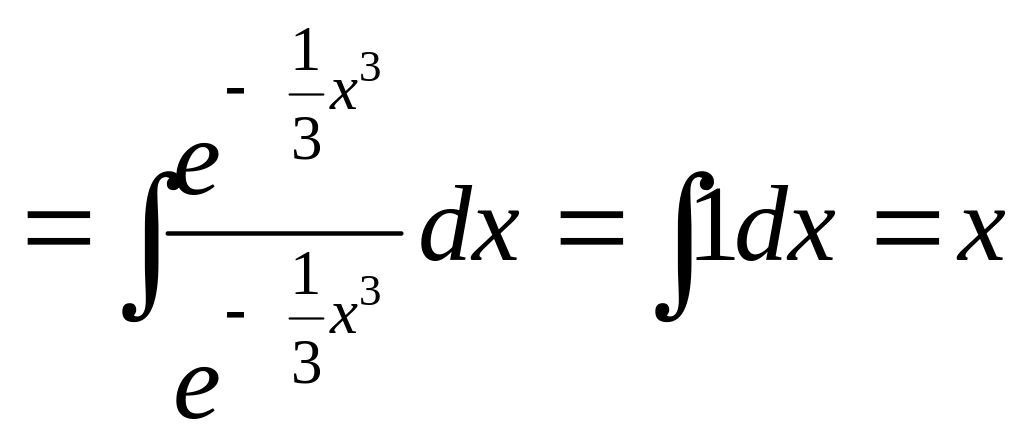Решение. Это линейное неоднородное уравнение вида (1), в котором , а . Для нахождения его общего решения по формулам (4), (5) вычислим необходимые интегралы: . Тогда из (5): , а . Подставляя полученные значения интегралов в формулы (4) и (5), получим общее решение уравнения: .

К линейному уравнению сводится так называемое уравнение Бернулли. Это уравнение вида

(8) ,

где и − непрерывные на некотором интервале функции. Показатель степени в правой части (8) может быть любым действительным числом, кроме и . При уравнение (8) переходит в обычное линейное уравнение , а при очевидными преобразованиями оно приводится к уравнению с разделяющимися переменными . Непосредственной подстановкой в уравнение (8) легко убедиться, что для функция обязательно будет одним из его решений. Для решения уравнения Бернулли будем искать такую вспомогательную функцию , чтобы функция

(9)

была бы решением уравнения (8). Тогда после подстановки (9) в (8) для определения функции получается линейное уравнение.

Пример 4. Найти общее решение уравнения

(9) .

Решение. Это уравнение Бернулли вида (8) с параметром . Согласно (9), будем искать такую вспомогательную функцию , чтобы функция была бы решением уравнения (9). Подставим функцию в уравнение (9), предварительно найдя выражение для производной: . После подстановки и в (9), получаем: . После умножения обоих частей этого уравнения на , получаем уравнение на вспомогательную функцию :

(10) .

Это линейное уравнение, общее решение которого ранее уже было найдено в примере 3 (убедитесь!): . Учитывая, что искомая функция связана с функцией соотношением , получаем общее решение исходного уравнения

(11) .

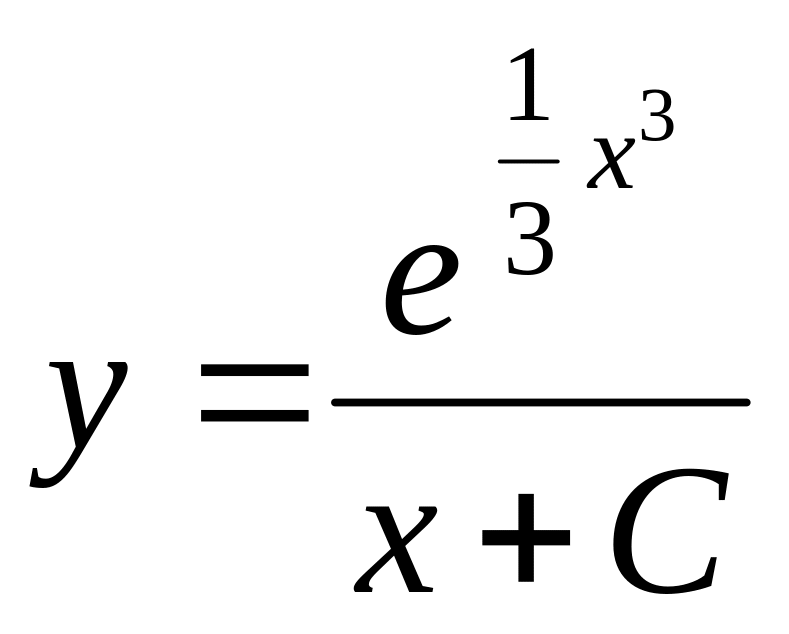Для того, чтобы получить все решения исходного уравнения, нужно к (11) добавить решение , которое, как отмечалось выше, является решением любого уравнения Бернулли (8) при , но не получается из (11) ни при каком значении произвольной постоянной С.